ПРИНЦИПЫ ЛАЗЕРОВ

ПУЧКИ С ЧАСТИЧНОЙ ПРОСТРАНСТВЕННОЙ КОГЕРЕНТНОСТЬЮ

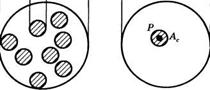
Расходимость электромагнитной волны с частичной пространственной когерентностью заведомо больше, чем пространственно-когерентной волны, имеющей такое же распределение интенсивности. Это можно понять, напри­мер, из рис. 1.6: если волна не является пространственно-когерентной, то вторичные волны, излученные с ее плоскости поперечного сечения, не долж­ны больше находиться в фазе и волновой фронт, образованный вследствие дифракции, должен иметь большее значение расходимости по сравнению с той, которая получается из выражения (11.4.6). Строгое рассмотрение этой задачи (т. е. задачи о распространении частично-когерентных волн) выходит за рамки обсуждения настоящей книги, и ознакомиться с данным вопросом более детально можно в работе [3]. В рамках этого раздела данное рассмотре­ние ограничится лишь изучением относительно простого случая — пучка диаметром!) (рис. 11.7а), который состоит из множества пучков (показан­ных на рисунке в виде заштрихованных кружков) меньшего диаметра й. Предположим, что каждый из этих пучков меньшего диаметра является ди - фракционно-ограниченным (т. е. пространственно когерентным). Тогда, если составляющие пучки взаимно некоррелированы, расходимость всего пучка в целом будет равна Если бы такие пучки были коррелированны­

Ми, то расходимость была бы равна = (ЗА./1). В последнем случае множество пучков можно представить в виде маленьких антенн, каждая из которых излучает синхронно с остальными.

После этого простого примера можно рассмотреть общий случай, когда пространственно-когерентный пучок имеет заданное распределение интен­сивности по диаметру!) поперечного сечения и область когерентностиАс в заданной точке Р (рис. 11.76). По аналогии с предыдущим примером нетруд­но понять, что в этом случае

% = ^/вс,

Где Вс — диаметр области когерентности, ар — числовой коэффициент по­рядка единицы, значение которого зависит как от конкретного распределе­ния интенсивности, так и от способа, каким определялись величины 0<* и Д.. Итак, понятие направленности тесным образом связано с понятием простран­ственной когерентности.

Б

Рис. 11.7 Примеры, иллюстрирующие различные свойства расходимости когерентной и частично-когерентной волн:

А) пучок диаметром Б представляет со­бой суперпозицию множества меньших по размеру когерентных пучков диамет­ром с?; б) пучок диаметром Б и область когерентности в точке Р.