ПРОСТРАНСТВЕННО-ЗАВИСИМАЯ МОДЕЛЬ
Рассмотрим случай, когда распределение моды в резонаторе и скороспУ накачки являются пространственно зависимыми. В данном случае инверсиД населенностей оказывается также пространственно зависимой и, таким стразом, скоростные уравнения становятся более сложными. Таким образов, в данном разделе будут рассмотрены наиболее важные результаты, а более^е- тальное их описание можно найти в приложении Д. Предположим, что распределение поля в резонаторе обладает цилиндрической симметрией, и пусть величина и обозначает амплитуду поля заданной моды, нормированную на ее максимальное значение. Для простоты представим, что величина и не зависит от продольной координаты г резонатора, тогда как скорость накачки будем считать зависящей как от радиальной, так и от продольной координаты, т. е. Ир = Rp(r9 г).
Поскольку здесь рассматриваются пороговые условия, в приложении Д будет показано, что выражение (7.3.2) рассматривается для среднего значения инверсии ЛГ, т. е.:
(Юс в (У/а0> (7.3.19)
Где усреднение ведется по распределению квадрата амплитуды поля [см. также выражение (6.3.17)], а именно:
/
|
(N)- |
![]() PV | и |2 dV /1 и |2 dV (7.3.20)
PV | и |2 dV /1 и |2 dV (7.3.20)
а
И интегрирование ведется по всему объему активной среды. В каждой точке активной среды (ниже порога генерации или близко к нему) должно соблюдаться условие равновесия между числом атомов, возбуждаемых под действием накачки, и числом спонтанно релаксирующих атомов, т. е. Rp(r, г) = = N(r, г)/т. При достижении порога генерации имеем следующее:
<Л)с=Ик = JL (7.3.21)
У т gIt
Где (Rp) обозначает усреднение величины Rp (г, г) по распределению квадрата амплитуды поля [см. выражения (6.3.8) (7.3.19)].
После достижения порога генерации, при условии d§/dt = 0, находим, что среднее значение усиления равняется полным потерям, т. е.:
Ol{N)о - у - gI(N)c. (7.3.22)
Таким образом, согласно данному выражению среднее значение инверсии (N)0 достигает порогового значения и остается на этом уровне после превышения порога (см. рис. 7.3).
Для расчета пороговой (Рел) и выходной (Pout) мощности лазера необходимо знать пространственные распределения величин и2 и Rp. Предположим, что генерация осуществляется на одной моде ТЕМ00. Для этого случая запишем:
| и |2= ехр[-(2г2 /м>о)]. (7.3.23)
Это означает, что: 1) поперечный размер пучка не зависит от координаты 2 и равен размеру пучка в перетяжке (w0); 2) профиль стоячей волны моды можно не учитывать (в качестве сравнения см. выражение (6.3.9)).
Для распределения Rp (г, г) рассматриваются два случая: 1) накачка однородна, т. е. Rp = const; 2) профиль накачки является гауссовым, как в случае продольной накачки, например лазерными диодами. В этом случае имеем
Rp(r, z) = Сехр[-2(г2 /и;2)]ехр[-(аг)],
Где С — константа, пропорциональная полной входной мощности накачки (см. выражение (6.3.7)).
Рассмотрим вначале случай однородной накачки, которая обеспечивается либо лампой, либо электрическим разрядом. Далее, используя выражение (6.2.6) или (6.4.26), получаем:
Где а — радиус цилиндрической среды. Теперь рассмотрим стержень с боковой поверхностью, выполненной в виде оболочки (см. раздел 6.3.3), где активная среда заключена только в центральной области 0 ^ г ^ а стержня, тогда как вне этого диапазона (т. е. при г > а) в стержне отсутствуют какие-либо примесные атомы. В этом случае усечением пучка вследствие ограниченной апертуры активной среды можно пренебречь. Таким образом, уравнение (7.3.23) можно решать для области 0 < г < оо, принимая во внимание, что Rp = const для 0^г^аиЛр=0 для г > 0. Для определения среднего значения Rp подставим выражение (7.3.24) в (7.3.21) и применим затем соотношение (7.3.23). В этом случае получаем выражение для пороговой мощности Pth, которое имеет тот же вид, что и соотношение (6.3.22), если параметр г)р заменить на гр1. Далее расчет выходной мощности выполняется по алгоритму, приведенному в приложении Д; здесь будут рассмотрены лишь конечные результаты. Определим нормированную мощность накачки х в виде
X = Pp/Pmth, (7.3.25)
|
(7.3.26) |
![]() Где Pmth — минимальное значение порога генерации, которое имеет место при w0 <С а и которое определяется, согласно выражению (6.3.22), как
Где Pmth — минимальное значение порога генерации, которое имеет место при w0 <С а и которое определяется, согласно выражению (6.3.22), как
|
Ґ Y |
HVmp ^ |
F па2 > |
|
1 ^ J |
1 J |
|
Rmth |
Также зададим нормированную выходную мощность у в виде
У = Роиг/Р8, (7.3.27)
Где Р8 — мощность, при которой активная среда насыщается. Данный пара-
Метр определяется как
_ У о nwfi,
Ps =2—~2~ *' (7.3.28)
|
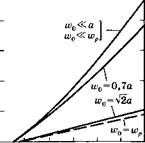
Нетрудно видеть, что соотношение, связывающее нормированную выходную мощность у и величину ху характеризующую превышение накачки над порогом, значительно отличается от выражения, полученного с помощью пространственно-независимой модели скоростных уравнений (см. формулу (7.3.9)).1 Для сравнения, на рис. 7.9 (сплошная кривая) приведена зависимость нормированной выходной мощности у от нормированной мощности накачки х для случаев: ии0 «а, ш0 = 0,7а и ьи0 = а[2. Можно заметить, что зависимость у от х имеет теперь нелинейный характер, причем производная с1у/с1х возрастает с увеличением параметра х. Чтобы понять такой характер поведения данной зависимости, рассчитаем дифференциальный КПД г)з = йРоШ/йРр = (Р8/Рпцк)(йу/йх), используя выражения (7.3.25) и (7.3.27). С помощью выражений (7.3.26) и (7.3.28) нетрудно убедиться, что величина г)** может быть записана в виде выражения (7.3.14), если принять уя = Нх/кутр и определить эффективность заполнения активной среды т)г как |
|
Сплошные кривые отображают случай неоднородной накачки стержня радиусом а для нескольких значений поперечного размера перетяжки м>0моды. Пунктирная кривая приведена для случая гауссова профиля накачки с размером пучка и)ру при котором ю0 = и)р. |
|
Мощности у от нормированной мощности накачки х для лазера, генерирующего на моде ТЕМт: |
|
Зависимость нормированной выходной |
|
Рис. 7-9 |
|
(7.3.31) |
|
В случае поперечной накачки лазерными диодами (однородная накачка) для дифференциального КПД получается такое же выражение, с той лишь разницей, что теперь rjs = hv/hvp. Следует отметить, что при р 0, т. е. когда w0 <с а, имеем (dy/dx) = 2 для у -» 0 (х —> 0), и тогда эффективность заполнения активной среды определяется как r)f = (tiWq /па2). Также необходимо отметить, что поскольку (dy/dx) возрастает с увеличением х, то эффективность заполнения будет также возрастать с увеличением х. Чтобы понять это, рас- |
|
(ли>о /2) dy па2 dx |
|
2 4 6 8 10 12 |
|
Х |
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
![]()
![]()
![]()
|
Рис. 7.10 График зависимости эффективности заполнения активной среды от нормированной мощности х: |
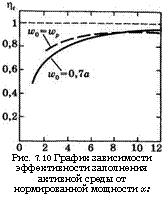
Смотрим в качестве примера случай, когда ю0 = = 0,7а. Зависимость от х для этого случая приведена на рис. 7.10 (сплошная кривая). Начиная со значения гг * 0,97(ю0/а)2 « 0,473, при небольших значениях мощности параметр гг растет и стремится к единице, когда х 1. Такое поведение можно объяснить тем, что энергия возбужденного атома может уменьшаться либо за счет процессов вынужденного излучения, либо за счет спонтанных переходов. Таким образом, при низких уровнях входной мощности, т. е. когда х->19 вблизи центральной области пучка (где интенсивность пучка высокая) преобладает вынужденное излучение, тогда как ближе к периферии пучка преобладает спонтанное излучение или спонтанные переходы. При больших значениях х, т. е. когда мощность пучка возрастает, вынужденное излучение начи - сплошная кривая отображает случай неоднородной накачки, пунктирная кривая приведена для случая гауссова профиля накачки.
Нает преобладать на большей части профиля
Накачки и, следовательно, для большей части возбуждаемых атомов. В конечном счете, при очень высоких уровнях мощности практически все возбужденные атомы будут участвовать в вынужденных переходах, т. е. = 1, и в этом случае весь профиль пучка накачки будет задействован в генерации [6].
 При использовании накачки лазерными диодами можно обеспечить значительное превышение мощности накачки над пороговым значением, и было бы полезно рассмотреть этот случай при изучении поведения зависимости г|*
При использовании накачки лазерными диодами можно обеспечить значительное превышение мощности накачки над пороговым значением, и было бы полезно рассмотреть этот случай при изучении поведения зависимости г|*
|
А б
|
(Щ/а) (и’о^Г
Рис. 7.11
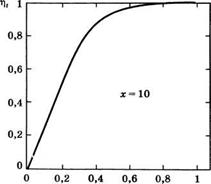
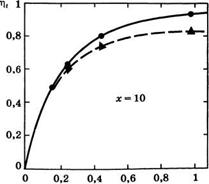
А) График зависимости эффективности заполнения г), активной среды от параметра (ш0/а)2 при нормированной мощности накачки х - 10 для случая неоднородной накачки (ы;0 — поперечный размер моды, а — радиус стержня), б) Зависимость т|, от параметра (^о/ы'р)2 при нормированной мощности накачки х = 10 для случая гауссова профиля накачки (здесь юр — размер пятна профиля накачки):
Кружками обозначен график для четырехуровневого лазера, треугольниками — для квази-трехуровневого лазера при В = авЛ^/у = !•
От параметра (ю0/а)2 для больших значений х. График такой зависимости для случая х = 10 приведен на рис. 7.11а. Из рисунка видно, что для получения значений г|* > 90% необходимо иметь ю0 > 0,66а, а для ьи0 = 0,7а достигается значение эффективности заполнения более 94%. Однако для более традиционных лазерных систем (со стержнем без оболочки) увеличивать и дальше поперечный размер пучка оказывается невыгодно, поскольку это приводит к значительному росту дифракционных потерь вследствие ограниченной апертуры стержня.
|
К |
![]()
|
![]() Для гауссова профиля пучка накачки вычисления проводятся аналогичным образом, см. также приложение Д. Здесь снова определяется нормированная выходная мощность как величина у, см. выражение (7.3.27), где величина Р8, как и раньше, задается отношением (7.3.28). Определим нормированную мощность накачки через х> см. выражение (7.3.25), где Ртгн представляет в этом случае минимальное пороговое значение для гауссова профиля пучка накачки и находится из выражения (6.3.20), когда ю0 <С юр. Таким образом, для Ртгн получаем:
Для гауссова профиля пучка накачки вычисления проводятся аналогичным образом, см. также приложение Д. Здесь снова определяется нормированная выходная мощность как величина у, см. выражение (7.3.27), где величина Р8, как и раньше, задается отношением (7.3.28). Определим нормированную мощность накачки через х> см. выражение (7.3.25), где Ртгн представляет в этом случае минимальное пороговое значение для гауссова профиля пучка накачки и находится из выражения (6.3.20), когда ю0 <С юр. Таким образом, для Ртгн получаем:
Рщгк =|
(7.3.32)
Соотношение между параметрами у их задается следующим выражением:
|
(7.3.33) |
|
У* |
Где 8 = (ю0/юр)2. И хотя это выражение отличается по форме записи, оно полностью согласуется с первоначальным представлением, которое было выведено Моултоном [13]. Для ю0 иор имеем 8 -» 0, так что выражение (7.3.33) дает такой же результат, что и отношение (7.3.29) (когда и>0 а, т. е. когда Р -> 0). Таким образом, график зависимости у от х имеет такой же вид, как и в случае однородной накачки (см. рис. 7.9). Действительно, для очень маленьких значений поперечного размера пучка не существует разницы между однородной накачкой и накачкой с гауссовым профилем распределения. Для ю0 = юр имеем 8 = 1.
Интегрируя уравнение (7.3.33), получаем:
|
(7.3.34) |
1-
У
График зависимости описываемый выражением (7.3.34), представлен на рис. 7.9 пунктирной линией. Здесь можно снова рассчитать дифференциальный КПД как г|в = (1Роиг/йРр = (Р8/Ртгк)(<1у/<1х) и убедиться, что параметр г8 может быть выражен через соотношение (7.3.14), где, как и в случае с поперечной накачкой лазерными диодами, г|9 — к/Нр и где теперь
(7.3.35)
Я ы>£ йх
Зависимость гг от параметра х при ьи0 = ьир9 определяемая выражениями (7.3.34) и (7.3.35), представлена на графике рис. 7.10 пунктирной линией. Рост кривой в этом случае имеет тот же физический смысл, что и в случае однородной накачки. Необходимо отметить, что для относительно больших значений х (х > 7) эффективность заполнения среды для этих двух случаев оказывается приблизительно одинаковой. График зависимости тг от параметра (IVо/юр)2 для х — 10 показан на рис. 7.116. Точками на графике обозначены результаты, взятые из источника [13], тогда как кривые отображают результат интерполяции этих точек. Сравнивая графики на рис. 7.11а и б, можно видеть, что рост зависимости г|* от параметра (и)0/и>р)2 оказывается более медленным, чем в случае однородной накачки. Это связано с более низким значением скорости накачки на краях гауссова профиля по сравнению с однородным распределением накачки.
Из графиков на рис. 7.116 видно, что для достижения более высоких значений т],, например 94%, достаточно иметь ю0 « и)р9 хотя это менее выгодно с точки зрения увеличения поперечных размеров лазерного пучка. Действительно, если гг в этом случае увеличивается незначительно, то пороговая мощность накачки Р^, которая пропорциональна величине (м;§+м;|), (см. выражение (6.3.20)), может возрасти существенно. Таким образом, при больших значениях х условие и>0 « юр (также называемое условием согласования мод) может считаться более или менее оптимальным. Пунктирная линия на рис. 7.9 отображает зависимость выходной мощности для данного случая при определенной мощности накачки. Если сравнить данную кривую с зависимостью, при которой ю0 = 0,7а, может возникнуть ошибочное ощущение, что для заданного значения х и для одного и того же размера пятна ю0 в пучке выходная мощность, полученная при использовании гауссова профиля накачки, оказывается меньше, чем при использовании однородной накачки. Однако при рассмотрении этих двух случаев накачки необходимо проводить сравнение не только для равных размеров пучка, но и для одинаковой области накачки, т. е. для (пи>2 /2) = па2. Если теперь рассмотреть случай ю0 = юр (для гауссовой накачки), и если принять равными размеры пятна в моде для этих двух случаев, то будет иметь место (пи% /2) = па2. Таким образом, для однородной накачки кривая, которую необходимо взять в качестве сравнения, должна рассматриваться для размера перетяжки ьи0 = 42а. Этот график также приведен на рис. 7.9, и здесь нетрудно видеть, что пунктирная кривая (гауссов профиль накачки) и сплошная кривая (однородная накачка) практически совпадают. Следует отметить, что кривая с параметром и>0 -[2а приведена лишь в качестве сравнения, поскольку для реальной активной среды (стержень без оболочки) данная ситуация приводила бы к значительному увеличению дифракционных потерь вследствие ограниченной апертуры активной среды.
До сих пор при рассмотрении данной темы характер моды стоячей волны не учитывался, т. е. величина и2 описывалась выражением (7.3.23), а не (6.3.9). Это справедливо для однонаправленных кольцевых резонаторов (см. рис. 5.4а), тогда как для большинства других случаев, например для резонаторов с двумя зеркалами, при генерации одной продольной моды формируется характерная пространственная картина стоячей волны.[31] Для моды с равномерным поперечным распределением влияние характера профиля распределения стоячей волны на выходную мощность было рассмотрено Касперсоном [6]. Полученный результат можно представить в виде пятого множителя в правой части выражения (7.3.14), которое описывало величину дифференциального КПД. Можно обозначить этот множитель как продольный коэффициент использования распределения накачки Т1г, или продольную эффективность. Вблизи порога генерации это значение составляет г|/ = (2/3) = 0,666 и увеличивается до значения, например, = (8/9) = 0,89 при десятикратном превышении порога.
Физический смысл величины г|{ примерно такой же, как и г|,, а именно: после достижения порога генерации атомы, находящиеся в области пучности стоячей волны, распадаются преимущественно за счет вынужденных процессов, тогда как атомы, расположенные вблизи узлов стоячей волны, участвуют в спонтанных переходах. Таким образом, при увеличении параметра ху т. е. при увеличении плотности энергии, большая часть атомов, которые располагаются вблизи максимумов амплитуды поля, распадаются в большей степени за счет вынужденных процессов, и продольная эффективность возрастает.
В заключение данного раздела отметим, что если принимать во внимание пространственную зависимость уравнений, задача становится более сложной. Однако выражения для пороговой инверсии населенности и пороговой скорости накачки остаются идентичными тем, которые получены при рассмотрении пространственно-независимой модели, если использовать средние значения (Ы)с и (.Е)с. Следует также отметить, что, как показано в разделе 6.3.3, данный результат также является подходящим, если учитывать пространственную картину стоячей волны в моде. С другой стороны, выражение для выходной мощности, как функции величины превышения накачки над порогом, усложняется. Тем не менее, что касается величины дифференциального КПД, данные результаты являются простыми и понятными, и они могут быть напрямую связаны с результатами, полученными в рамках пространственно-независимой модели.
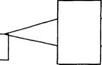
Пример 7.4. Пороговые условия и выходная мощность Nd:YAG лазера с продольной накачкой лазерными диодами. В качестве примера рассмотрим схему лазера, приведенную на рис. 7.12, в которой используется Nd: YAG стержень длиной 1 см. Для продольной накачки стержня используется массив из лазерных диодов, ширина массива — 100 мкм, длина волны излучения накачки составляет 805-808 нм [15]. Согласующая оптика состоит из собирающей линзы с фокусным расстоянием 6,5 мм и числовой апертурой 0,615; пары анаморфотных призм с кратностью 4х и линзы с фо-
|
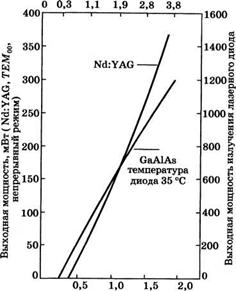
Рис. 7.12 Схема экспериментальной установки Ш:УАО лазера с продольной накачкой массивом лазерных диодов (согласно работе [15]) Электрическая входная мощность, Вт
Электрический ток, А Рис. 7.13 Зависимость выходной мощности NdrYAG лазера (схема, рис. 7.12) и выходной мощности излучения накачки от электрического тока, протекающего через массив лазерных диодов (согласно работе [15]) |
|
Охлаждение |
![]()
|
Согласующая Оптика |
![]()
|
Входное излучение 0,805-0,808 мкм |
![]()
|
Массив Лазерных Диодов |
![]()
|
Выходное зеркало, коэффициент отражения 95%, радиус 10 см
|
 Кусным расстоянием 25 мм для фокусировки излучения накачки на стержне (см. рис. 6.12). В данном случае резонатор NdrYAG лазера формируется из плоского зеркала, напыленного на входной торец стержня и выходного зеркала радиусом 10 см, коэффициент отражения которого составляет 95%; расстояние между зеркалами составляет приблизительно 5,5 см. Через плоское зеркало в стержень передается около 93% мощности накачки. При такой геометрии перетяжка моды ТЕМ00 формируется на плоском зеркале, и размер пятна в перетяжке может быть рассчитан как w0 « 130 мкм (при этом влиянием тепловой линзы в стержне можно пренебречь). Такой размер
Кусным расстоянием 25 мм для фокусировки излучения накачки на стержне (см. рис. 6.12). В данном случае резонатор NdrYAG лазера формируется из плоского зеркала, напыленного на входной торец стержня и выходного зеркала радиусом 10 см, коэффициент отражения которого составляет 95%; расстояние между зеркалами составляет приблизительно 5,5 см. Через плоское зеркало в стержень передается около 93% мощности накачки. При такой геометрии перетяжка моды ТЕМ00 формируется на плоском зеркале, и размер пятна в перетяжке может быть рассчитан как w0 « 130 мкм (при этом влиянием тепловой линзы в стержне можно пренебречь). Такой размер
пятна в пучке накачки обеспечивает хорошее согласование для лазерной моды ТЕМ00. Выходные характеристики лазера приведены на рис. 7.13. Пороговая мощность накачки составляет Р, Л «75 мВт. При оптической мощности накачки Рр = 1,14 Вт достигается выходная мощность РоШ = 370 мВт. При такой выходной мощности измеренное значение дифференциального КПД для оптической накачки составляет г|5 » 40%.
Чтобы сравнить пороговую мощность накачки с ожидаемым значением, предположим, что поперечное распределение пучка накачки описывается приблизительно гауссовой функцией, и предположим, что и>р~юо = 130 мкм. Из выражения (6.3.22), принимая Нур = 2,45 • 10~19 Дж, ое = 2,8 • 10-19 см2ит = 230 мкс, получаем (у/гр) « 3,7 • 10~2. Для коэффициента пропускания 5% выходного зеркала получаем у2 » 5 • 10-2, далее, полагая, что внутренние потери за проход составляют уь = 0,5 • 10-2, получаем у = уг + (у2/2) = 3 • 10-2. Исходя из рассчитанного значения у/гр9 далее получаем величину гр « 81%, которая включает в себя суммарный коэффициент пропускания согласующей оптики, а также пропускание плоского зеркала для указанной длины волны излучения накачки. Следует отметить, что эффективность поглощения излучения накачки лазерным стержнем за один проход, описываемая выражением г|а = {1-ехр [-(а/)]}, может быть приравнена единице при среднем значении коэффициента поглощения ~6 см-1 в полосе длин волн 805-808 нм (см. рис. 6.8а) для стержня длиной 1= 1 см. Теперь можно сравнить измеренное значение дифференциального КПД с ожидаемым значением. Поскольку пороговая мощность при юр ж ю0 составляет 75 мВт, то минимальная пороговая мощность, которая имеет место при —» 0, должна составить половину этого значения, т. е. РшН * 38 мВт. Таким образом, при входной мощности
1, 14 Вт имеем х « 30. Для этого значения х, из уравнения (7.3.34), находим у = 26, а из выражения (7.3.35) получаем г|*« 0,97. Далее имеем Л с = (Уг/У) = 0,83 и цд = (807/1060) = 0,76. Таким образом, ожидаемое (расчетное) значение дифференциального КПД для оптической накачки составляет г|8 = ЛрЛсПгЛд = 0,49, что достаточно хорошо согласуется с измеренным значением. Следует отметить, что продольная эффективность здесь не принимается во внимание, поскольку лазер генерирует на многих продольных модах, вследствие чего суммарная пространственная картина стоячих волн этих мод формирует достаточно равномерное распределение плотности энергии вдоль лазерного стержня. Согласно выражениям (7.3.27) и (7.3.28), ожидаемое значение выходной мощности, при мощности на входе 1,14 Вт, составляет РоШ = уР8 = 500 мВт, т. е. несколько больше экспериментального значения. Это расхождение может быть связано с тепловыми эффектами в лазерном стержне, которые при больших значениях мощности накачки приводят к росту потерь и уменьшению размера пятна ю0.
Следует отметить, что указанное выше значение эффективности 40% имеет отношение только к оптической эффективности. Для получения полного дифференциального КПД лазера, учитывающего электрическую накачку массива лазерных диодов, необходимо умножить оптическую эффективность на значение г|г эффективности преобразования электрической накачки в оптическую. Из рис. 7.13 находим г|г « 29%, таким образом, значение полного дифференциального КПД составляет около 11,6% .