ПРОСТРАНСТВЕННО-НЕЗАВИСИМАЯ МОДЕЛЬ
В разделе 7.2 были рассмотрены скоростные уравнения для четырехуровневой схемы лазера, предполагалось, что время жизни нижнего лазерного уровня является очень коротким. Прежде чем приступить к подробному рассмотрению непрерывного режима работы лазера в рамках таких допущений, следует определить необходимое условие для возникновения непрерывной генерации, когда время жизни тх нижнего лазерного уровня является ограниченной величиной. Прежде чем это сделать, отметим, что стационарная населенность уровня 1 должна определяться условием баланса населенностей для фотонов, приходящих на уровень 1 и уходящих с него. Таким образом, при отсутствии генерации можно записать (М1/т1) = (А^/т21)> гДе Т21 — время жизни перехода 2 —» 1. Если теперь для простоты рассмотреть случай с двумя отдельными, равно вырожденными уровнями, то для возникновения генерации необходимо потребовать, чтобы ЛГ2 > А/'1. Согласно предыдущему выражению это означает, что
Т1 < т21- (7.3.1)
Если данное неравенство не выполняется, то работа лазера возможна в импульсном режиме лишь при условии, что длительность импульса накачки не превышает времени жизни верхнего уровня. Возникнув, лазерная генерация будет продолжаться до тех пор, пока число атомов, накопившихся на нижнем уровне (в результате вынужденного излучения), не станет достаточным для снятия инверсии населенностей. Поэтому такие лазеры называются лазерами на самоограниченных переходах. С другой стороны, если выражение (7.3.1) справедливо и величина постоянна и достаточно велика, то, в
конечном счете будет выполнено условие стационарной генерации. Теперь можно проанализировать это условие в предположении, что т2, так чтобы были применимы уравнения (7.2.16).
Рассмотрим вначале пороговое условие генерации лазера. Предположим, что в момент времени £ = 0 в резонаторе вследствие спонтанного испускания присутствует некоторое небольшое число фотонов ф* (например, ф^ = 1). При этом из уравнения (7.2.166) видно, что для выполнения неравенства (с? ф/сй) > О, должно выполняться условие (ВУаЫ) > 1/тс. Следовательно, генерация возникает в том случае, когда инверсия населенностей N достигнет критического значения Ис, определяемого выражением (см. также раздел 1.2):
Ые^(1/ЕУахс) = (у/Ы)9 (7.3.2),
При выводе которого использовались выражения (7.2.13) и (7.2.14). Соответствующее значение для критической скорости накачки Ир выводится из уравнения (7.2.16а), полагая (йЫ/дЛ) = 0, что соответствует устойчивому состоянию, а также полагая N = ЫС и ф = 0. Таким образом, можно видеть, что критическая скорость накачки соответствует ситуации, когда скорость 11ср накачки уравновешивает скорость Ыс/х спонтанного перехода с уровня 2, т. е.
Кср = К/х = (у/с/х), (7.3.3)
Где было использовано выражение (7.3.2).
Если Нр > то число фотонов ф будет возрастать от исходного значения, определяемого спонтанным излучением, и если Яр не зависит от времени, то число фотонов, в конечном счете, достигнет некоторого стационарного значения ф0. Это значение, а также соответствующее стационарное значение инверсии ЛГ0, выводятся из уравнения (7.2.16), если положить в них (йЫ/(И) = (й$/сИ) = 0. Таким образом, имеем:
ЛГ0-(1/В? л) = (у/аО, (7.3.4а)
Фо = Птс[Др-(ЛГ0/т)]. (7.3.46)
Следует отметить, что соотношение (7.3.46) было получено из выражений (7.3.4а), (7.2.14) и (7.2.15).
|
Рис. 7.3 Качественная зависимость инверсии населенностей N и полного числа фотонов ф в резонаторе от скорости накачки Яр |
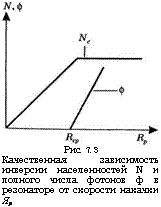 Выражения (7.3.4) описывают непрерывный режим работы четырехуровневого лазера. Рассмотрим их более детально. Сравнивая выражения (7.3.4а) и (7.3.2), можно видеть, что равенство ЛГ0 = ЛГС выполняется даже когда Щ > 11ср, т. е. инверсия в условиях стационарного состояния всегда равна критической или пороговой инверсии. Для лучшего понимания данного результата рассмотрим на рис. 7.3 график зависимости величин N и ф от скорости накачки Яр. Если К, р < то ф = 0 и инверсия N возрастает линейно с ростом При Ир = 11Ср все еще имеем N = ЛГС и ф = 0. Если теперь кр превышает то, как видно из выражения (7.3.4), инверсия населенностей И0
Выражения (7.3.4) описывают непрерывный режим работы четырехуровневого лазера. Рассмотрим их более детально. Сравнивая выражения (7.3.4а) и (7.3.2), можно видеть, что равенство ЛГ0 = ЛГС выполняется даже когда Щ > 11ср, т. е. инверсия в условиях стационарного состояния всегда равна критической или пороговой инверсии. Для лучшего понимания данного результата рассмотрим на рис. 7.3 график зависимости величин N и ф от скорости накачки Яр. Если К, р < то ф = 0 и инверсия N возрастает линейно с ростом При Ир = 11Ср все еще имеем N = ЛГС и ф = 0. Если теперь кр превышает то, как видно из выражения (7.3.4), инверсия населенностей И0
Остается постоянной и равна критической, тогда как ф0 линейно возрастает с ростом Нр. Иными словами, когда скорость накачки оказывается выше пороговой, в резонаторе лазера увеличивается число фотонов (т. е. электромагнитная энергия, запасенная в резонаторе); когда скорость накачки не превышает пороговую, растет только инверсия населенностей (т. е. энергия, запасенная в активной среде).
Теперь можно переписать выражение (7.3.46) в более простой форме, вынося член (Л^оЛ) = №с/т) = Вср за квадратные скобки. Таким образом:
Фо=(^о)—(ж-1), (7-3-5>
Т
Где
Х = НрШср (7.3.6)
Представляет собой относительное превышение скорости накачки. Нетрудно заметить, что как для оптической, так и для электрической накачки можно записать следующее:
Х = Рр/Ргн, (7.3.7)
Где Рр — мощность накачки, а Р1Н — ее пороговое значение. Подставляя выражения (7.3.7) и (7.3.4а) в уравнение (7.3.5) можно получить более удобную запись:
Л _ - А-ъУ тс
(7.3.8)
Где Аъ = (Уа/1) — поперечное сечение моды (область пучка), которое, как предполагается, должно быть меньше или равно поперечному сечению А = (V/I) активной среды.
|
 Запишем теперь выражение для выходной мощности. Используя выражения (7.2.18) и (7.3.8), получаем:
Запишем теперь выражение для выходной мощности. Используя выражения (7.2.18) и (7.3.8), получаем:
Pout =(-Aft-fs)[
(7.3.9)
Где Is = hv/<5T — интенсивность насыщения усиления для четырехуровневой системы [см. выражение (2.8.24)]. Это выражение согласуется с тем, которое получил Ригрод [5] в своем анализе «проход за проходом» для случая, когда зеркало 1 имеет стопроцентное отражение. Поскольку кривая зависимости Pout от Рр имеет вид прямой линии, пересекающей ось Рр в точке Pp = PthJ можно определить дифференциальный КПД лазера как
4s = dP0Ut/dPp, (7.3.10)
Где T|s — величина, которая оказывается постоянной для заданной лазерной схемы.
С помощью предыдущего выражения, а также уравнений, полученных в главе 6, можно получить весьма полезное и наглядное выражение для параметра т}8. Подставляя вначале Pout из формулы (7.3.9) в выражение (7.3.10), запишем:
Аъ hv у о 1
^ ~ стт ~2 ' Pth' (7.3.11)
Как для оптической, так и для электрической накачки подстановка выражения (6.2.6) или (6.4.26) в формулу (7.3.3) дает следующее соотношение:
|
|
(7.3.12)
Где, как уже оговаривалось, утр определяет разницу в частотах между верхним лазерным уровнем и основным состоянием; и А представляет собой площадь поперечного сечения активной среды. Из выражений (7.3.11)и(7.3.12) получаем:
|
|
(7.3.13)
Таким образом, можно записать:
(7.3.14)
Где: 1) г)р — эффективность накачки; 2) г)с = у2/2у — доля фотонов, сгенерированных на выходе резонатора (или, другими словами, эффективность связи на выходе резонатора). Здесь следует отметить, что в любом случае Лс< 1, причем единица достигается при уг = у* = 0; 3) цд = Ну/Нтр — доля минимальной энергии накачки, которая преобразуется в лазерную энергию (ее можно также обозначить как квантовую эффективность лазера); 4) =АЬ/А определяет часть площади поперечного сеченая активной среды, которая заполняется лазерным пучком (другими словами этот параметр можно назвать коэффициентом заполненця сечения активной среды или эффективностью сечения). Следует отметить, что в данном случае накачка считается однородной.
Пример 7.2. Непрерывный режим работы мощного А!<1:УАС лазера с оптической накачкой. Рассмотрим лазерную систему, изображенную на рис. 7.4. Стержень из ЫсЬУАО длиной 7,5 см и диаметром 6,35 мм (концентрация N(1 составляет 1% ) накачивается излучением криптоновой лампы высокого давления, помещенной вместе со стержнем в эллиптический осветитель. Резонатор лазера состоит из двух плоских зеркал, расположенных на расстоянии 50 см друг от друга. Коэффициент отражения первого зеркала составляет = 100%, а выходного зеркала И2 = 85%. Зависимость мощности Роиг на выходе зеркала 2 (в многомодовом режиме) от мощности электрической накачки Рр9 подводимой к криптоновой лампе, показана на рис. 7.5, [7]. Следует отметить, что речь идет о мощном непрерывном N(1:УАО лазере, выходная мощность которого превышает 200 Вт. Поскольку данный лазер генерирует на многих продольных и поперечных
|
|
#2=85%
|
1 |
![]()
|
2 |
![]() Рис. 7.4
Рис. 7.4
|
Ь = 50 см |
![]() Возможная схема резонатора непрерывного Кс1:УАО лазера с оптической накачкой
Возможная схема резонатора непрерывного Кс1:УАО лазера с оптической накачкой
Рис. 7.5
|
М О 2 4 6 8 ю Мощность лампы накачки Рр( кВт) |
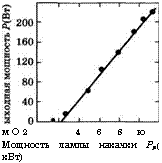
![]() Зависимость выходной мощности непрерывного излучения от входной
Зависимость выходной мощности непрерывного излучения от входной
Мощности лампы накачки
В мощном КсіїУАО лазере
(согласно работе Коэхнера [7])
Модах, то согласно рассуждениям, приведенным в разделе 7.2.1, было бы обосновано сравнить экспериментальные результаты с теоретическими расчетами, проводимыми в рамках рассмотренной пространственно-незави - симой модели скоростных уравнений. Действительно, в случае, когда входная мощность превышает пороговую, за исключением значений вблизи порога, экспериментальная кривая на рис. 7.5 демонстрирует линейную зависимость выходной мощности от входной, как это и следовало из выражения (7.3.9). Экстраполируя линейный участок данной кривой, можно определить пороговую мощность Рт = 2,2 кВт. Таким образом, после превышения накачки над порогом зависимость выходной мощности может быть представлена следующим приближенным выражением:
|
(7.3.15) |
![]() Рош = 53[(Рр/Р- 1].
Рош = 53[(Рр/Р- 1].
Где Рои( выражена в ваттах. Значение дифференциальной эффективности может быть легко найдено из выражения (7.3.15): = (<1Роиг/йРр) =
= 53/Р1Ъ = 2,4%. Сравним выражения (7.3.15) и (7.3.9), принимая во внимание (как уже обсуждалось в примере 2.10), что эффективное сечение перехода для длины волны X = 1,06 мкм (в материале КсЬУАО), а также время жизни верхнего уровня такого перехода составляют а = 2,8 • 1019 см2 и т = 230 мкс соответственно. Энергия фотона с такой длиной волны равна Нх = 3,973 • 10~19 х х (0,5/1,06) = 1,87 • 10~19 Дж, где значение 3,973 • 10-19 Дж есть энергия фотона с длиной волны 0,5 мкм (см. приложение 3). Далее находим значение насыщения интенсивности линии 18 = /гу/ат = 2,9 кВт/см2. Теперь можно принять Н2 = (1 “ а2 ~ Т2)« (1 — Т2), поскольку для зеркал с очень хорошим качеством напыления поглощение а2 может составлять менее 0,1%. Далее имеем у2 = -1п#2 = 0,162. Сравнивая выражения (7.3.15) и (7.3.9), получаем значение Аъ » 0,23 см2, которое можно сравнить с поперечным сечением стержня А «0,317 см2. Для того чтобы сравнить значения дифференциального КПД и пороговой мощности, полученные путем экстраполяции, с результатами теоретических расчетов, необходимо знать величину у, точнее у*. Поскольку ух = 0, выражение (7.3.12) с помощью (7.2.8) можно переписать в виде:
|
|
(7.3.16)
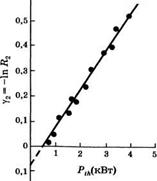
Следовательно, если провести несколько измерений пороговой мощности накачки при различных коэффициентах отражения #2, то должна получиться линейная зависимость величины у2 = —1п #2 от РгЛ. Именно такая
|
|
|
Рис. 7.6 Пороговая мощность накачки как функция коэффициента отражения зеркала (согласно работе Коэхнера [8]) |
Зависимость и наблюдается экспериментально, как это видно из рис. 7.6. Экстраполяция этого отрезка прямой на ось у2 дает, в соответствии с выражением (7.3.16), величину внутренних потерь (анализ Финдли и Клэя [9]). Таким образом, из рис. 7.6 получаем значение yf» 0,038 и, следовательно, полные потери у = (у2/2) + yt« 0,12.
Поскольку полные потери известны, можно, используя выражение
(7.3.14) , сравнить измеренное значение дифференциального КПД, r|s = 2,4%, с теоретическими результатами. Выбираем цс = у2/2у « 0,68. Также выбираем rq = АтрД = 0,89, где Хтр = 0,94 мкм — длина волны, соответствующая переходу с верхнего лазерного уровня в основное состояние для Nd: YAG лазера(см. рис. 2.15). Согласно предыдущим вычислениям, г)t = Ab/A » 0,72. Из выражения (7.3.14) получаем rjp = 5,5%, что вполне соответствует эффективности накачки для криптоновой лампы (см. также табл. 6.1). Рассчитываемое значение Pth может быть теперь легко получено из выражения (7.3.12), принимая во внимание, что hvmp & 2,11 • 10-19 Дж. Исходя из этого, получаем Pth «2,26 кВт, что достаточно хорошо согласуется с экспериментальными данными. Зная полные потери, можно также вычислить пороговую инверсию населенностей. Из выражения (7.3.2) находим Nc = 5,7 • 1016 ионов/см3. При доле примеси 1% общая концентрация атомов Nd составляет Nt = 1,38 • Ю20 ионов/см3. Таким образом, Nc/Nt = = 4,1 • 10~4, т. е. действительно инверсия населенностей составляет лишь очень небольшую долю полной населенности.
Пример 7.3. Непрерывный режим работы мощного С02 лазера. Рассмотрим лазерную систему, изображенную схематично на рис. 7.7, которая включает в себя неустойчивый резонатор положительной ветви, что обеспечивает большой объем моды и, следовательно, высокую выходную мощность. Длина резонатора составляет L= 175 см, а длина активной среды
I — 140 см. Активная среда состоит из газовой смеси C02:N2:He с соотношением парциального давления 1:1:8 и полным давлением 100 Topp. Для эффективного охлаждения газовая смесь прогоняется поперек оси резонатора. Как показано на рисунке, возбуждение газа осуществляется постоянным электрическим разрядом между двумя плоскими электродами (поперечный разряд, см. также рис. 6.196). На рис. 7.8 представлена типичная зависимость выходной мощности лазера Pout от входной мощности г* подводимой
Рис. 7.7
|
“і?!=13,5 м |
![]()
|
І? о=10 м — |
![]() Возможная схема резонатора мощного непрерывного С02 лазера
Возможная схема резонатора мощного непрерывного С02 лазера
|
-1=140 см -/=175 см |
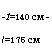
|
Р(кВт) |
![]()
|
S О О |
![]()
|
Ю |
![]() Рис. 7.8 Зависимость выходной мощности Р от мощности Рр, подводимой к электрическому разряду, для мощного непрерывного С02 лазера
Рис. 7.8 Зависимость выходной мощности Р от мощности Рр, подводимой к электрическому разряду, для мощного непрерывного С02 лазера
К электрическому разряду [10]. Экспериментальные точки на графике можно аппроксимировать выражением:
Pout = 6,66[(Pp/Pth) - 1], (7.3.17)
Где величина Pout дается в киловаттах, a Pth — пороговая мощность накачки, полученная путем экстраполяции (Pth « 44 кВт).
При давлении 100 Topp уширение линии генерации в С02 лазере обусловлено преимущественно столкновительными процессами. Полагая, что температура газа составляет Т = 400 К, получаем Avc « 430 МГц (см. пример 3.3), тогда как доплеровское уширение дает -50 МГц (см. пример 3.2). Для заданной длины резонатора разность частот между двумя соседними продольными модами составляет Av = c/2L = 107 МГц, и при значительном превышении накачки над порогом в резонаторе могут генерироваться несколько продольных мод. Кроме того, в генерации могут участвовать и несколько поперечных мод. Действительно, число Френеля (см. раздел 5.6.2) в данном случае оказывается достаточно большим (Neq = 7,4), и, как ожидается, потери нескольких поперечных мод сравнимы по величине (см. рис. 5.21). Следовательно, поперечный профиль пучка внутри резонатора можно считать достаточно однородным. Таким образом, имеет место случай, когда описанная ранее модель скоростных уравнений дает достаточно хорошее приближение; и поскольку С02 лазер работает по четырехуровневой схеме, можно сравнить выражения (7.3.17) и (7.3.9). Для этого необходимо знать пропускание Т2 выходного зеркала. Поскольку поперечный профиль пучка считается достаточно однородным, будем использовать приближение геометрической оптики. Значение Т2, которое соответствует потерям за полный (двукратный) проход в неустойчивом резонаторе, определяется выражением Т2 = (М2 - 1 )/М2 = 0,45 (см. выражение (5.6.5)). Здесь величина М представляет собой увеличение за полный проход резонатора и задается выражением М = RX/R^ = 1,35, где Rx и R2 — радиусы кривизны соответствующих зеркал (R2 < 0, т. к. зеркало 2 является вогнутым). Срав
нивая выражения (7.3.17) и (7.3.9) и используя соотношениеу2 = - In (1 - Т2) » « 0,6, получаем AbIs = 22,3 кВт. Диаметр пучка в резонаторе (см. также рис. 5.18б) составляет D = 2Ма2 « 7,6 см, где 2а2 = 5,7 см — диаметр выходного зеркала (см. рис. 7.7). Таким образом, получаем Ab = nD2/4 » 45 см2 и 18» 500 Вт/см2. Данное значение хорошо согласуется с теоретическими оценками интенсивности насыщения линии для С02 лазера такого типа [11].
Используя данные, приведенные на рис. 7.8, вычислим теперь коэффициент усиления g активной среды до момента насыщения (т. е. когда лазерная генерация еще не началась) при входной мощности накачки Р « 140 кВт. Действительно, имеем:
G = N2a = E*-Nna = E*-l, (7.3.18)
*th rth 1
Где N2 — населенность верхнего уровня до момента насыщения при Рр = = 140 кВт, a N2o — населенность этого уровня при Р Следует отметить,
Что выражение (7.3.4а) использовалось для iV20, так что коэффициент усиления насыщения g0 = N20g имеет вид g0 = у/I. Для того чтобы рассчитать g0t необходимо знать потери резонатора у за один проход. Предположим, что потери на зеркале за счет поглощения и рассеяния составляют 2%. На самом деле, для мощной лазерной генерации на длине волны 10,6 мкм полированные и охлаждаемые водой зеркала, изготовленные из меди, обеспечивают существенно более высокие потери, чем многослойные диэлектрические зеркала. Далее, имеем yt» 0,02, и поскольку ух = 0, у2 = 0,6, получаем у «0,32. Подстановка этого значение в выражение (7.3.18) дает значение g0 = 6,3 • 10~3 см-1. Коэффициент усиления до момента насыщения может быть легко получен экспериментально путем измерения коэффициента усиления активной среды при снятых зеркалах резонатора. Измеренные значения коэффициента усиления для такого типа лазерной системы достаточно хорошо согласуется с теоретическими оценками, полученными здесь [12].
Сравним теперь экспериментальное значение дифференциального КПД, полученного из рис. 7.8, с расчетными оценками. Положим г|р « 0,8 (см. рис. 6.28), т)с = у2/2у = 0,94, rt« 1 и r|g = hv/hvmp = 0,4 (см. схему энергетических уровней С02 лазера, глава 10). Из выражения (7.3.14) получаем = 0,3, что значительно превышает значение, полученное экспериментально из рис. 7.8 (rjs« 0,21). Это расхождение можно объяснить как минимум двумя различными обстоятельствами:
1. Коэффициент заполнения r|f может быть заметно меньше единицы. Возможно, если бы в данной задаче значение было взято из предыдущего примера, rj, = 0,73, то теоретический результат практически бы полностью совпал с экспериментальными данными.
2. Данные на рис. 7.7 относятся к системе, работающей частично по замкнутому циклу, и в этом случае продукты электрического разряда (большей частью СО и 02) имеют склонность накапливаться в газовой смеси и уменьшать тем самым КПД накачки ниже теоретического значения 80%. В действительности для большинства используемых С02 лазеров крайне редко достигается значение дифференциального КПД больше, чем ~20%.
Рассмотренный пример позволяет наглядно понять механизм уменьшения дифференциального КПД от его предельного теоретического значения, ограниченного сверху квантовой эффективностью или квантовым выходом (г|9 = 40%).