ПРИНЦИПЫ ЛАЗЕРОВ

ПРОСТРАНСТВЕННАЯ И ВРЕМЕННАЯ КОГЕРЕНТНОСТЬ ОДНОМОДОВЫХ И МНОГОМОДОВЫХ ЛАЗЕРОВ

Рассмотрим сначала непрерывный лазер, генерирующий на одной попе­речной и продольной моде. Чуть выше порога генерации (как уже было пока­зано в разделах 7.10 и 7.11) флуктуациями амплитуды в первом порядке приближения можно пренебречь. Тогда аналитические сигналы волны в двух точках гх и г2 можно записать следующим образом:

Е(г1У 0 = а01г(г1)ехр {Дсо£ - ф(*)]}> (11.3.31а)

Е(г2, 0 = а0и(г2)ехр{Дсо* - ф(*)]}» (11.3.316)

Где а0 — константа, и(г) — функция, описывающая амплитуду моды и со — угловая частота в центре полосы генерации. Подстановка выражений (11.3.31) в (11.3.6) дает у(1) = ^(г1)1г*(г2)/|гг(г1)||^(г2)|, откуда следует, что |у(1)| = 1. Та­ким образом, одномодовый лазерный пучок обладает полной пространствен­ной когерентностью. С другой стороны, временная когерентность определя­ется шириной полосы генерации Ачь. Например, ширина полосы генерации в одномодовом монолитном кольцевом Ы(1:УАО лазере (см. рис. 7.26) состав­ляет ь = 20 кГц, и следовательно, время когерентности тсо = 1 /Аь ^ 0,05 мс. В этом случае длина когерентности составит Ьс = стС0 =15 км (очень боль­шое значение).

Рассмотрим теперь лазер, генерирующий на одной поперечной и на мно­гих продольных модах (I продольных мод). Аналитические сигналы (или поля) в двух точках гг и г2, принадлежащих одному и тому же волновому фронту, в общем случае можно представить через амплитуды мод резонатора следующим образом:

£01.0 = X * а*и(г1)е*р{ Л®** - Фа (£)]}, (11.3.32а)

1

£(Пг»0 = Х*а*ы(г2)ехр{Л<М-<Ы*)]}> (11.3.326)

1

Где ак — постоянные множители, ашйифА — соответственно частота и фаза 1г-й моды. Следует заметить, что поскольку поперечное распределение поля у всех мод одинаковое (например, распределение моды ТЕМ00), амплиту­да и моды не зависит от модового индекса 1г. Таким образом, функция и(г) может быть вынесена за знак суммы в обоих выражениях (11.3.32). Таким образом, получаем:

Е(г2, г) = [и(г2)/ы(г1)]£(г1, 0- (11.3.33)

Это означает, что всякий раз, когда изменение величины Е(гх, £) во вре­мени наблюдается в точке гх, то с точностью до коэффициента пропорцио­нальности такое временное изменение будет наблюдаться в точке г2. Подста­новка соотношения (11.3.33) в выражение (11.3.6) дает |у[72]| = 1. Таким обра­зом, лазерный пучок, состоящий из многих продольных мод с одинаковым поперечным распределением (например, как в моде ТЕМ00), по-прежнему обладает полной пространственной когерентностью. Временная когерент­ность, если фазы всех мод случайны, снова равна обратному значению шири­ны полосы генерации. При отсутствии в резонаторе частотно-селектирую - щих элементов ширина полосы генерации может быть теперь сравнима с шириной линии усиления и, следовательно, время когерентности может быть много меньше, чем в предыдущем примере (от наносекунд до пикосекунд). Однако в случае синхронизации мод временная когерентность может стать очень большой, так что лазер с синхронизацией мод может в принципе обла­дать полной пространственной и временной когерентностью.

В качестве последнего случая было бы необходимо рассмотреть лазерную генерацию на многих поперечных модах. Как будет показано в следующем примере, такой лазер обладает только частичной пространственной когерент­ностью.

Х*а*а*М>К(г2)

1______________

1/2

Х*|а*Р1«*(г1)12

1

Если теперь обозначить через комплексный вектор, описываемый компонентами акик(гх) в /-мерном пространстве, и аналогично ввести обо­значение для величины Н2, то можно записать их скалярное произведение в виде: г

-К2 = ^кака1ик{г1)ик(г2). (11 3 39)

С другой стороны, амплитуду этих двух векторов можно записать как

1/2

X* |а*12к*(г1)|2

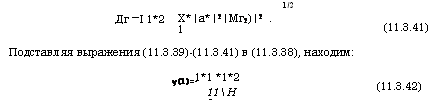Из неравенства Шварца следует, что поскольку * аН2, где а — кон­станта, всегда будет иметь место неравенство [у*1*! < 1.

TOC o "1-5" h z Рис. 11.5 _,

Степень пространственной ь

Когерентности ^■—

В плоскости, находящейся -'

на расстоянии г от независимых излучателей, расположенных в области диаметром й

Что касается пространственной когерентности, здесь следует отметить следующее: поскольку электромагнитная волна спонтанно испускается мно­гими независимыми излучателями, она является полностью некогерентной, если рассматривать ее в некоторой близости к источнику света. Между тем, степень пространственной когерентности может увеличиваться при доста­точном удалении области наблюдения от источника. Данная ситуация мо­жет быть объяснена с помощью рис. 11.5, где изображены некоррелирован­ные излучатели (обозначены точками), расположенные внутри некоторой апертуры отверстия диаметром <2, которое проделано в экране 5. Излучение в этом случае будет распространяться в пределах телесного угла 4л. Предста­вим, что пространственная когерентность между точками и Р2 измеряет­

Ся на некотором расстоянии г от излучателей. Для простоты, пусть точка Рг расположена на оси симметрии системы, и пусть г — расстояние между дву­мя указанными точками. Из рисунка видно, что при очень малых значе­ниях г точки Рх и Р2 располагаются непосредственно напротив определенно­го излучателя (допустим, что расстояние между точками: г < <2/2), и поля в этих точках будут полностью некоррелированы. Однако при увеличении рас­стояния г каждая из этих двух точек будет принимать все больший и боль­ший вклад от других излучателей и, таким образом, поля в этих точках бу­дут все больше и больше скоррелированы. Вычисление степени пространст­венной когерентности |у(1)| как функции координаты гиг выходит за рамки тематики данной книги, и более подробно ознакомиться с данным вопросом можно в работе [3]. Здесь лишь можно обратить внимание на то, что |у(1)| яв­ляется функцией безразмерной величины (п2/Хг) и, в качестве примера, мож­но показать, что |у(1)| = 0,88 при

Г = 0,16(А,;г/<2). (11.3.43)

Этот результат будет использован в следующем разделе.