ПРИНЦИПЫ ЛАЗЕРОВ

ПРИНЦИП РАБОТЫ ЛАЗЕРА

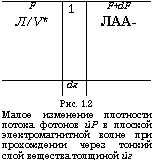Рассмотрим два произвольных энергетических состояния 1 и 2 некоторого вещества и обозначим соответственно через Nx и N2 их населенности. Если в данном веществе вдоль оси г распространяется плоская электромагнитная вол­на с плотностью потока фотонов F (рис. 1.2), то ма­лое изменение плотности потока dF в тонком слое толщиной dz (заштрихованная область на рис. 1.2) будет обусловлено как процессами вынужденного излучения, так и поглощения. Пусть через S обо­значена площадь поперечного сечения пучка. Раз­ность между числами фотонов, покидающих вы­деленный объем и поступающих в него в единицу времени, будет при этом равна SdF. Поскольку в каждом акте вынужденного излучения рождает­ся, а в каждом акте поглощения уничтожается один фотон, то величина SdF должна равняться раз­нице между числом актов вынужденного излучения
и поглощения, произошедших в рассматриваемом объеме в единицу време­ни. Используя соотношения (1.1.4) и (1.1.6), можно записать: SdF = (VpN2 -

- W12N1)(Sdz), где Бйг — объем заштрихованной области. Отметим, что при выводе этого соотношения не учитывались спонтанные излучательные и бе - зызлучательные переходы, поскольку последние не приводят к рождению новых фотонов, а спонтанно испущенные фотоны не дают вклада в падаю­щую плоскую волну. Действительно, спонтанное излучение испускается по всем направлениям и на длине волны, не обязательно совпадающей с длиной волны падающего излучения.

Здесь и ниже будем полагать, для простоты, что рассматриваемые со­стояния либо невырождены, либо имеют одинаковую кратность вырожде­ния (т. е. = ё2). Из приведенного выше соотношения с помощью (1.1.5) и

(1.1.7) получаем

(1Р = а*1ЛГ2 - N^2. (1.2.1)

Здесь введено обозначение а21 = <*12 = ст, а параметр а будет далее называться поперечным сечением перехода.

Из соотношения (1.2.1) следует, что в случае Ы2 > среда ведет себя как

Усиливающая (т. е. йР/йг > 0), а в случае ЛГ2 < — как поглощающая. Из­

Вестно, что при тепловом равновесии населенности состояний описываются статистикой Больцмана. Так, если Щ и А^| — равновесные населенности двух состояний, то

Е2 — Ех

No

—- = ехр-

(1.2.2)

Где k — постоянная Больцмана, а Т — абсолютная температура среды. Та­ким образом, видно, что в случае теплового равновесия iVf <N{. Согласно

(1.2.1) среда при этом должна поглощать излучение на частоте v0. Именно это и происходит при обычных условиях. Однако если каким-то образом реа­лизуются неравновесные условия, при которых N2 > Nl9 то среда будет вести себя как усилитель. В этих случаях говорят, что в среде существует инверсия населенностей. Имеется в виду, что разность населенностей N2 - Nx проти­воположна по знаку той, которая существует при тепловом равновесии (Щ - Щ < 0). Среду, в которой создается инверсия населенностей, называют активной средой.

Если частота перехода v0 = (Е2 - Ex)/h попадает в СВЧ-диапазон, то уси­литель такого типа называют мазерным (англ. maser), что является акрони­мом английского названия соответствующего процесса: Microwave Amplifi­cation by Stimulated Emission of Radiation — усиление микроволн за счет вынужденного испускания излучения. Если же частота перехода находится в оптическом диапазоне, то усилитель называют лазерным. Соответствую­щий акроним (англ. laser) получен из предыдущего заменой слова Micro­wave в названии на Light (свет).

Для того чтобы усилитель превратить в генератор, необходимо допол­нить его подходящей положительной обратной связью. В СВЧ-диапазоне это достигается тем, что активную среду помещают в объемный резонатор, имею-

Выходной

Пучок

Зеркало! Активная среда Зеркало 2

Щий резонанс на частоте у0. В случае лазерного генератора положительную обратную связь обычно обеспечивают путем размещения активной среды ме­жду двумя зеркалами с высоким коэффициентом отражения (например, ме­жду плоскопараллельными зеркалами, как показано на рис. 1.3). При этом плоская электромагнитная волна, распространяющаяся в среде вдоль направ­ления нормали к плоскостям зеркал, будет поочередно отражаться от них обратно и усиливаться при каждом проходе череадктивную среду. Если одно их двух зеркал (например, зеркало 2) сделано частично прозрачным, то за этим зеркалом можно получить пучок выходящего из генератора излучения.

Важно понимать, что для работы как мазерных, так и лазерных генера­торов требуется выполнение определенного, так называемого порогового, условия. Так, лазерный генератор начинает излучать тогда, когда усиление в активной среде компенсирует потери в нем (например, потери за счет час­тичного выхода излучения из резонатора через зеркало). Согласно соотно­шению (1.2.1) усиление за один проход в активной среде (т. е. отношение плотностей потока фотонов на выходе и на входе) составляет ехр{а[^У2 - N хЮ» где I — длина активной среды. Обозначим теперь энергетические коэффици­енты отражения зеркал (рис. 1.3) соответственно через ий2, а внутрен­ние потери за один проход внутри резонатора лазера — через Ц. Если 2? — это плотность потока фотонов в резонаторе, отраженных в данный момент времени от зеркала 1 и движущихся в направлении зеркала 2, то плотность потока фотонов 2^', отраженных от зеркала 1 после одного полного прохода резонатора, будет составлять

Г = Рехр{ст(АГ2 - Ыг)1} х (1 - Ц)Я2 х ехр{а(#2 - N^1} х (1 - Ц)^.

На пороге генерации должно выполняться условие 2^ = 2'1' и, следовательно, соотношение 2?!2?2( 1 - Х^2ехр{2а(А^2 - Ыг)1} = 1. Из него следует, что порог ге­нерации достигается тогда, когда инверсия населенностей N = (ЛГ2 - N1) воз­растает до величины, называемой критической, или пороговой, инверсией населенностей у и равной

N. = -[1п + 21п(1 - Ц)У2Ы. (1.2.3)

Соотношение (1.2.3) можно упростить, вводя обозначения

У2 = Чп#! = -1п(1 - 7), (1.2.4а)

У2 = -1п Л2 = -1п(1 - Т2), (1.2.46)

У-ЧпЦ-Х,*), (1.2.4В)

Где ТгиТ2 — энергетические коэффициенты пропускания зеркал (для упро­щения поглощением в зеркалах пренебрегается). Подстановка соотношений

(1.2.4) в (1.2.3) дает

ЛГс = у/Ы, (1.2.5)

У = [2ъ+(у1 + у2)]/2.

Заметим, что величину у19 определенную соотношением (1.2.4в), можно на­звать внутренними логарифмическими потерями. Действительно, если!^ <С 1, что обычно выполняется, то у 1 = Аналогично, поскольку как 7, так и Т2 характеризуют потери за счет выхода излучения из резонатора, то величины У! иу2, определяемые соотношениями (1.2.4а-б), можно назвать (логариф­мическими ) потерями на зеркалах резонатора. Таким образом, величину 2у* + (ух + Уг)> стоящую в числителе выражения (1.2.3), будем называть (лога­рифмическими) потерями за один полный обход резонатора, а вдвое мень­шую величину у из сотношения (1.2.6) — (логарифмическими) потерями за один проход резонатора.

При достижении пороговой инверсии населенностей из спонтанного излу­чения развивается генерация. Действительно, фотоны, спонтанно испущен­ные вдоль оси резонатора, инициируют процесс усиления излучения. Этот ме­ханизм и лежит в основе работы лазерного генератора, который обычно назы­вают просто лазером. Заметим, что, согласно смыслу акронима «лазер», его следует применять только по отношению к генераторам видимого излучения. Однако то же самое название широко используется для обозначения любого устройства, испускающего вынужденное излучение, — будь то в дальнем или ближнем ИК-, УФ - или даже в рентгеновском диапазонах. Чтобы уточнить тип испускаемого лазером излучения, говорят, соответственно, о лазерах ин­фракрасного, видимого, ультрафиолетового или рентгеновского диапазонов.