ПРЕОБРАЗОВАНИЕ ШИРИНЫ ПОЛОСЫ И ЧАСТОТНАЯ МЕТРОЛОГИЯ С ПОМОЩЬЮ ФЕМТОСЕКУНДНЫХ ЛАЗЕРНЫХ ИМПУЛЬСОВ
Гребенка весьма прецизионно определенных и эквидистантно расположенных линий была бы крайне полезной для частотной метрологии.[79] Действительно, такая гребенка позволяет непосредственно связать друг с другом две отдельные оптические частоты и сопоставить их с высоко прецизионной опорной частотой, соответствующей частоте сверхтонкого расщепления основного уровня атома цезия.[80] Иными словами, такая гребенка могла бы быть линейкой с прецизионными делениями [33, 34].
На первый взгляд, можно подумать, что спектр излучения лазера, генерирующего на многих продольных модах, годится для этой цели. Однако этот спектр не является гребенкой прецизионно эквидистантных линий. В самом деле, разность между двумя соседними модами можно записать как
Ау = с/2Ье, где Ье = Ье(п) с зависимостью от п — показателя преломления материала (материалов) внутри резонатора лазера. Таким образом, из-за дисперсии материала имеем п = п(у), и, соответственно, Ау = Ау(у), т. е. резонатор обладает дисперсионными свойствами. Поэтому, чтобы получить гребенку точно эквидистантно расположенных линий, необходимо использовать особые методы, которые, вообще, относятся к категории преобразования ширины полосы.
Как было показано в разделе 8.6, существует особый режим лазера, называемый непрерывной генерацией с синхронизацией мод, в результате которой генерируется непрерывная последовательность ультракоротких лазерных импульсов. Частота повторения импульсов в этой последовательности обратно пропорциональна времени обхода светом длины резонатора, т. е. уг = 1/гг, где:
В этом выражении 1Ь — длины, а 1)Ьё — соответствующие им групповые скорости в материалах, находящихся в резонаторе. Фурье-спектр такой последовательности представляет собой эквидистантные линии, разделенные интервалом уг, и при точно стабилизированном резонаторе получается вполне определенная гребенка частот. Таким образом, лазер с синхронизацией мод является не только источником ультракоротких импульсов, но и источником гребенки эквидистантных оптических частот. Однако окончательная трудность точного определения этой гребенки обусловлена тем, что для любого материала, в том числе и для находящегося внутри резонатора лазера, групповая скорость, строго говоря, отличается от фазовой (см. разд. 8.6.4.1). Из-за этого огибающая волны излучения А(і) для каждого ультракороткого импульса движется с групповой скоростью иё, в то время как несущая волны движется с фазовой скоростью ирк. В результате после каждого обхода резонатора несущая частота сдвигается по отношению к огибающей, т. е. по
|
|
|
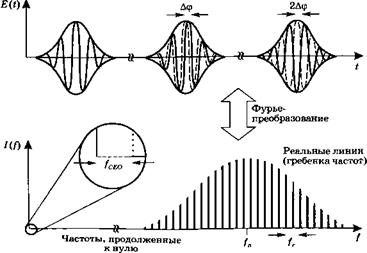
Рис. 12.16 Последовательность фемтосекундных импульсов (несколько периодов), испускаемых титан - сапфировым лазером с керровской линзой, и соответствующий спектр |
Отношению к импульсу, на фазовый угол Аф (см. рис. 12.16), который дается выражением:
Д<р = 2соУГ—-- О, (12.6.2)
Где viph — фазовые скорости в материалах внутри резонатора. Отметим, что поскольку изменение Аф на величину кратную 2п не изменяет электрическое поле волны импульса, реальное значение имеет величина угла
А(Рсео = Афто(12п. (12.6.3)
Этот угол обозначается как сдвиг несущая-огибающая (СЕО).
С помощью Фурье-преобразования можно показать, что спектр гребенки состоит из ряда эквидистантных линий частот, которые определяются как
= ^ уСЕОу (12.6.4)
Где п — целое число, а 2пусео = 2^СЕО = А<рСЕО/гн = АфС£0уг. Из этого также следует, что если мы продвинем спектр к нулевой частоте, т. е. для п = 0, то линии будут сдвинуты от нуля на частотный интервал VСео = /обо = АфсяоЛг* (см. врезку на рис. 12.16). Из (12.6.4) следует, что если уг и уСЕО стабилизированы и измерены по отношению к цезиевому стандарту частоты, то возможно определить точное значение частоты в гребенке, зная величину п.
Измерение частоты уг не составляет труда (обычно она лежит в области от десятков МГц до нескольких ГГц), и ее можно стабилизировать путем контроля длины резонатора. Ситуация с усео более сложная, поскольку, как говорилось выше, она зависит от разности между групповыми скоростями V# и фазовыми скоростями в резонаторе лазера. Это означает, что регулировка и контроль уС£0 возможны путем изменения величины дисперсии внутри резонатора (см. разд. 8.6.4.3). Но для прецизионной стабилизации частоты необходимо знать ее точное значение. Это можно осуществить, используя методику так называемого «/-2/» гетеродинирования, схема которой показана на рис. 12.17. Принцип действия можно пояснить, если мы предположим, что спектр гребенки простирается на октаву, т. е. если на высокочастотном краю гребенки существует частота у*, а на низкочастотном краю —
|
Ик Излучение |
|
Дихроическое зеркало, пропускающее f и отражающее f. Видимое? -О—(НЧ:------------- ^----- |
|
Микрострукту- Рированное Волокно |
|
Фемтосекундный Лазер |
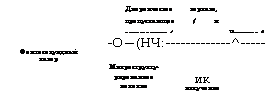 |
|
|
|
|
Fr Контроль |
![]() Генератор второй Фильтр Фотоэлектрический гармоники приемник
Генератор второй Фильтр Фотоэлектрический гармоники приемник
Рис. 12.17
Схема для измерения, контроля и стабилизации частоты усео («/-2/4 гетеродинирование)
Частота, такие, что т = 2п. В значениях vr и vCЈ0 эти частоты можно соответственно выразить как v* = mvr + СЕО = 2nvr + vCEO и v1 = nvr + CEO.
Пусть теперь пучок на частоте vln преобразуется во вторую гармонику, тогда мы получаем пучок на частоте 2nvr + 2vceo. Если теперь этот пучок второй гармоники и пучок на частоте посылаются на фотоэлектрический приемник, то на выходе его получится разностная частота, даваемая как 2vln - V* =vCEo• Таким образом, с помощью радиочастотного спектроанализатора можно будет измерить точное значение vCE0. Затем этот сигнал можно использовать с помощью подходящей электронной схемы, осуществляющей обратную связь, для контроля дисперсии внутри резонатора, стабилизируя тем самым генератор гребенки частот, получаемых за счет синхронизации мод.
На практике лазером с синхронизацией мод, используемым для этой цели, чаще всего является фемтосекундный титан-сапфировый лазер с керровской линзой (KLM Ti:sapphire laser), см. разд. 8.6.3.2, поскольку ширина полосы усиления титан-сапфира достаточно велика (более 100 ТГц, см. табл. 2.2). Для обеспечения нужного значения дисперсии в резонаторе используется система пар призм (см. разд. 8.6.4.3). В данном случае используются лишь две призмы, например призмы I и И, как показано на рис. 8.26, при расположении плоскости ММ' зеркала резонатора. Тонкие перемещение и наклон этого зеркала позволяют контролировать как длину резонатора, так и дисперсию внутри его. Однако следует, что ширина полосы в 100 ТГц синхронизованных мод недостаточна, чтобы иметь ширину спектра титан-сапфирово - го лазера, простирающегося более, чем на октаву. Поэтому пучок лазера на титан-сапфире с синхронизацией мод запускается в специальное микрострук - турированное оптическое волокно (которое также называют волокном типа фотонного кристалла — PCF), в котором спектр значительно уширяется за счет эффекта фазовой самомодуляции. В этом волокне кварцевая сердцевина очень малого диаметра (-1,5 мкм) окружена кольцом полых трубочек. Уникальные свойства дисперсии такого волокна таковы, что ноль дисперсии групповых скоростей в волокне сдвигается в область спектра титан-сапфиро - вого лазера. Это позволяет использовать достаточно длинное волокно и, соответственно, получать нужное уширение спектра. В результате генерируется гребенка частот, спектр которой простирается более, чем на октаву. Итак, использование фемтосекундного титан-сапфирового лазера вместе с микро - структурированным волокном при прецизионном контроле частоты vr путем стабилизации длины резонатора и vCEO с помощью методики «f-2f* открыло исключительно важную возможность прецизионного измерения оптических частот. Этот революционный подход сильно упрощает измерения оптических частот и предоставляет возможности для создания беспрецедентно точных полностью оптических атомных часов. Как известно, любые точные часы включают в себя колебательное устройство (генератор), которое создает «тиканье» во времени, и счетчика, показывающего число этих циклов. Например, в цезиевых часах такими колебаниями является прецессия электрона вокруг спина ядра. Если мы рассмотрим историю измерения времени и сравним такие часы, как солнечные, маятниковые и кварцевые, то увидим, что
Они становились все более точными по мере увеличения частоты колебаний. Это обусловлено тем, что большая частота делит время на меньшие интервалы. В оптических часах «тиканье» происходит на частоте в сотни ТГц, и они являются источником регулярных фемтосекундных «щелчков».
Сверхточные оптические часы будут полезны в целом ряде применений. Они также будут способствовать новым открытиям в фундаментальной науке. Один пример — исследование мировых констант, которые могут оказаться изменяемыми в пространстве или испытывать медленный дрейф во времени по мере эволюции нашей Вселенной. Другой пример — использование их в качестве опорного сигнала в радиотелескопах с большой базой. Наконец, технические применения, такие как спутниковая навигация и системы телекоммуникаций, также могут быть значительно улучшены с помощью этой технологии.