ПРИНЦИПЫ ЛАЗЕРОВ

ПРЕОБРАЗОВАНИЕ АМПЛИТУДЫ: ЛАЗЕРНОЕ УСИЛЕНИЕ

В данном разделе рассмотрим работу лазерного усилителя, используя модель скоростных уравнений [6-8]. Допустим, что плоская волна постоян­ной интенсивности I падает (в точке 2 = 0) вдоль направления г на лазерный усилитель длиной I. Ограничимся рассмотрением случая, когда падающее излучение имеет вид импульса (импульсное усиление). Случай усиления не­прерывного пучка (стационарное усиление) описывается в работе [8].

Вначале рассмотрим случай, когда усиливающая среда работает по четы­рехуровневой схеме, и предположим, что длительность входного импуль­са тр лежит в диапазоне <С тр т, где и т — время жизни нижнего и верх­него уровней активной среды усилителя соответственно. В этом случае насе­ленность нижнего уровня в усилителе можно положить равной нулю. Это является, по-видимому, наиболее подходящим набором условий для рассмот­рения механизма лазерного усиления, например в случаях, когда нужно уси­лить импульс излучения Nd: YAG лазера, работающего в режиме модуляции добротности. Также предположим, что накачкой и релаксацией населенно­сти верхнего уровня во время действия импульса можно пренебречь и что переход является однородно уширенным. Используя эти допущения, с помо­щью выражения (2.4.17) (в котором полагается F = I/hv) запишем скорость изменения инверсии населенностей N(t, z) в точке z внутри усилителя в сле­дующем виде:

Ж = _ЖАГ = _Ж, (12.3.1)

Dt Г8

Где

Г8 = (дv/g) (12.3.2)

— плотность энергии насыщения усилителя (см. выражения (2.8.29)). Сле­дует заметить, что в уравнении (12.3.1) имеет место частная производная, поскольку величина N должна быть функцией двух аргументов — ги^,т. е. N = N(t, г), вследствие того, что I = I(t, z). Отметим также, что решением уравнения (12.3.1) может быть функция N(t):

N(t) = N 0ехр {—(Г/Г s)}, (12.3.3)

Где N0 = N(—i) — населенность верхнего уровня усилителя до момента появ­ления лазерного импульса, которая определяется как накачкой, так и спон­танной релаксацией, и где величина

Г(г)= 1(г, П<Н (12.3.4)

—оо

Представляет собой полную плотность энергии лазерного излучения.

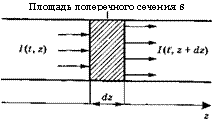
Теперь получим дифференциальное уравнение, описывающее временное и пространственное изменение интенсивности I. Для этого вначале запишем уравнение для скорости изменения плотности р электромагнитной энергии в единичном объеме активной среды длиной <1г с поперечным сечением 5 (за - штрихованная область на рис. 12.1):

= +(Ёр

01-и, лЧат№!’ (12-3-5>

Где член (др/д£)! соответствует вынужденному излучению и поглощению в усилителе, (др/д£)2 — потерям в усилителе (например, потерям вследствие рассеяния), (др/д£)3 — полному потоку фотонов через объем среды. С помо­щью выражения (2.4.17), полагая в нем ^ = 1/Лу, получаем:

= VNhv = оЫ1. (12.3.6)

Также из соотношений (2.4.17) и (2.4.32) следует, что:

= -1¥аМаНи = - а/, (12.3.7)

2

Где Ыа — плотность соответствующих центров потерь, ¥а — вероятность по­глощения и а — коэффициент поглощения в этих центрах. Для вычисления (Эр/Э£)3 снова обратимся к рис. 12.1, при этом величина (др/д^Бйг представ­ляет собой скорость изменения энергии фотонов в элементарном объеме, обу­словленная разностью между входной и выходной мощностью лазера. Те­перь, записывая (Эрг) -1(£, г 4- йг)], получаем:

ЭрЛ. 81 ,

С помощью выражений (12.3.6)-(12.3.8), полагая, что (др/д£) = (д!/сд£), уравнение (12.3.5) можно записать в виде:

-~+~ = суШ-а1, (12.3.9)

С О* 02

Рис. 12.1

К вычислению скорости изменения энергии фотонов в элементарном объеме лазерного усилителя с длиной <1г и с площадью сечения 5»

Оно вместе с уравнением (12.3.1) полностью описывает процесс усиления. Следует заметить, что это уравнение имеет обычный вид нестационарного уравнения переноса.

Уравнения (12.3.1) и (12.3.9) должны теперь решаться с соответствую­щими граничными и начальными условиями. За начальное условие берется N(0, г) = Ы0, где ЛГ0 — населенность верхнего уровня усилителя до момента появления лазерного импульса. Очевидно, что граничное условие задается интенсивностью /0(*) светового импульса, который поступает в усилитель, т. е. /(£, 0) = /0(0* При незначительных потерях в усилителе (т. е. в случае пренебрежения членом -а/) решение уравнений (12.3.1) и (12.3.9) можно записать в виде:

/(г, т) = /0(тШ-[1-ехр (~gz)]exр

Где x = t - (z/c), a g = gN0 — коэффициент ненасыщенного усиления усилителя.

Из уравнений (12.3.1) и (12.3.9) можно также вывести дифференциаль­ное уравнение для полной плотности энергии Г(2) импульса, заданной выра­жением (12.3.4). Таким образом, интегрируя обе части уравнения (12.3.1) по времени (в интервале от t = - со до t = +оо) и используя соотношение (12.3.3), получаем:

( AT/d*/rs) = N0 - АГ(+оо) = N0[ 1 - exp (-Г/Г8)].

Далее, интегрируя обе части уравнения (12.3.9) по времени (в том же временном интервале), а также используя выражение для [ Г°° JSfldt/TA и запись /(+оо, z) = /(-оо, z) = 0, получаем: ' '

= ^Г8[1-ехр (-Г/Г8)]-аГ.

Отсюда, снова пренебрегая потерями в усилителе, находим:

(12.3.12)

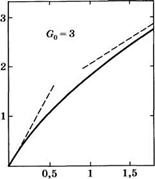
Где G0 = exp (gl) — ненасыщенное усиление усилителя (т. е. до момента насы­щения) и Tin — плотность энергии входного пучка. В качестве характерного примера на рис. 12.2 представлена кривая зависимости отношения Г/Гs от Tin/Ts при G0 = 3. Заметим, что в случае Tin <С Г8 выражение (12.3.12) можно приближенно записать в виде:

Г(0 = <2оГш,

Т. е. нетрудно видеть, что выходная плотность энергии растет линеино с вход­ной плотностью (режим линейного усиления). Также на рис. 12.2 построена зависимость, описываемая выражением (12.3.13), в виде штриховой пря­мой, выходящей из начала координат. Однако из рисунка видно, что при больших входных плотностях энергии величина Г увеличивается с ростом Т1п

С более низкой скоростью, чем предсказывает выражение (12.3.13), т. е. про­исходит насыщение усилителя. При Гin Гs (режим глубокого насыщения) зависимость, описываемая выражением (12.3.12), может быть аппроксими­рована следующим образом:

T(l) = rin + girs. (12.3.14)

На рис. 12.2 также изображена вторая штриховая прямая, вычисленная по формуле (12.3.14). Следует заметить, что при больших входных плотно­стях энергии выходная плотность энергии линейно зависит от длины I уси­лителя. Поскольку Гsgl = N0lhv, в этом случае каждый возбужденный атом вынужденно испускает излучение и, таким образом, вносит свой вклад в энергию пучка. Такое условие, очевидно, соответствует наиболее эффектив­ному преобразованию запасенной энергии в энергию пучка, и поэтому во всех тех случаях, в которых это практически осуществимо, целесообразно использовать конструкции усилителей, работающие в режиме насыщения.

Следует вновь обратить внимание, что все приведенные выше уравнения рассматривались для усилителя, работающего по четырехуровневой схеме. В случае квазитрехуровневой схемы, согласно рассуждениям, приведенным в разделе 7.2.2, можно видеть, что уравнение (12.3.1) все еще применимо, если записать величину Г8 в виде:

Г e = ftv/(ae + ae), (12.3.15)

Где оеиоа — эффективные сечения вынужденного излучения и поглощения соответственно. Кроме того, нетрудно видеть, что уравнение (12.3.9) также применимо, если заменить величину а на Ge. Отсюда следует, что выражение

(12.3.12) остается справедливым в случае, когда величина Г8 определяется формулой (12.3.15) и когда G0 определяется как G0 = exp Аналогичное

Рассуждение можно провести и для усилителя, работающего по четырех­уровневой схеме, когда длительность импульса становится намного меньше времени жизни нижнего уровня перехода. В этом случае населенность ниж­него уровня, формируемая за счет вынужденного излучения, остается на этом уровне в течение всего импульса, отсюда можно видеть, что выражение

(12.3.12) все еще остается справедливым, если заменить величину о на <зе и записать Г8 через соотношение (12.3.15), где оа — эффективное сечение по­глощения нижнего уровня.

В случае, если усилитель обладает потерями, рассмотренная выше кар­тина несколько изменяется. В частности, плотность выходной энергии Г(/) теперь не увеличивается непрерывно с ростом входной (как это показано на рис. 12.2), а достигает максимума и затем уменьшается. Это можно понять, если заметить, что выходная плотность как функция длины усилителя име­ет тенденцию увеличиваться линейно за счет усиления (по крайней мере, при больших входных плотностях энергии, см. выражение (12.3.14)) и спа­дать экспоненциально за счет потерь (из-за члена - аГ в(12.3.11)). Конкурен­ция этих двух величин дает максимальное значение выходной плотности энергии Г. В случае, когда а £, это максимальное значение выходной плот­ности энергии Гт записывается в виде:

Гт = ёГ8/а. (12.3.16)

Однако следует отметить, что поскольку усилитель, как правило, обладает небольшими потерями, максимальное значение плотности энергии, которое можно получить от усилителя, ограничивается другими явлениями. В дейст­вительности, плотность энергии ограничивается значением Г^, при котором разрушается среда усилителя (в некоторых практических случаях этот порог разрушения составляет 10 Дж/см2 для ряда твердотельных активных сред). Таким образом, из выражения (12.3.14) получаем следующее условие:

Г = ё1Г8<Га. (12.3.17)

Другим ограничивающим фактором является то, что ненасыщенный коэф­фициент усиления (70 = ехр(а^) нельзя делать слишком большим, поскольку в таком случае в усилителе могут возникнуть два таких нежелательных эффекта, как паразитная генерация и усиленное спонтанное усиление (УСИ). Паразит­ная генерация возникает, когда усилитель начинает генерировать вследствие внутренней обратной связи, которая (в некоторой степени) всегда имеет место (например, благодаря наличию отражений на торцах усилителя). Явление УСИ уже обсуждалось в разделе 2.9.2. Оба этих явлений имеют тенденцию снимать имеющуюся инверсию населенностей и вследствие этого уменьшать усиление лазера. Чтобы свести к минимуму паразитную генерацию не следует использо­вать усилители большой длины. В идеальном случае усилитель должен иметь приблизительно одинаковые размеры во всех направлениях. Однако даже в этом случае паразитная генерация устанавливает верхний предел (ё1)тах Для произ­ведения коэффициента усиления # на длину усилителя I, т. е.

§1 < (^)шах, (12.3.18)

Где величина (^)шах обычно выбирается в диапазоне 3-5. Что касается поро­га для УСИ, его значение определялось в разделе 2.9.2 (см. выражение (2.9.4а) для лоренцевой линии). Если среда усилителя имеет форму куба (т. е. когда О = 1) и квантовый выход флюоресценции принимается равным единице, то в этом случае имеем <2 = 8 (или ё1 = 2,1), т. е. величину того же порядка, что и величина, определяемая паразитной генерацией. При меньших значениях телесного угла О (что обычно имеет место) величина О, определяющая начало действия УСИ, увеличивается (см. выражение (2.9.4а)). Следовательно, дос­тижение максимально возможного коэффициента усиления определяется, как правило, паразитной генерацией, а не явлением УСИ. Учитывая отмеченные ограничения, связанные как с разрушением среды усилителя (12.3.17), так и с паразитной генерацией (12.3.18), нетрудно получить выражение для макси­мальной энергии Ет, которую можно выделить из усилителя:

Ет^ТаЦ^ТаМ/ё2, (12.3.19)

Где 1т — максимальный размер усилителя (для кубической формы), опреде­ляемый формулой (12.3.18). Из выражения (12.3.19) следует, что величи­на Ет увеличивается с уменьшением коэффициента усиления g, а уменьше­ние последнего, в конечном счете, ограничивается потерями усилителя а.

Пример 12.2. Максимальная энергия, которую можно выделить из усилителя. Предположим, что максимальное значение gl ограничено па­разитной генерацией, так что (^)тах =10. Предположим также, что коэф­фициент усиления выбирается достаточно небольшим, ц = 10-2 см-1. При­нимая порог разрушения усилителя равным = 10 Дж/см2, из выраже­

Ния (12.3.19) находим Ет* 1 МДж. Однако при этом размер усилителя должен быть порядка 1т = (gl)m/g = 3 м, что весьма затруднительно реали­зовать на практике.

До сих пор в данном разделе обсуждалось изменение энергии лазерного импульса при его прохождении через усилитель. Однако в режиме насыщения существенным изменениям подвергаются также временное и пространствен­ное распределения входного пучка. Пространственные искажения нетрудно объяснить с помощью рис. 12.2. В случае, когда профиль интенсивности вход­ного пучка в поперечном сечении имеет колоколообразную форму (например, гауссов пучок), центральная область пучка вследствие насыщения будет уси­ливаться меньше, чем периферическая. Таким образом, по мере того как пучок проходит через усилитель, ширина его пространственного распределения в по­перечном сечении будет увеличиваться. Также нетрудно показать, почему пу­чок испытывает и временные искажения. Вынужденное излучение, вызванное передним фронтом импульса, приводит к тому, что к моменту появления зад­него фронта импульса из усилителя была уже извлечена некоторая часть запа­сенной энергии. Таким образом, когда задний фронт импульса проходит через усилитель, инверсия населенностей в усилителе оказывается ниже и, следова­тельно, пучок здесь испытывает меньшее усиление. Таким образом, в задний фронт импульса вкладывается меньше энергии, чем в передний, что ведет к довольно заметному изменению формы импульса. Форму выходного импульса можно вычислить из выражения (12.3.10), откуда можно показать, что в зави­симости от формы входного импульса выходной импульс может либо расши­риться, либо сузиться (или даже остаться неизменным) [7].