ПРИНЦИПЫ ЛАЗЕРОВ

ПО ЛУК ЛАССИЧЕСК АЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ ИЗЛУЧЕНИЯ. С ВЕЩЕСТВОМ

В последующих расчетах для описания взаимодействия излучения с вещест­вом будем использовать полуклассическую теорию. В этой теории атомная систе­ма предполагается квантованной (и, следовательно, описываемой законами кван­товой механики), а электромагнитное поле падающей волны рассматривается классически (т. е. с помощью уравнений Максвелла).

Сначала займемся изучением явления поглощения. С этой целью рассмотрим обычную двухуровневую систему и предположим, что в момент времени £ = О атом находится в основном состоянии 1 и что с ним взаимодействует монохроматиче­ская электромагнитная волна на частоте со. С классической точки зрения, атом в результате взаимодействия с электромагнитной волной приобретает дополнитель­ную энергию//'. Например, это может произойти при взаимодействии электри­ческого дипольного момента атома це с электрическим полем Е электромагнит­ной волны (Н' = меЕ). В данном случае будем говорить об электрическом диполь - ном взаимодействии. Однако это не единственный вид взаимодействия, благодаря которому может произойти переход. Например, переход может осуществиться вследствие взаимодействия магнитного дипольного момента атома с магнит­ным полем В электромагнитной волны (Н' = цтВ при магнитном дипольном взаи­модействии). Чтобы описать временную эволюцию этой двухуровневой системы, необходимо обратиться к квантовой механике. Иными словами, если классиче­ское рассмотрение работает с энергией взаимодействия Н то квантовомеханиче­ский подход вводит гамильтониан взаимодействия. Вид этого гамильтониана можно найти из классического выражения для энергии Н1' с помощью хорошо известных правил квантовой механики. Однако в данном случае точный вид вы­ражения для гамильтониана ТС не важен. Следует лишь заметить, что гамильто­ниан Н' является синусоидальной функцией времени, частота со которой равна частоте падающей волны. Таким образом, имеем

Н' = 7/о8Иш£. (А.1)

Тогда полный гамильтониан для атома Нможно записать в виде:

П=П0+Н, (А. 2)

Где 7/0 — гамильтониан атома в отсутствие электромагнитной волны. Если для моментов времени £ > О полный гамильтониан Низвестен, то зависимость волно­вой функции |/ атома от времени можно найти из нестационарного уравнения Шрёдингера:

^ = уй^. (А-3)

Для того чтобы решить это уравнение относительно функции введем в рассмотрение, согласно (2.3.1), невозмущенные собственные функции состояний 1 и 2 соответственно, а именно: функции = щех^-ЦЕ^/Н] и у2 = ы2ехр[-(/Е2£/7г)]. При этом функции щ и и2 должны удовлетворять стационарному уравнению Шрё - дингера:

TOC o "1-5" h z Н0щ = Еьщ(1 = 1, 2). (А.4)

С учетом влияния электромагнитной волны волновую функцию атома можно записать в виде:

V = аЛ*)»)/! + а2(*)1|/2, (А. 5)

Где ах и а2 — зависящие от времени комплексные числа, которые, согласно кван­товой механике, подчиняются следующему соотношению:

ах2 + а22 = 1. (А.6)

Так как, согласно (1.1.6), справедливо выражение ¥12 = =

= с2|а2(£)|2/с&, то необходимо вычислить величину |а2(£)|2. В общем случае вместо (А. 5) следует писать:

Т т

V = ехр[-ДЕ* /й)* ], (А. 7)

1 1

Где к обозначает состояние атома, а т — число состояний. Подставляя это выра­жение в уравнение Шрёдингера (А. З), получаем:

£(7*Ь+7*")а*ы*ехр [~](Ек/кЩ = ^{М<1ак/сН)икехр [}{Ек/ПЩ +

* * (А.8)

+акикЕкехр [~](Ек/ПЩ).

С помощью (А.4) это уравнение приводится к виду:

^№Шк/(1г)икехр [-;(£*/й)*] = £а*7*Хвхр [-/'(£*/Й)*]. (А-9)

Умножая обе части последнего уравнения на произвольную собственную функ­цию и*п и интегрируя по объему, получаем

^М(1ак/(И)ехр [-ХЕк/НЩ$ики*(1У =

5>*ехр [~КЕк/Пти; 'икйУ. (АЛ0)

Поскольку волновые функции ик ортогональны (т. е. [и*икбУ = Ъкп),то из УРав‘ нения (А. 10) получаем:

№пМ) = ^£,Я>*ехр [-■/—

Где Н’пк=Н'пк(1;) задается выражением

Н'пка) = и'пН'икйУ. (А.12)

Таким образом, имеем тп дифференциальных уравнений для т переменных аА(£), и эти уравнения можно решить, если только известны начальные условия.

Для двухуровневой системы волновая функция у, задаваемая (А.5) и (А. 11), оп­ределяется двумя уравнениями:

	(E2-El)t 1 h
(А. 13а)
(A. 136)
Которые должны решаться с начальными условиями а^О) = 1 и а2(0) = 0. До сих пор не делалось никаких приближений. Чтобы упростить процедуру решения уравнений (А.13), будем использовать метод возмущений. Предполо­жим, что в правой части уравнений (А.13) можно приближенно записать ахЦ) = 1 и а2(£) = 0. Решая уравнения (А.13) с учетом такого предположения, находим ре­шения для ах{Ь) и а2(*) в приближении первого порядка. По этой причине разви­ваемая далее теория называется теорией возмущений первого порядка. Решения а!(£) и а2(£), полученные таким образом, можно подставить теперь в правую часть уравнений (А.13), чтобы найти решение в приближении второго порядка, и т. д. до более высоких порядков. Таким образом, в первом порядке теории возмуще­ний уравнения (А.13) дают:
Da Dt
(А.14а)
|#21вхр (j<Ј>0t),
(A. l 46)
Где ю0 = №2 “ — частота перехода атома. Чтобы вычислить вероятность пе­ Рехода, достаточно решить лишь уравнение (А. 146). С этой целью воспользуемся выражениями (А.1) и (А. 12) и запишем ^=Я2>ш^ = ^[ехр (МЬвхр (-МИ (АЛ5) Где дается выражением Я2°1 = 1Ы2 № (А. 16) И является, вообще говоря, комплексной величиной. Подставляя (А. 15) в (А. 146) и интегрируя с учетом начального условия а2(0) = 0, получаем:
Ехр (-/Аса*)-! Дсо
(А. 18)
Где Асо = со - со0. Таким образом,
(А.19)

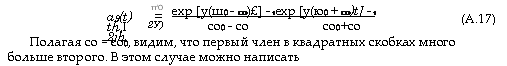Функция!/ = [Бт(Асо^/2)/Асо]2 построена на рис. А.1 в зависимости от Асо. Вид­но, что с увеличением времени соответствующая кривая становится все более узкой, а ее максимальное значение возрастает. Кроме того, поскольку, как мож­но показать, _

2

(А. 20)

То для достаточно больших значений £ можно положить

Г 8ш(Асэ£/2)12

= - у6(До>),

Где через 5 обозначена 6-функция Дирака. С учетом этого приближения из (А.19) получаем

I Н'° I2 - гг

102(01- д2 ^5(ДЮ). (А. 22)

Это выражение показывает, что при достаточно большом интервале времени, прошедшего после начала взаимодействия, вероятность |а2(£ )|2 обнаружить атом в момент времени £ на уровне 2 пропорциональна длительности этого интервала. Следовательно, вероятность перехода 1У12 дается выражением

И, и = ліМіЕ=|.И£г(іш).

Цля того чтобы вычислить У12 в явном виде, необходимо найти величину 12х| • Будем предполагать, что за переход ответственно взаимодействие между электрическим полем электромагнитной волны и электрическим дипольным мо­ментом атома (электрическое дипольное взаимодействие). Если г — радиус-вектор совершающего переход электрона по отношению к ядру, а е — величина заряда электрона, то классический дипольный момент атома будет равен це = - ег. Тогда классическая энергия взаимодействия/Г дается выражением 1~С = цеЕ = - еЕ(г, £) • г, где Е — электрическое поле падающей электромагнитной волны в точке, где на­ходится электрон. Теперь, пользуясь известными правилами квантовой механи­ки, нетрудно записать гамильтониан взаимодействия:

К = - еЕ(г, 0 • г. (А. 24)

Подставляя это выражение в (А.12) при п = 2 и к = 1, получаем:

Н'21 = - е г4Егщс1У. (А.25)

Предположим далее, что длина электромагнитной волны много больше раз­меров атома. Это условие очень хорошо выполняется для излучения в видимом

Диапазоне (для зеленого света X = 500 нм, в то время как размеры атома порядка -0,1 нм). С учетом такого предположения можно считать, что величина Е(г,/£) лишь незначительно меняется на атомном расстоянии, и в выражении (А.25)(ее можно вынести из-под интеграла, используя ее значение в точке г = 0, т. е. в цен­тре ядра (электрическое дипольное приближение). Таким образом, определим величину

Е(г, £) = Е(0, £) = Е08тсо£, (А.26)

Где Е0 — константа. Подставляя (А.26) в (А.25) и сравнивая полученное выраже­ние для #21 с (А. 15), находим, что величина Нможет быть выражена в виде:

Я£=Е0ц21, (А. 27)

Где ц21 равно

Ц21 = - и*2етщау. (А. 28)

Эта величина называется матричным элементом оператора электрического дипольного момента. Если через 0 обозначить угол между векторами 121 и Е0, то из (А.27) получим:

|#2°1|2 = Ео IЙ2112 сое2©. (А.29)

Здесь ||ы21| — модуль комплексного вектора ц21. Предположим, что электро­магнитная волна взаимодействует с несколькими атомами, векторы ц21 которых ориентированы произвольным образом относительно вектора Е0; тогда среднее значение величины кг получается усреднением выражения (А. 29) по всем воз­

Можным значениям углов 0 и ф (в двух измерениях). Если все углы 0 одинаково вероятны, то плотность вероятности р(0) не зависит от 0. В данном случае р(0) оп­ределяется таким образом, что р(0)сЮ есть элементарная вероятность для векто­ра ц21 оказаться внутри телесного угла <Ю, составляющего с направлением векто­ра Е0 угол 0. Известно, что если любой из углов 0 равновероятен, то (сое 20) = 1/3 (здесь угловые скобки означают усреднение по всем ориентациям диполей). Сле­довательно, . .

(|яй|) = £02|ц21|2/з. (А.30)

Последующая подстановка этого выражения в (А. 23) дает

Иги = я. (2я)^£|1ц21 125(ю _ Шо) (А>31)

Если вместо 6(со - со0) использовать в этом выражении б(у - у0), то оно преобра­зуется к выражению (2.4.5), поскольку 6(у - у0) = 2яб(со - со0).

Получив выражение для вероятности поглощения, перейдем теперь к расче­ту вероятности вынужденного излучения. Обратимся снова к уравнениям (А. 13), используя теперь другие начальные условия: а^О) = 0 и а2(0) = 1. Однако сразу можно заметить, что в данном случае необходимые соотношения получаются из соответствующих формул (А. 13) — (А.31), выведенных для случая поглощения, простой перестановкой индексов 1 и 2. Поскольку из определения (А.28) видно, что |ц12| = |ц21|, то из выражения (А.31) следует, что И^12 = ¥21, а это означает ра­венство вероятностей поглощения и вынужденного излучения.