ПАРАМЕТРИЧЕСКАЯ ГЕНЕРАЦИЯ
|
(12.4.29) |
![]() Рассмотрим теперь три волны с частотами сох, со2 и со3 (причем со3 = сох - I - со2), взаимодействующие в кристалле. Общее поле Е(г, £) этих волн можно записать в виде следующей суммы:
Рассмотрим теперь три волны с частотами сох, со2 и со3 (причем со3 = сох - I - со2), взаимодействующие в кристалле. Общее поле Е(г, £) этих волн можно записать в виде следующей суммы:
E(z, t) = Ещ (z, t) + (z, t) + Еаз (z, t),
Где каждое из полей определяется выражением (12.4.27а). Подставляя (12.4.29) в соотношение (12.4.2) и используя (12.4.27а), получаем выражение для компонент Р^ь(г) (аналогичное выражению (12.4.276)) нелинейной поляризации
на различных частотах со*. Выполнив утомительные, но несложные алгебраические преобразования, находим, что, например, компонента Р^ь(г) на частоте сох задается выражением:
Ргт =280<Щ}(2)Я2*(г)ехр [у№ - йз)2]. (12.4.30)
Компоненты нелинейной поляризации Рмь на частотах со2 и со3 вычисляются аналогичным образом. Подставляя в уравнение (12.4.28) компоненты величины Рмь9 соответствующие трем частотам, получаем следующие три уравнения:
|
Щс ) |
![]()
|
Щс) |
![]()
![]()
|
**!L = J - CT-L_ )e3 - j{ dz 2тцг0с) щс) |
![]()
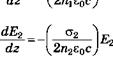
|
DE^E2exp [-j(k1-k2-k3)z. (12.4.31b) |
![]() DE3E2exp [—у(Д? з —k2~ki)z], (12.4.31а) dE3Ei exp [-j{k3-kl-k2)z, (12.4.316)
DE3E2exp [—у(Д? з —k2~ki)z], (12.4.31а) dE3Ei exp [-j{k3-kl-k2)z, (12.4.316)
Эти основные уравнения описывают нелинейное параметрическое взаимодействие. Нетрудно видеть, что они связаны между собой посредством нелинейного коэффициента d.
На данном этапе удобно определить новую переменную А* поля:
Л = (^М)1/2^. (12.4.32)
|
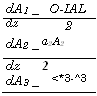 Поскольку интенсивность волны равна /* = п*е0с|2£*|2/2, соответствующий поток фотонов Ft можно записать в виде: Ft = Ii/focdi = (e0c/2/i)|Aj2. Таким образом, величина |At2 пропорциональна потоку фотонов Ft с частотой со*, причем коэффициент пропорциональности не зависит от nt и со*. В этих новых полевых переменных уравнения (12.4.31) принимают вид:
Поскольку интенсивность волны равна /* = п*е0с|2£*|2/2, соответствующий поток фотонов Ft можно записать в виде: Ft = Ii/focdi = (e0c/2/i)|Aj2. Таким образом, величина |At2 пропорциональна потоку фотонов Ft с частотой со*, причем коэффициент пропорциональности не зависит от nt и со*. В этих новых полевых переменных уравнения (12.4.31) принимают вид:
}А2* exp [-j(Akz)], (12.4.33а)
3Aiexp [-/(Ate)], (12.4.336)
LiA2exp [j(Akz), (12.4.33b)
Аг 2 —
Где а* = а*/я*е0с, Ак = к3-к2~к1и
И л1/2
8 = ^1 Ю10)2(03 1 . (12.4.34)
СуЩЩПз )
Преимущество использования А* вместо Еь очевидно, поскольку в противоположность уравнениям (12.4.31) в уравнения (12.4.33) теперь входит единственный параметр связи 5.
Пренебрегая потерями (т. е. полагая щ = 0), умножая обе части уравнения (12.4.33а) на А{, а обе части уравнения (12.4.336) на А2 и сравнивая полученные выражения, приходим к следующему соотношению: = -<2|А3|2/*йг.
Выполняя аналогичные преобразования уравнений (12.4.336) и (12.4.33в), получаем йА22/йг = ~(1Аг2/йг. Таким образом, можно записать следующие равенства:
|
ЙАх2 _(1А22 _ д? 1Л3 |2 |
![]() (1г йг йг 9
(1г йг йг 9
Которые называются соотношениями Мэнли-Роу. Поскольку величина |А*|2 пропорциональна соответствующему потоку фотонов, из соотношений (12.4.35) следует, что всякий раз, когда уничтожается фотон с частотой со3, образуются фотоны с частотами сох и со2. Это согласуется с фотонной моделью параметрического процесса, о которой говорилось в разделе 12.4.1.2. Следует заметить, что из соотношений (12.4.35) вытекает, например, следующее равенство: (с/Рх/с^г) = -(со1/со3)(^Р3/^г),где Рг и Р3 — мощности соответствующих волн. Таким образом, в излучение с частотой щ может быть преобразована лишь часть мощности излучения с частотой со3.
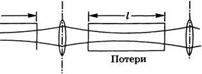
Строго говоря, уравнения (12.4.33) справедливы в случае «бегущей» волны, когда в кристалле произвольной длины распространяются три волны с частотами со15 со2, о>3. Покажем теперь, каким образом эти уравнения можно применить к случаю оптического параметрического генератора, схематически показанного на рис. 12.8. Рассмотрим сначала генератор, работающий по двухрезонансной схеме. В этом случае внутри резонатора в прямом и обратном направлениях распространяются две волны с частотами и со2. Параметрический процесс имеет место здесь только тогда, когда направления распространения этих волн и волны накачки совпадают (поскольку лишь при данных обстоятельствах удовлетворяется условие фазового синхронизма). Если «развернуть» оптический путь волны в резонаторе так, как показано на рис. 12.9а, то из рисунка видно, что волны испытывают потери на любом участке пути, в то время как параметрическое усиление имеет место лишь на одном из двух отрезков пути. Эту ситуацию можно эквивалентно представить в виде схемы, приведенной на рис. 12.96, если соответствующим образом определить коэффициент эффективных потерь а* (I = 1, 2). Потери, определяемые на рис. 12.96 длиной кристалла I, на самом деле должны быть равны потерям при двойном проходе резонатора, как показано на
|
I |
![]()
|
Потери зеркала 1 |
![]()
|
Потери + усиление |
![]()
Рис. 12.9
А) «Развертка» оптического пути в резонаторе ОПГ; б) приведение рассмотренной выше конфигурации к варианту однопроходной схемы, причем потери на зеркалах включены в распределенные потери в кристалле
|
----- 1----- ► |
—і |
|
|
1 |
||
|
Ч |
|
Потери Потери Зеркала 1 зеркала 2 |
|
Эффективные і потери + усиление : |
Рис. 12.9а. Последние представляют собой реальные потери в кристалле, а также потери, обусловленные дифракцией и отражением на зеркалах. Следовательно, входящие в уравнения (12.4.33) коэффициенты и а2 должн- быть определены таким образом, чтобы они учитывали эти различные потери. Из уравнений (12.4.33), пренебрегая параметрическим взаимодействием (т. е. полагая 6 = 0), можно видеть, что после прохождения пути I, равного длине кристалла, мощность излучения на частоте со* (I = 1, 2) уменьшается в ехр(-а*0 раз. При этом необходимо учитывать потери, которые испытывает излучение при двукратном проходе резонатора. Это требование можно записать следующим образом:
|
(12.4.35a) |
![]() Ехр(-аа) = RuR2i(l ~ Lt)2,
Ехр(-аа) = RuR2i(l ~ Lt)2,
Где Еи и Л21 — коэффициенты отражения (по мощности) соответствующих зеркал, а Ц — потери в кристалле (с учетом дифракционных потерь) за один проход излучения с частотой со*. Определим теперь следующие величины (ср. с (1.2.4)): уи = -1пД1г, у2; = -1пД2„ у2г =-1пЙ2г, у; =—1п(1-1-г)иу( =[(уц+у2</2]+у|. При этом выражение (12.4.35а) принимает вид:
|
= 2у„ |
![]() (12.4.36)
(12.4.36)
Где у* — общие потери в резонаторе (на частоте со*) за один проход. Заметим, что это равносильно замене потерь, обусловленных отражением от зеркал, потерями, распределенными по кристаллу, и последующему включению их в эффективный коэффициент поглощения а* (Ь = 1, 2) кристалла. При этом величина а3 учитывает лишь потери внутри кристалла, которыми, вообще говоря, можно пренебречь. Таким образом, на этом этапе можно утверждать, что в случае двухрезонансной параметрической генерации уравнения (12.4.33) все еще остаются справедливыми при условии, что а2 и а2 определяются выражением (12.4.36) и что а3 = 0.
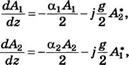 Чтобы получить пороговое условие для параметрической генерации в двухрезонансной схеме, приведем уравнения (12.4.33) к более простому виду, предположив, что «истощением» волны накачки за счет параметрического процесса можно пренебречь. Используя это предположение, а также предположение о том, что а3 = 0, можно положить А3(г) = А3(0), гдеА3(0) — амплитуда падающей волны накачки, которая считается вещественной. Если предположить затем, что Ак = 0 (идеальный фазовый синхронизм), то уравнения (12.4.33) принимают существенно более простой вид:
Чтобы получить пороговое условие для параметрической генерации в двухрезонансной схеме, приведем уравнения (12.4.33) к более простому виду, предположив, что «истощением» волны накачки за счет параметрического процесса можно пренебречь. Используя это предположение, а также предположение о том, что а3 = 0, можно положить А3(г) = А3(0), гдеА3(0) — амплитуда падающей волны накачки, которая считается вещественной. Если предположить затем, что Ак = 0 (идеальный фазовый синхронизм), то уравнения (12.4.33) принимают существенно более простой вид:
(12.4.37a)
|
Где |
![]() (12.4.376)
(12.4.376)
|
|
(12.4.38)
Теперь нетрудно получить пороговое условие для параметрической генерации при двойном резонансе. Для этого в уравнениях (12.4.37) поло
жим dAx/dz = dA2/dz = 0, что приводит к следующей системе однородных уравнений:
Oil Ах + jgA2 =0, (12.4.39а)
JgA1 - а 2А2 =0, (12.4.396)
Где в последнем уравнении левая часть является комплексно-сопряженной относительно правой части уравнения (12.4.376). При решении этой однородной системы уравнений ненулевые значения Ах и А2 имеют место лишь при условии
G2 = ага2 = 4 (т2/12). (12.4.40)
Последнее выражение получено с помощью соотношения (12.4.36). Следует отметить, что согласно (12.4.38), величина g2 пропорциональна величине Е3(0), т. е. интенсивности волны накачки. Таким образом, условие (12.4.40) означает, что для возбуждения параметрической генерации необходима определенная пороговая интенсивность волны накачки. Как будет показано в следующем примере, эта интенсивность пропорциональна произведению потерь (по мощности) у! и у2 двух волн с частотами coj и со2 за один проход в резонаторе и обратно пропорциональна величинам d2 ml2.
Пример 12.4. Расчет пороговой интенсивности пучка накачки в двухрезонансном оптическом параметрическом генераторе. Из соотношений
(12.4.38) и (12.4.40) нетрудно получить выражение для порогового значения величины Е3(0), которая представляет собой квадрат амплитуды поля пучка накачки:
Р2 /л - °2 п1п2 У1У2
|
![]() Поскольку интенсивность пучка накачки задается выражением /3 = = п3£0сЕ32/2, соотношение для пороговой интенсивности накачки можно записать в виде:
Поскольку интенсивность пучка накачки задается выражением /3 = = п3£0сЕ32/2, соотношение для пороговой интенсивности накачки можно записать в виде:
Г И ^ Г#- Мгч л ^ л Л
[У1Уг].
Где Z = 1/г0с = 377 Ом — полное электрическое сопротивление свободного пространства, и — длины волн «сигнальной» и «холостой» волны соответственно. Заметим, что член в правой части этого выражения, приведенный в первых квадратных скобках, имеет размерность интенсивности, таким образом, все остальные члены в квадратных скобках являются безразмерными.
Случай однорезонансной параметрической генерации является несколько более сложным. Если лазерный резонатор настроен лишь на частоту сох, то величину ах можно снова представить в виде (12.4.36). Поскольку волна на частоте со2 не отражается обратно в резонатор, величина а2 будет включать в себя только потери в кристалле и, следовательно, эту величину можно не учитывать. Опять пренебрегая «истощением» волны накачки и предполагая, что фазовый синхронизм является идеальным, уравнения (12.4.37)
можно применить и в этом случае, но при условии, что а2 = 0. В случае, когда параметрическое преобразование невелико, в правой части уравнения
(12.4.376) можно положить А{(г) = А{(0). Таким образом, имеем следующее выражение:
A2(z) = - jgAf(0)z/2, (12.4.41)
При выводе которого предполагалось, что А2(0) = 0 (т. е. из резонатора в кристалл волна на частоте со2 обратно не возвращается). Если подставить выражение (12.4.41) в (12.4.37а) и в правой части последнего положить Аг(г) = А^О), то можно записать следующее:
IH~f+Tb<o>- <12-4-42)
Интегрирование этого уравнения по длине кристалла I дает следующее выражение для амплитуды волны на частоте сох:
А (0 = А (0)^1 ~^Y+(12.4.43)
Пороговое условие достигается при Аг(1) = Ах(0), т. е. когда
G2 ='TL = l2L' (12.4.44)
Поскольку величина g2 пропорциональна интенсивности I волны накачки, сравнение выражений (12.4.44) и (12.4.40) дает отношение пороговых значений интенсивности накачки:
^- = — (12.4.45)
*DRO У2
(здесь индексы SRO и DRO обозначают однорезонансную и двухрезонансную генерацию соответственно). Если в качестве примера выбрать потери за проход равными у2 = 0,02 (т. е. 2%), то из выражения (12.4.45) находим, что пороговая мощность для однорезонансной генерации должна быть в 100 раз больше, чем для двухрезонансной.