ОПТИМАЛЬНАЯ СВЯЗЬ НА ВЫХОДЕ ЛАЗЕРА
При фиксированной скорости накачки существует некоторое значение коэффициента пропускания Т2 выходного зеркала, при котором достигается максимальная выходная мощность. Физически существование такого оптимума связано с тем, что с увеличением Т2 имеют место два следующих эффекта: 1) выходная мощность растет с увеличением коэффициента пропускания выходного зеркала; 2) выходная мощность должна уменьшаться, поскольку с увеличением пропускания возрастают внутрирезонаторные потери, что приводит к уменьшению числа фотонов ф0 в резонаторе.
Для определения оптимального условия связи на выходе лазера ограничимся схемой четырехуровневого лазера и рассмотрим пространственно независимую модель. Значение оптимального коэффициента пропускания выходного зеркала можно определить из выражения (7.3.9), потребовав выполнения условия с1Роиг/с1у2 = 0 при фиксированном значении мощности накачки Рр. При этом необходимо учитывать тот факт, что, согласно выражению (7.3.12), величина Р1П также является зависящей от у2. Из выражения (7.3.12) можно записать:
Где Ршк представляет собой минимальную пороговую мощность накачки й определяется как пороговая мощность накачки при нулевой связи на выходе, т. е. при пренебрежимо малых потерях у2 = 0. Выражение (7.3.9) может быть преобразовано в следующее соотношение:
|
Роиі — |
*т ^ (7.5.2)
8+1
И
Хт = Рр/РтгН - (7.5.4)
Единственным членом в выражении (7.5.2), зависящим от у2, является величина в, которая, согласно выражению (7.5.3), пропорциональна у2. Оптимальное условие связи на выходе можно получить, записав условие йРоШ/с18 = 0; при этом нетрудно получить оптимальное значение величины 5:
Соответствующее выражение для выходной мощности можно найти из выражения (7.5.2), т. е.
|
Р *ор |
ІМ1'2-!]2. (7.5.6)
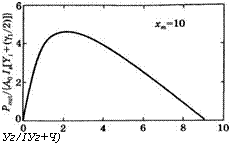
Уменьшение выходной мощности, обусловленное неоптимальными условиями генерации, оказывается наиболее важным вблизи порога генерации (т. е. когда хт = 1). Однако при значительных превышениях накачки над порогом генерации выходная мощность становится практически нечувствительной к изменению связи на выходе вблизи ее оптимального значения. Например, на рис. 7.15 приводится график зависимости нормированной выходной мощности Р0Ш от параметра 5 для случая хт = 10. Согласно выражению (7.5.2), выходная мощность Рои1 = 0 в случаях, когда 5 = 0 (т. е. при у2 = 0) и когда в = 9; далее, согласно выражению (7.5.5), можно найти, что Бор = 2,16. Из рис. 7.15 нетрудно видеть, что изменение параметра 5, т. е. изменение связи на выходе, вплоть до 50% относительно оптимального значения, приводит всего лишь к 5%-ному уменьшению выходной мощности.
|
Уг/ІУг+Ч) |
В случае пространственно-зависимой модели можно прибегнуть к аналогичным рассуждениям, взяв за основу выражение (7.3.29) для однородной накачки или выражение (7.3.34) для гауссова профиля накачки. Однако следует отметить, что при значительном превышении накачки над порогом генерации связь между выходной мощностью и мощностью накачки становится линейной (см. рис. 7.11), как это было видно из выражения (7.3.9).
Рис. 7.15
График зависимости нормированной выходной мощности РоШ от нормированного коэффициента пропускания выходного зеркала у2 для случая, когда мощность накачки Рр превышает минимальное пороговое значение Рш/1 в 10 раз
Учитывая относительную нечувствительность параметра РоШ к изменению связи на выходе (относительно оптимального значения) можно также приближенно использовать для этого случая выражение (7.5.5), где параметр Рш}1 в данном случае определяется из выражения (7.3.26) для однородной накачки или из выражения (7.3.32) для гауссова профиля накачки, используя запись у = у* + (ух/2).
Пример 7.6. Оптимальная связь на выходе АС лазера с оптической накачкой. Рассмотрим конфигурацию лазера, которая обсуждалась в примере 7.2 (см. рис. 7.4. и 7.5), и рассчитаем оптимальное значение коэф-
Фициента пропускания выходного зеркала в случае, когда входная мощ-
Ность лампы накачки составляет Рр = 7 кВт. Поскольку пороговая мощность Pth, исходя из рис. 7.5, составила 2,2 кВт, то согласно выражению (7.5.1) при Ух = 0 получаем Pmth = Р*Л(у*/у) «697 Вт, где у* = 0,038 и у = 0,12 получены в примере 7.2 и представляют собой внутренние и полные потери соответственно. Далее имеем хт = Pp/Pmth « 10, и, таким образом, из выражения (7.5.5) получаем Sop «2,17. Используя выражение (7.5.3), окончательно получаем значение (y2)0jP ~ 0,165, которое соответствует оптимальному коэффициенту пропускания зеркала (Т2)ор = 1 - ехр [-(Уг)ор] * 15%, что достаточно хорошо согласуется с результатом, рассмотренным на рис. 7.6.
