ОДНОРОДНОЕ УШИРЕНИЕ
Первый из рассматриваемых механизмов однородного уширения линий связан со столкновениями и называется столкновительным уширением. В газах он реализуется при столкновениях атома с другими атомами, ионами, свободными электронами и т. д., либо со стенками сосуда. В твердых телах он обусловлен взаимодействием атома с фононами решетки. В результате столкновения волновые функции у1 и |/2 для двух уровней атома (см. (2.3.1)) испытывают случайный скачок фазы. Это означает, что фаза осциллирующего дипольного момента ь08С (см. (2.3.6)) также претерпевает случайный сдвиг относительно фазы падающей электромагнитной волны. Таким образом, эти столкновения прерывают процесс когерентного взаимодействия излучения
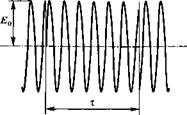
Рис. 2.9 Изменение во времени напряженности электрического поля электромагнитной волны ЕЦ), воспринимаемое атомом, испытывающим столкновения. (Реально за время между столкновениями т может произойти 107 или более колебаний.)
 С атомом. Поскольку именно относительная фаза имеет значение при этом взаимодействии, то теоретическое описание ситуации не изменится, если предположить, что сдвиг при каждом столкновении испытывает фаза напряженности электрического поля, а не фаза дипольного момента х08С. В результате, напряженность электрического поля не может более считаться синусоидально изменяющейся во времени величиной, а будет иметь вид, представленный на рис. 2.9, где каждый скачкообразный сдвиг фазы связан со столкновением. Понятно, что при таких условиях атом уже не воспринимает электромагнитную волну как монохроматическую. В этом случае, записав объемную плотность энергии излучения в узком спектральном интервале от у' до у' 4- (IV в виде йр = Ру^у', можно подставить эту величину в соотношение, справедливое для монохроматического излучения, т. е. в (2.4.7), что приводит к выражению:
С атомом. Поскольку именно относительная фаза имеет значение при этом взаимодействии, то теоретическое описание ситуации не изменится, если предположить, что сдвиг при каждом столкновении испытывает фаза напряженности электрического поля, а не фаза дипольного момента х08С. В результате, напряженность электрического поля не может более считаться синусоидально изменяющейся во времени величиной, а будет иметь вид, представленный на рис. 2.9, где каждый скачкообразный сдвиг фазы связан со столкновением. Понятно, что при таких условиях атом уже не воспринимает электромагнитную волну как монохроматическую. В этом случае, записав объемную плотность энергии излучения в узком спектральном интервале от у' до у' 4- (IV в виде йр = Ру^у', можно подставить эту величину в соотношение, справедливое для монохроматического излучения, т. е. в (2.4.7), что приводит к выражению:
** "■ ................................. (2.5.1)
|
Й¥12 = |
![]() ІН-2112 Р^(у'-у0)<*у'.
ІН-2112 Р^(у'-у0)<*у'.
3 п2г0к2
Полная вероятность перехода получается путем интегрирования соотношения (2.5.1) по всему спектру частот излучения, что дает:
SHAPE \* MERGEFORMAT ![]()
|
(2.5.2) |
![]()
2п2
Щ9=-
12 3 п2г0к2
Теперь можно записать ру, в виде:
+00
ІЦ21І2 |рУ'8(у'-у0)^у'.
Ру’=Р£(у'-у), (2.5.3)
Где р — плотность энергии волны в единице объема (см. соотношение (2.4.6)), а функция #(у' - у) описывает спектральную зависимость величины ру.. Поскольку, очевидно, р = |ру'<2у', то интегрирование обеих частей выражения
(2.5.3) показывает, что функция #(у' - у) должна удовлетворять условию нормировки +00
|
(2.5.4) |
Подставляя (2.5.3) в соотношение (2.5.2) и используя хорошо известные математические свойства 8-функции, получим:
(2.5.5)
Как и предсказывалось в разделе 2.4.1, видно, что величину 1У12 действительно можно получить путем замены 8(у - у0) в соотношении (2.4.7) на £(у - у0). Отметим, что согласно (2.5.4) справедливо также равенство
+00
|я(у-у0)сгу = 1. (2.5.6)
-оо
Теперь остается рассчитать нормированную функцию спектральной плотности энергии падающего излучения £(у' - у). Эта функция зависит от длительности интервала времени х между двумя последовательными столкновениями (рис. 2.9), которая, очевидно, отличается от столкновения к столкновению. Предположим, что распределение величин х можно описать плотностью вероятности
При этом рх(1 х является вероятностью того, что длительность интервала времени между столкновениями находится в диапазоне от х до х 4- йх. Отметим, что параметр хс в (2.5.7) имеет физический смысл среднего интервала времени между двумя последовательными столкновениями, (х). Действительно, легко видеть, что
|
(2.5.8) |
![]() (т) = |тртйх = 1
(т) = |тртйх = 1
На данном этапе математическая задача, которую требуется решить, четко определена. Необходимо рассчитать нормированную спектральную плотность энергии электромагнитной волны, изображенной на рис. 2.9, для которой длительность интервала времени х между столкновениями имеет статистическое распределение^, задаваемое соотношением (2.5.7). Сославшись, в плане математических деталей, на Приложение Б, просто приведем здесь окончательный результат. Искомая нормированная спектральная функция определяется соотношением
В соответствии с (2.5.5) форму контура линии перехода можно получить из
(2.5.9) путем замены у' на у0. При этом имеем:
^(У “Уо) = 2Тс [Г+ 4я*т|1(у - у0)2] ’ (2.5.10)
Что и является требуемым окончательным результатом. Таким образом, получаем функцию лоренцевой формы (см. рис. 2.6), в общем виде описываемой соотношением (2.4.8), в котором значение в максимуме равно теперь 2хс, а параметр Ау0 является столкновительной шириной линии, равной
Ау0 = 1 /пхс. (2.5.11)
Пример 2.2. Столкновительное уширение линии в Не-Ие лазере. В качестве первого примера столкновительного уширения рассмотрим переход атома или иона в газе при давлении р. Оценка тс дается в этом случае величиной тс = где I — средняя длина свободного пробега атома в газе, а
— его средняя тепловая скорость Учитывая, что = (3кТ/М)1/2, где
М — масса атома, и выбирая I равной величине, определяемой моделью
|
(2.5.12) |
![]() Твердых сфер, получаем:
Твердых сфер, получаем:
|
|
Где а — радиус атома, ар — давление газа. Для газа атомов Ne при комнатной температуре и давлении р = 0,5 Topp (типичном давлении для He-Ne лазера), используя (2.5.12), в котором а = 0,1 нм и гс = 0,5мкс, находим из (2.5.11), что Av0 = 0,64 МГц. Отметим, что величина тс обратно пропорциональна, и, следовательно, величина Av0 прямо пропорциональна давлению р. В качестве эмпирического правила можно принять, что по порядку величины для любого атома столкновения дают вклад в уширение линии перехода, примерно равный (Av0/p) = 1 МГц/Topp и сравнимый с тем, что получился для атомов Ne. Отметим также, что число периодов электромагнитной волны, укладывающихся на интервале времени между столкновениями тс, равно m = vxc. Для волны, частота которой попадает в середину видимого диапазона, имеем v = 5 • 1014 Гц, так что указанное число периодов равно 5 • 108. Это подчеркивает тот факт, что рис. 2.9 сделан не в масштабе, поскольку реальное число колебаний за время т во много раз больше, чем изображено на рисунке.
Пример 2.3. Ширина линии в кристаллах рубина и Nd:YAG. В качестве другого примера столкновительного уширения рассмотрим переход примесного иона в ионном кристалле. В этом случае происходят столкновения фононов решетки с ионом. Поскольку число фононов в данной колебательной моде решетки сильно зависит от температуры, то можно ожидать, что ширина линии перехода будет иметь значительную температурную зависимость. В качестве примера на рис. 2.10 приведена зависимость ширины линии от температуры как в кристалле Nd:YAG, так и в кристалле рубина. Ширина линии здесь выражена в волновых числах (см-1) — единицах, которые используются спектроскопистами гораздо чаще, чем обычные единицы частоты.[10] Видно, что при 300 К ширина линии лазерного перехода равна Av0 = 4 см-1 = 120 ГГц — для кристалла Nd:YAG и Av0 =11 см1 = 330 ГГц — для кристалла рубина.
Второй механизм однородного уширения линий связан с явлением спонтанного излучения. Поскольку такое излучение характеризуется только
Свойствами данного перехода, то соответствующее уширение называют естественным, или собственным. В случае естественного уширения проще всего рассматривать его проявления на примере спектра испускания излучения. Отметим, что, как указывалось в разделе 2.3.2, спонтанное излучение — это чисто квантовое явление, т. е. его можно корректно описать только при квантовании как вещества, так и излучения. Отсюда следует, что корректное описание спектрального контура испускаемого излучения также требует кван - тово-электродинамического подхода. Ограничимся поэтому приведением конечного результата, который оказывается очень простым, и обсуждением его с использованием некоторых простых соображений. Квантово-электродинами - ческая теория спонтанного излучения [10] показывает, что спектральная функция £(у - у0) снова представляет собой лоренцев контур, вид которого может быть получен из соотношения (2.5.10) путем замены параметра тс на 2х8р9 где
|
Температура [К] Рис. 2.10 Температурная зависимость ширины линии лазерного перехода, определяемой уширением за счет фононов, в кристаллах рубина и ЫсЬУАО |
![ОДНОРОДНОЕ УШИРЕНИЕ подпись:
температура [к]
рис. 2.10 температурная зависимость ширины линии лазерного перехода, определяемой уширением за счет фононов, в кристаллах рубина и ысьуао](/img/655/image106.gif) Х8р — излучательное время жизни. Так, в частности, естественная ширина линии перехода (ЕА¥НМ) равна
Х8р — излучательное время жизни. Так, в частности, естественная ширина линии перехода (ЕА¥НМ) равна
Ау0 = 1/2пх8р. (2.5.13)
Для того чтобы убедиться в правильности этого результата, отметим, что поскольку мощность, излучаемая атомом, спадает со временем как ехр(^/х8р), то можно предположить, что напряженность соответствующего электрического поля изменяется согласно соотношению Е^) = ехр(^/2х8р) cos(o0t. Получаемая тогда зависимость от времени мощности излучения (которая пропорциональна (Е2(£)))> а именно ехр(-£/т8р), будет корректно отражать закон ее спадания. Теперь нетрудно рассчитать спектральное распределение, отвечающее такой временной зависимости напряженности поля Е(£), и убедиться, что контур линии является лоренцевым, а его ширина определяется соотношением (2.5.13).