НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ С ЗЕРКАЛОМ С ПЕРЕМЕННЫМ КОЭФФИЦИЕНТОМ ОТРАЖЕНИЯ
Некоторые, если не все, недостатки неустойчивых резонаторов с резкой границей зеркала можно исправить, используя неустойчивые резонаторы с зеркалом с переменным коэффициентом отражения. В этом случае коэффициент отражения зеркала на выходе, вместо того чтобы равняться 1 при г < а2 и нулю при г > а2, как у резонатора с резкой границей зеркала, уменьшается по радиусу от максимальной величины И0 в центре вплоть до нуля на расстоянии, сравнимом с поперечным размером активной среды [14]. Обозначим через р(г) коэффициент отражения зеркала 2 по напряженности поля и рассмотрим односторонний резонатор с коэффициентом увеличения за обход М. Для простоты используем подход, основанный на геометрической оптике. Используя в качестве координаты расстояние г от оси резонатора вдоль радиуса, можно представить, что напряженность и2(Мг) электрического поля волны, проходящей после одного обхода через точку с координатой Мг на зеркале 2, определяется напряженностью и2(г)*поля волны, падающей на зеркало 2 в точке с координатой г в начале обхода. Учитывая коэффициент отражения по напряженности зеркала 2 и коэффициент увеличения за обход М, можно записать, что
4(Мг)-Й2й£>. (5.6.6)
Появление величины М в знаменателе в правой части выражения (5.6.6) нетрудно объяснить тем, что после М-кратного увеличения площадь пучка увеличивается в М2 раз. При неизменной мощности в пучке его интенсивность должна уменьшиться в М2, а напряженность электрического поля — в М раз.
Если функция и2 отвечает моде резонатора, то должно выполняться соотношение и2(г) = аи2(г), в котором а является действительной величиной, по модулю меньшей 1, что связано с наличием в резонаторе потерь. Из (5.6.6) получаем:
Ст“2(Мг)----------- м----- ' (5.6.7)
Собственные функции и2(г) = и21(г) уравнения (5.6.7) определяют распределения напряженности электрического поля внутри резонатора перед зеркалом 2. При этом собственные значения этого уравнения определяют потери за обход, обусловленные выходом излучения, в соответствии с известным соотношением (см. (5.2.6)):
У = 1 — а2. (5.6.8)
Рассмотрим вначале случай гауссового профиля коэффициента отражения зеркала на выходе резонатора [11, 12]. Запишем коэффициент отражения этого зеркала в виде:
Р = р0ехр(-г2/и4), (5.6.9)
Где р0 — коэффициент отражения в максимуме, а параметр wm задает поперечный масштаб изменения профиля коэффициента отражения. Отметим, что в соответствии с (5.6.9) профиль коэффициента отражения по энергии, величина которого обычно измеряется в эксперименте, имет вид:
R = До exp(-2r2 /wl), (5.6.10)
Где Rq = pg — коэффициент отражения по энергии в максимуме. Используя соотношение (5.6.9) путем непосредственной подстановки можно показать, что решение уравнения (5.6.7) низшего порядка имеет вид:
“2о(/'> = UaoCOJexpt-r2/^2), (5.6.11)
|
(5.6.12) |
![]() ГДе W2 = (М2 -1 )Wm.
ГДе W2 = (М2 -1 )Wm.
Соответствующее собственное значение а равно
G = Po/M, (5.6.13)
Так что согласно (5.6.8) потери, обусловленные выходом излучения, равны
У=1-(Д0/М2). (5.6.14)
Радиальный профиль интенсивности пучка, падающего на зеркало 2, определяется соотношением:
Iin(r) = iin(0)exp (-2Г2 / w2). (5.6.15)
Видно, что радиальные профили как амплитуды напряженности электрического поля и2о, так и интенсивности Iin пучка описываются функцией Гаусса. С другой стороны, радиальный профиль интенсивности выходящего пучка Iout определяется выражением
Ioutir) = Iin(r)[ 1 - Д(г)] = /*Л(0)[ехр (~2r*/w2) - R0exр (-2MV/h;2)], (5.6.16)
Для получения которого были использованы соотношения (5.6.15), (5.6.10) и (5.6.12). Отметим, что радиальное распределение Iout не описывается функцией Гаусса и при определенных условиях можно ожидать, что этот профиль будет иметь плоскую вершину при г = 0, что представляет интерес с точки зрения некоторых приложений. Действительно, это может иметь место, если выполняется условие (d2Iout/dT2,)r=={i = 0. Из выражения (5.6.16) находим, что для этого коэффициент отражения R0 в центре зеркала и коэффициент увеличения М должны быть связаны соотношением
RqM2 = 1. (5.6.17)
Потери за обход в этом резонаторе, согласно (5.6.14) и (5.6.17), даются величиной
У =1 - (1/М2). (5.6.18)
Приведенные соотношения являются основными результатами для неустойчивых резонаторов с гауссовыми профилями коэффициентов отражения зеркал. Хотя эти результаты получены на основе простых рассуждений в рамках геометрической оптики, при относительно больших значениях
эквивалентных чисел Френеля (ЛГС9 ^ 5) они хорошо согласуются с расчетами, использующими методы волновой оптики [15]. Для зеркал с гауссовыми профилями коэффициентов отражения изящный анализ в рамках волновой оптики можно также провести, взяв за основу соответствующую комплексную АВС1)-матрицу [16].
|
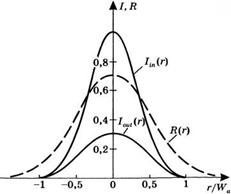
Рис. 5.23 Радиальные профили интенсивности внутри (Ііп) и снаружи (1ои1) неустойчивого резонатора с гауссовым профилем коэффициента отражения Щг) зеркала на выходе (случай поперечного профиля 1ои1 с плоской вершиной) |
 Пример 5.11. Расчет неустойчивого резонатора с зеркалом на выходе, имеющим гауссов профиль коэффициента отражения. Положим у = 0,5, исходя из того, что эта величина оптимизирует мощность излучения на выходе из данного лазера (см. главу 7), и рассмотрим случай, когда поперечный профиль пучка на выходе имеет плоскую вершину. Из (5.6.18) получаем М2 = %/2, из (5.6.17) имеем До=1/М2=1/л/2=0,71, а (5.6.12) дает а’2 =0,41 Радиальные профили коэффициента отражения зеркала на выходе и интенсивности излучения внутри и снаружи резонатора показаны на рис. 5.23. Обозначим теперь через а радиус активной среды и будем считать, что она находится непосредственно перед зеркалом 2, а радиальный профиль интенсивности пучка в среде описывается функцией 1т(г). Для того чтобы избежать излишнего виньетирования пучка апертурой активной среды, т. е. чтобы избавиться от обусловленных таким виньетированием ярко выраженных дифракционных колец, можно, например, наложить условие, что11п(а)/11п(0) = 2 • 10-2. Получим при этом а = 0,9и)т, что для данного размера апертуры а определяет величину характерного параметра ют гауссова профиля коэффициента отражения. Например, если положить а = 3,2 мм, то получим, что шт = 3,5 мм. Таким образом, гауссово зеркало должно иметь максимальный коэффициент отражения Д0 = 71%, характерный параметр профиля ьит = 3,5 мм и быть установлено в неустойчивом резонаторе (например, конфокальном) с увеличением за обход, равным М = [2]1/4 = 1,19.
Пример 5.11. Расчет неустойчивого резонатора с зеркалом на выходе, имеющим гауссов профиль коэффициента отражения. Положим у = 0,5, исходя из того, что эта величина оптимизирует мощность излучения на выходе из данного лазера (см. главу 7), и рассмотрим случай, когда поперечный профиль пучка на выходе имеет плоскую вершину. Из (5.6.18) получаем М2 = %/2, из (5.6.17) имеем До=1/М2=1/л/2=0,71, а (5.6.12) дает а’2 =0,41 Радиальные профили коэффициента отражения зеркала на выходе и интенсивности излучения внутри и снаружи резонатора показаны на рис. 5.23. Обозначим теперь через а радиус активной среды и будем считать, что она находится непосредственно перед зеркалом 2, а радиальный профиль интенсивности пучка в среде описывается функцией 1т(г). Для того чтобы избежать излишнего виньетирования пучка апертурой активной среды, т. е. чтобы избавиться от обусловленных таким виньетированием ярко выраженных дифракционных колец, можно, например, наложить условие, что11п(а)/11п(0) = 2 • 10-2. Получим при этом а = 0,9и)т, что для данного размера апертуры а определяет величину характерного параметра ют гауссова профиля коэффициента отражения. Например, если положить а = 3,2 мм, то получим, что шт = 3,5 мм. Таким образом, гауссово зеркало должно иметь максимальный коэффициент отражения Д0 = 71%, характерный параметр профиля ьит = 3,5 мм и быть установлено в неустойчивом резонаторе (например, конфокальном) с увеличением за обход, равным М = [2]1/4 = 1,19.
Второй рассматриваемый случай относится к супергауссову профилю коэффициента отражения [17]. Вместо (5.6.9) и (5.6.10) запишем теперь:
Р = р0 ехр(—гп /и;" ), (5.6.19а)
Д = До ехр(-2гл /И&). (5.6.196)
При п > 2 соотношения (5.6.19) описывают супергауссовы профили коэффициентов отражения. Подстановка соотношения (5.6.19а) в (5.6.7) дает при этом
^20 (г) = ы20(0)ехр (-гп/юп), (5.6.20)
Ю = гит(Мп - 1)1/п. (5.6.21)
Снова имеем, что а = Ро/М иу=1-с2=1- (Д0/М 2). Из (5.6.20) получаем
Теперь
1ы(г) = ^т(0)ехр (-2 г-/IV "). (5.6.22)
Радиальные профили, как и2о, так и 1Ьп, описываются супергауссовыми функциями того же порядка п, что и профили коэффициента отражения. С другой стороны, профиль интенсивности выходящего пучка 1ои1 нетрудно получить из выражения 1оШ = /^(г)[1 - Д(г)], при этом он не описывается су - пергауссовой функцией.
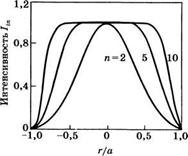
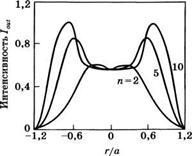 Для того чтобы сравнить работу неустойчивых резонаторов с гауссовым и супергауссовым профилями коэффициента отражения зеркала на выходе, на рис. 5.24а приведены профили интенсивности 1Ы при п = 2 (гауссов профиль) и п = 5, 10 (супергауссовы профили). Кривые нормированы на значения в максимуме, а соответствующие величины характерного параметра и; в выражениях (5.6.22) и (5.6.15) выбраны таким образом, что ехр (-2ап/ьип) = 2 • 10-2, где а — радиус активной среды. Таким образом, сравнение выполнено при одинаковой степени виньетирования пучка активной средой. Основное преимущество супергауссова зеркала по сравнению с гауссовым очевидно из рис. 5.24а: при увеличении порядка п супергауссовы зеркала позволяют более эффективно использовать активную среду (т. е. площадь поперечного сечения моды Ат увеличивается с ростом п). В то же время с ростом п возрастает угол дифракционной расходимости 0^, как это можно понять из рис. 5.246. На нем показаны соответствующие радиальные профили 1оиг(г), рассчитанные при Я0 = 0,45 иМ=1,8. Видно, что по
Для того чтобы сравнить работу неустойчивых резонаторов с гауссовым и супергауссовым профилями коэффициента отражения зеркала на выходе, на рис. 5.24а приведены профили интенсивности 1Ы при п = 2 (гауссов профиль) и п = 5, 10 (супергауссовы профили). Кривые нормированы на значения в максимуме, а соответствующие величины характерного параметра и; в выражениях (5.6.22) и (5.6.15) выбраны таким образом, что ехр (-2ап/ьип) = 2 • 10-2, где а — радиус активной среды. Таким образом, сравнение выполнено при одинаковой степени виньетирования пучка активной средой. Основное преимущество супергауссова зеркала по сравнению с гауссовым очевидно из рис. 5.24а: при увеличении порядка п супергауссовы зеркала позволяют более эффективно использовать активную среду (т. е. площадь поперечного сечения моды Ат увеличивается с ростом п). В то же время с ростом п возрастает угол дифракционной расходимости 0^, как это можно понять из рис. 5.246. На нем показаны соответствующие радиальные профили 1оиг(г), рассчитанные при Я0 = 0,45 иМ=1,8. Видно, что по
|
|
|
А б |
Рис. 5.24
Сравнение гауссова и супергауссовых (п = 5, п = 10) профилей коэффициента отражения зеркала на выходе из неустойчивого резонатора: радиальные профили интенсивности пучка (а) внутри резонатора и (б) на выходе из резонатора (из [18], с разрешения)
Мере возрастания п в поперечном распределении интенсивности пучка на выходе появляется провал увеличивающейся глубины, что приводит к возрастанию расходимости пучка. Следствием этих двух противоположных тенденций является то, что яркость пучка, которую можно считать пропорциональной величине Ат /0^, как функция п имеет максимум. Величина п, соответствующая этому максимуму, зависит от коэффициента увеличения за обход М и коэффициента отражения Д0 в центре зеркала, но во всех практически интересных случаях она изменяется в пределах от 5 до 8 [18]. Таким образом, с точки зрения получения наибольшей яркости пучка, зеркала с супергауссовыми профилями коэффициента отражения порядков п = 5 8
Являются оптимальными для неустойчивого резонатора с зеркалом с переменным коэффициентом отражения.