НАПРАВЛЕННОСТЬ
Это свойство является простым следствием того, что активную среду помещают в резонатор. Например, в случае плоскопараллельного резонатора, изображенного на рис. 1.3, только волны, распространяющиеся в направлении, перпендикулярном к плоскостям зеркал (или очень близком к нему), будут оставаться в резонаторе. Для более глубокого понимания свойств направленности лазерного излучения (или, в общем случае, произвольной электромагнитной волны) удобно отдельно рассмотреть случаи волн с полной и частичной пространственной когерентностью.
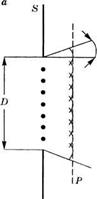 Рассмотрим вначале волну с полной пространственной когерентностью. Даже в этом случае пучок с конечной апертурой будет неизбежно расходиться вследствие дифракции. Эту ситуацию можно представить себе с помощью рис. 1.7, на котором изображена волна с однородным поперечным распределением интенсивности и плоским волновым фронтом, падающая на экран 5 с круговым отверстием диаметром I). Согласно принципу Гюйгенса волновой фронт пучка в некоторой плоскости Р за экраном можно представить как результат суперпозиции элементарных волн (вэйвлетов), испущенных из каждой точки отверстия. Видно, что из-за конечности диаметра отверстия В пучок должен иметь конечную расходимость. Для того чтобы определить
Рассмотрим вначале волну с полной пространственной когерентностью. Даже в этом случае пучок с конечной апертурой будет неизбежно расходиться вследствие дифракции. Эту ситуацию можно представить себе с помощью рис. 1.7, на котором изображена волна с однородным поперечным распределением интенсивности и плоским волновым фронтом, падающая на экран 5 с круговым отверстием диаметром I). Согласно принципу Гюйгенса волновой фронт пучка в некоторой плоскости Р за экраном можно представить как результат суперпозиции элементарных волн (вэйвлетов), испущенных из каждой точки отверстия. Видно, что из-за конечности диаметра отверстия В пучок должен иметь конечную расходимость. Для того чтобы определить
|
|
|
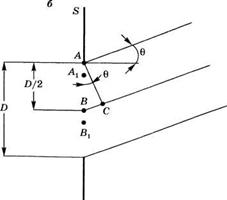
Рис. 1.7 Физическое объяснение расходимости плоской, пространственно-когерентной, электромагнитной волны вследствие дифракции (а) на экране 8 с круговым отверстием диаметра /), (б) на экране 5 с бесконечно длинной щелью шириной В |
Величину угла дифракции Qd, рассмотрим вначале более простой случай, показанный на рис. 1.76, где отверстие представляет собой щель, с шириной D в плоскости рисунка и бесконечной длиной в направлении, перпендикулярном к этой плоскости. Предположим также, что щель равномерно освещена. Из рисунка нетрудно заметить, что интерференция элементарных волн, испущенных из точек в плоскости щели, приводит к нулевой интенсивности в направлении, определяемом таким углом 0, для которого выполняется условие kl = л. Здесь к — это постоянная распространения волны в пространстве, связанная с длиной волны излучения X соотношением к = 2тс/Х, &1 — длина отрезка ВС. Действительно, в этом случае вклады в волну в направлении 0 от вэйвлетов, испущенных из точек А и В, будут противоположны по фазе и, таким образом, будут гасить друг друга. То же самое будет происходить с вэйвлетами, испущенными из точек АЛ и Вх на рисунке, и т. д. Поскольку
I = (D/2)sin0 = (D/2)0, то, полагая, что угол дифракции пучка 0^ равен углу 0, из соотношения kl = n сразу получаем, что dd = X/D.
В более сложных случаях величину угла 0^ можно рассчитать из теории дифракции, если заданы форма отверстия и поперечное распределение интенсивности волны. Обычно получают соотношение
0d = PVD, (1.4.1)
Где множитель Р — это числовой коэффициент порядка единицы, точное значение которого зависит от формы отверстия и вида распределения интенсивности излучения в его плоскости. Действительно, было показано, что в рассмотренном выше случае бесконечной щели р = 1. В качестве других примеров уместно упомянуть, что, как будет видно из последующих глав, Р = 1,22 в случае равномерно освещенного кругового отверстия, тогда как Р = 2/я для пучка неограниченного поперечного размера с гауссовым поперечным распределением интенсивности. Пучок, угол расходимости которого может быть выражен соотношением (1.4.1), в котором р= 1, называют дифракционноограниченным.
Если пучок имеет только частичную пространственную когерентность, то его расходимость будет больше минимальной величины, обусловленной дифракцией. Действительно, для любой точки Р' волнового фронта принцип Гюйгенса (рис. 1.7) может быть применен только к точкам, лежащим в пределах площади когерентности Sc вблизи Р'. Таким образом, размеры области когерентности играют роль ограничивающего отверстия для когерентной суперпозиции элементарных волн. В соответствии с соотношением (1.4.1) угол расходимости пучка можно при этом записать в виде
0 = Pty[SJ1'2, (1.4.2)
Где, как и прежде, р — числовой коэффициент порядка единицы, точное значение которого зависит от того, каким образом определяются как угол расходимости 0, так и площадь когерентности Sc.
Теперь можно показать, что поскольку волны, испущенные из каждой области когерентности, некоррелированы, т. е. некогерентны, друг с другом, на достаточно больших расстояниях (в так называемой дальней зоне)
Рис. 1.8
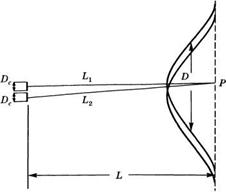 Поперечные профили пучков излучения от двух пространственнонекогерентных источников с диаметром поперечного сечения Dc на большом расстоянии L от источников
Поперечные профили пучков излучения от двух пространственнонекогерентных источников с диаметром поперечного сечения Dc на большом расстоянии L от источников
Необходимо суммировать не напряженности, а интенсивности полей. Для того чтобы обсудить это обстоятельство, обратимся к простой ситуации, изображенной на рис. 1.8, в которой предполагается, что волна представляет собой два когерентных пучка от соседствующих источников, с диаметром поперечного сечения Dc каждый, причем эти пучки абсолютно не когерентны друг с другом. Для большей определенности положим Dc = 100 мкм и X = 1 мкм. В соответствии с соотношением (1.4.1) имеем 0d = 10“2 рад, так что на расстоянии, например, L = 100 м диаметр поперечного сечения пучка, исходящего из первой области когерентности, будет равен D = DC + 2ddL = 2QdL = 2 м. В той же плоскости диаметр поперечного сечения пучка, исходящего из второй области когерентности, будет также равен D, при этом сечения будут сдвинуты на пренебрежимо малую величину, равную Dc. Мгновенное значение интенсивности электромагнитного поля в произвольной точке Р рассматриваемой плоскости может быть представлено как /(Р)а[(Ех(^) 4- E2(t)]2, где Et(t) и E2(t) — напряженности электрических полей, наведенных в точке Р двумя областями когерентности. Полагая, что амплитуды полей постоянны во времени, перепишем это выражение в виде
I(P) = C[Ј10sin (cot 4- фх) 4- Ј20sin (cot 4- ф2)]2,
Где С — некоторая константа, Е10 и Е20 — амплитуды напряженности электрических полей, а фх = фх(£) и ф2 = ф2(0 — соответствующие фазы (см., например, рис. 1.6). Интенсивность, измеряемая любым реальным детектором, будет определяться величиной (/(Р)), которая представляет собой усредненную за несколько периодов колебаний интенсивность 1(Р). Тогда получаем, что эта средняя величина равна
(I(P)) = С[Е?0 (sin2 (cot + ф1)) + Јf0(sin2(cof+ф2)> +
+2Ј10Ј20(sin(cot + фх )sin(cot + ф2))] =
= C[(Ef0 /2) + (Е20 /2) + Е10Е20 (сов(ф2 - фх))].
Заметим, что два фазовых члена, фх(^) и ф2(£), могут быть представлены соответственно в виде фх(£) = vjfx(t) 4- kLx и ф2(£) = j/2(t) 4- kb2, где v*/x и |/2 — фазы напряженностей в рассматриваемых областях когерентности, аЬги Ь2 — рас
стояния от этих областей до точки Р. Поскольку, однако, напряженности электрического поля в двух областях когерентности некоррелированы, то фазы и vj/2(t) также некоррелированы. Таким образом, разность фаз, Фг(0 ~ будет величиной, случайно изменяющейся во времени, так что среднее значение (cos (ф2 - фх)), стоящее в полученном выражении, будет равно нулю. При этом получаем:
<7(Р)> = С[(Я?0 /2) + (Я|0 /2)], т. </(Р)> = 1г + /2,
Где =С(Е120/2)и/2 =С(Е|0/ 2)— соответственно интенсивности электромагнитных волн, пришедших в точку Р из двух областей когерентности.
Согласно приведенному рассмотрению, в любой точке необходимо суммировать интенсивности излучений, полученных из двух областей когерентности. Отсюда следует, что на больших расстояниях суммарный пучок будет иметь такие же поперечные размеры, что и пучок, приходящий из одной зоны когерентности.
Таким образом, имеем: D = 20dL = 2fi(k/Dc)L. Следовательно, угол расходимости пучка составляет 0 = Z)/2L = (3(k/Dc), т. е. равен величине (1.4.2), если считать диаметр Dc равным квадратному корню из площади когерентности Sc.
В заключение общего описания свойств направленности электромагнитных волн следует указать, что при обеспечении определенных условий работы лазера выходящий из него пучок можно сделать полностью пространственно когерентным и, следовательно, дифракционно-ограниченным.