ПРИНЦИПЫ ЛАЗЕРОВ

МОДЕЛЬ ГЕНЕРАЦИИ ВЫСОКИХ ГАРМОНИК НА ОСНОВЕ ТРЕХ СТАДИЙ ВОЗВРАТНОГО СТОЛКНОВЕНИЯ

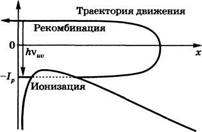
Невозмущенные физические процессы, вызывающие генерацию гармо­ник, могут быть поняты в рамках полу классической модели, включающей три стадии, как показано на рис. 12.19. Когда интенсивность лазера лежит в области между 1013 и 1014 Вт/см2, напряженность электрического поля в ла­зерной волне становится сравнимой с той, которую испытывают электроны внешней оболочки нейтрального атома. В этом случае внешнее поле сильно деформирует кулоновский потенциал атома, что приводит к образованию барьера. Поэтому наиболее слабо связанный электрон может туннелировать через этот барьер и отрываться от атома. Этот процесс не имеет классической аналогии, а является процессом квантовой туннельной ионизации. Затем этот электрон ускоряется лазерным электрическим полем. В зависимости от момента ионизации он может либо отлетать от родительского иона, либо мо­жет ускоряться по направлению к нему. В частности, если электрон оторвался

До пика поля в волне, он никогда не вернется к атомному ядру. Если элек­трон становится свободным в момент максимума электрического поля, он воз­вращается к своему родительскому иону с нулевой кинетической энергией. Если электрон отрывается после максимума поля, он возвратиться к атомному ядру с ненулевой кинетической энергией. Когда электрон встречается с ро­дительским ионом, он может рекомбинировать, образуя атом в своем основ­ном состоянии и испуская фотон с энегией hv = Ip + Ek, где 1р — потенциал ионизации нейтрального атома, а Ek — кинетическая энергия, приобретен­ная электроном в континууме между состояниями ионизации и рекомбина­ции. Можно показать, что максимальная энергия фотона характерна для тех электронов, которые вырываются спустя -0,05 оптического периода после пика приложенного электрического поля и которые сталкиваются с родительским ионом спустя примерно три четверти оптического периода. Эта энергия опре­деляется как hvrnax. = 1р + 3,17 Up, где Up — пондеромоторная энергия, т. е. ус­редненная за период кинетическая энергия колебаний электрона в лазерном поле. Можно показать, что Up - е2Е2 /4тс)§ се где Е — напряженность действующего на электрон лазерного поля, т — масса электрона, ш0иХ0 — угловая частота и длина волны лазерного излучения. Такой трехстадийный процесс периодически повторяется на каждом полупериоде лазерной волны с периодическим испусканием очень короткой вспышки излучения длитель­ностью в аттосекундном диапазоне.

В 1994 г. Левенштейн (Lewenstein et al.) представил более точное физиче­ское описание поведения одиночного атома. При рассмотрении одиночного атома в классическом электромагнитном поле, уравнение Шрёдингера мож­но решить, используя следующие приближения:

■ приближение одиночного активного электрона, т. е. атом рассматрива­ется как водородноподобная система и не учитывается многократная ионизация;

■ приближение сильного поля (SFA): электрон в континууме рассматрива­ется как свободная частица, движущаяся в электрическом поле, т. е. пол­ностью пренебрегается влиянием кулоновского потенциала;

■ рассматривается только основное состояние и континуум, влиянием дру­гих связанных состояний атома пренебрегают.

Используя эти допущения, можно получить простое выражение для ди - польного момента атома, который и является источником испускания гар­моник.

В духе феймановских диаграмм этот дипольный момент можно записать как когерентную суперпозицию лишь нескольких линий (квантовых путей) электрона в диаграмме, которые являются комплексными траекториями, которым следуют электроны от момента ионизации до рекомбинации с роди­тельским ионом. Для того чтобы описать свойства процесса генерации гар­моник, требуется малое число линий в диаграмме. В частности, два вида кван­товых путей дают наиболее существенный вклад: это так называемые корот­кая и длинная траектории, характеризуемые временами движения электрона в континууме т, величины которых составляют соответственно порядка по­ловины и целого оптического периода. Полуклассическая модель и недавние экспериментальные результаты показывают, что в широком спектральном диапазоне время испускания изменяется квазилинейно с повышением по­рядка гармоники, вызывая тем самым неизбежный чирп (называемый атто - чирпом), который является прямым следствием временного уширения вол­нового пакета электрона, совершающего возвратное столкновение. В случае короткого пути этот атто-чирп положительный, т. е. гармоника более высо­кого порядка испускается позже по отношению к низкому порядку, в то время как в случае длинного пути атто-чирп отрицателен. Этот чирп сильно влияет на длительность испускаемых ВУФ-импульсов.