ЛАЗЕРЫ НА СВОБОДНЫХ ЭЛЕКТРОНАХ
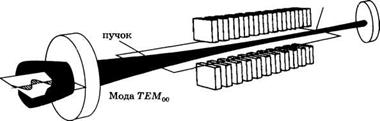
В лазере на свободных электронах (ЛСЭ) [20] электронный пучок, двигающийся со скоростью, близкой к скорости света, пропускается через магнитное поле, создаваемое периодической структурой (называемой виггле - ром или ондулятором) (см. рис. 10.24). Процесс вынужденного излучения происходит за счет взаимодействия электромагнитного поля лазерного пучка с релятивистскими электронами, движущимися в периодической магнитной структуре. Как и в любом другом лазере, для обеспечения обратной связи используются два концевых зеркала. Электронный пучок инжектируется в лазерный резонатор, а затем отклоняется соответствующим изогнутым магнитом.
|
Входной Линейка постоянных электронный магнитов пучок |
![]()
|
Выходной Электронный |
![]()
|
Зеркало |
![]()
|
Выходной пучок |
![]()
|
Выходное Зеркало |
![]()
|
Рис. 10.24 Принципиальная конструкция лазера на свободных электронах (с любезного разрешения Льюиса Элиаса, Калифорнийский университет, Квантовый институт в Санта-Барбаре) |
![]()
|
Плоскость поляризации |
![]() Чтобы понять, как возникает данное взаимодействие, сначала рассмотрим случай спонтанного излучения, т. е. случай, когда зеркала отсутствуют. Будучи инжектированными вдоль периодической структуры, электроны двигаются в плоскости, перпендикулярной магнитному полю, по траекториям, имеющим волнистый вид с завитушками (виггли) (рис. 10.24). Возникающее при этом ускорение электронов приводит к излучению синхротронного типа в продольном направлении. Частоту излучения можно найти эвристически, заметив, что электрон колеблется в поперечном направлении с угловой
Чтобы понять, как возникает данное взаимодействие, сначала рассмотрим случай спонтанного излучения, т. е. случай, когда зеркала отсутствуют. Будучи инжектированными вдоль периодической структуры, электроны двигаются в плоскости, перпендикулярной магнитному полю, по траекториям, имеющим волнистый вид с завитушками (виггли) (рис. 10.24). Возникающее при этом ускорение электронов приводит к излучению синхротронного типа в продольном направлении. Частоту излучения можно найти эвристически, заметив, что электрон колеблется в поперечном направлении с угловой
частотой (од = (2п/Хд)иг = (2лД9)с, где — период магнитов и и2 — средняя продольная скорость электрона (которая практически равна скорости света в вакууме с). Рассмотрим теперь систему координат, которая движется в продольном направлении со скоростью иъ. В этой системе координат электрон совершает колебательное движение по существу в поперечном направлении и поэтому выглядит как колеблющийся электрический диполь. Вследствие лоренцева сокращения времени, частота колебания в рассматриваемой системе координат задается выражением
“, = П, 7,211/2 (10.4.1)
|_1-(иг/с)2]
И таким образом определяет частоту излучения. Если теперь возвратиться в лабораторную систему отсчета, то пучок должен испытывать (релятивистский) доплеровский сдвиг, так что наблюдаемая частота со0 определяется как
|
1-(1’г/С)2 |
|
1/2 |
|
+(уг/с) 1-(1’г/с). |
|
Со0 = |
|
2со, |
|
'і___ , (10.4.2) |
А соответствующая длина волны определяется выражением
^о=^-[1 -(иг/с)2]. (10.4.3)
Заметим, что Х0 может быть намного короче периода магнита, поскольку иг = с. Чтобы вычислить возникающую в выражениях (10.4.2) и (10.4.3) величину [1 - (иг/с)2], заметим вначале, что для абсолютно свободного электрона, движущегося со скоростью иг вдоль оси г, имело бы место следующее равенство: [1 - (иг/с)2] = (т0с2/Е)2, где т0 — масса покоя электрона, а Е — его энергия. Однако при данной энергии траектория в виде вигглей приво* дит к уменьшению значения и2, т. е. множитель [1 - (иг/с)2] увеличивается, Действительно, более подробное вычисление показывает, что эта величина задается выражением
Где числовая постоянная К обычно меньше 1 и называется параметром ондулятора. Она равна К = е(В2)1/2Хд/2пт0с2 (здесь В — магнитное поле ондулятора, а усреднение производится по продольному направлению). Из формул
(10.4.2) и (10.4.3) с помощью (10.4.4) получаем окончательный результат:
Отсюда следует, что длину волны излучения можно перестраивать, изменяя период магнита Хд и/или энергию Е электронного пучка. Выбирая, например, Хд = 10 см и К = 1, находим, что при изменении энергии электронов
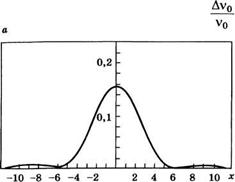
от 102 до 103 МэВ излучаемый свет попадает в диапазон от инфракрасного до ультрафиолетового. Заметим, что, согласно приведенному рассуждению, излучение должно быть поляризовано в плоскости, ортогональной направлению магнитного поля (см. также рис. 10.24). Чтобы найти форму и ширину спектра излучения, заметим, что в рассмотренной выше системе отсчета электрон излучает в течение времени At' = (l/c)[ 1 - (vz/c)2]x/2, где I — полная длина магнита ондулятора. Из выражения (10.4.1) следует, что излучение, испускаемое каждым электроном, имеет вид прямоугольного импульса, содержащего число циклов Ncyc = со'А£'/2я = l/Xq> т. е. равное числу периодов Nw = lfkq ондулятора. Тогда из теории преобразования Фурье следует, что спектр мощности такого импульса имеет вид [sin (х/2)/(х/2)]2, где х = 2nNJy - v0)/v0. При этом полная ширина Av0 (на половине максимального значения) приближенно описывается соотношением
|
2Nir |
![]() (10.4.7)
(10.4.7)
|
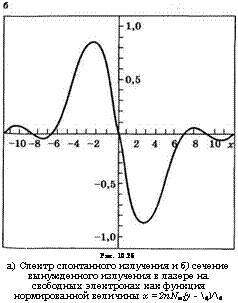
Рис. 10.25 А) Спектр спонтанного излучения и б) сечение вынужденного излучения в лазере на свободных электронах как функция нормированной величины х = 2nNw{y - )/ |
 На рис. 10.25а приведен указанный спектр как функция безразмерной величины х. Поскольку для всех электронов, если их инжектировать с одинаковой скоростью и в одном и том же направлении, будет наблюдаться одна и та же форма линии, то полученная функция соответствует однородному контуру лазера на свободных электронах. Неоднородные эффекты связаны с такими факторами, как разброс энергии электронов, угловая расходимость электронного пучка и неоднородное распределение магнитного поля по сечению пучка. Заметим, что поскольку число периодов ондулятора составляет величину порядка ~ 102, из выражения (10.4.7) получаем Ау0/у0 = 5 • 10 3. Заметим также, что существует и альтернативный способ описания свойств испускаемого излучения. В движущейся вместе с электроном системе отсчета, которая была рассмотрена выше, магнитное поле ондулятора будет двигаться со скоростью, близкой к скорости света. Можно показать, что в этом случае статическое магнитное поле будет выглядеть для
На рис. 10.25а приведен указанный спектр как функция безразмерной величины х. Поскольку для всех электронов, если их инжектировать с одинаковой скоростью и в одном и том же направлении, будет наблюдаться одна и та же форма линии, то полученная функция соответствует однородному контуру лазера на свободных электронах. Неоднородные эффекты связаны с такими факторами, как разброс энергии электронов, угловая расходимость электронного пучка и неоднородное распределение магнитного поля по сечению пучка. Заметим, что поскольку число периодов ондулятора составляет величину порядка ~ 102, из выражения (10.4.7) получаем Ау0/у0 = 5 • 10 3. Заметим также, что существует и альтернативный способ описания свойств испускаемого излучения. В движущейся вместе с электроном системе отсчета, которая была рассмотрена выше, магнитное поле ондулятора будет двигаться со скоростью, близкой к скорости света. Можно показать, что в этом случае статическое магнитное поле будет выглядеть для
Электрона как набегающая электромагнитная волна. Поэтому можно считать, что синхротронное излучение обусловлено комптоновским рассеянием назад этой «виртуальной» электромагнитной волны на электронном пучке. По этой причине соответствующий тип ЛСЭ иногда называют работающим в комптоновском режиме (комптоновский ЛСЭ).
Чтобы вычислить сечение вынужденного излучения, необходимо провести подробный анализ взаимодействия распространяющейся в продольном направлении электромагнитной волны с электроном в знакопеременном магнитном поле. Мы не будем рассматривать здесь этот анализ, но укажем лишь на то, что в отличие от всех рассмотренных до сих пор лазеров спектральное распределение этого сечения не совпадает со спектром спонтанного излучения, а пропорционально его производной по частоте. Форма спектра сечения вынужденного излучения приведена на рис. 10.256. Таким образом, видно, что со стороны низких частот перехода имеет место усиление, а со стороны высоких — ослабление. Такое необычное поведение является результатом того, что взаимодействие основано на процессе рассеяния света, а не поглощения или излучения из связанных состояний.
К настоящему времени во многих лабораториях мира продемонстрирована работа ЛСЭ на нескольких установках (более 10), причем длины волн генерации лежат в диапазоне от миллиметровых волн вплоть до ультрафиолетовой области спектра. На различных этапах разработки сейчас находится значительно большее число таких лазеров. Все они требуют установок весьма больших размеров, поскольку для их работы необходимо использовать довольно большие ускорители электронных пучков. Исторически самый первый ЛСЭ был запущен на длине волны X = 3,4 мкм с помощью линейного сверхпроводящего ускорителя в Станфордском университете в США [21]. Поскольку входной электронный пучок имел вид импульсов длительностью 3,2 пс, разделенных промежутками т = 84,7 не, длина резонатора Ь выбиралась так, чтобы величина фбыла равна времени полного прохода резонатора (т. е. Ь = ст/2 = 12,7 м). Таким образом, лазер работал в режиме синхронизации мод с синхронной накачкой. Один из наиболее важных моментов для ЛСЭ связан с эффективностью этих лазеров. Поскольку частота генерируемого ими излучения зависит от энергии электронов (см. выражение (10.4.5)), максимальная энергия, которую можно отвести от электрона, равна такому изменению энергии электрона, при котором соответствующая рабочая частота смещается за пределы контура усиления. Следовательно, максимальный КПД гтах, определяемый как отношение максимальной энергии, отдаваемой лазерному пучку, к начальной энергии электронов, примерно равен именно отношению Ау0/у0, т. е. Цтах = (1/2А/ы,). Отсюда следует, что КПД такого устройства весьма мал (10'2 - 10“3). В настоящее время активно ведутся работы с целью повышения КПД по двум направлениям:
■ с целью сохранения постоянным отношения /Е2 постепенно уменьшают период магнита вдоль электронного пучка (спадающий вигглер);
■ энергия, оставшаяся в электронном пучке после того, как он вышел из ондулятора, возвращается обратно за счет замедления электронов.
Предполагается, что, используя эти методы, можно добиться значительно более высоких КПД, что и было в некоторой степени достигнуто.
В качестве заключительного комментария следует указать на то, что рассмотренные до сих пор ЛСЭ используют ускорители электронных пучков высокой энергии (Е > 10 МэВ), но небольших токов (/ - 1-100 А). При этих условиях, как уже упоминалось выше, излучение света можно рассматривать как комптоновское рассеяние виртуальных квантов магнитного поля на отдельных электронах (комптоновскийрежим ЛСЭ). Были запущены также ЛСЭ, использующие электронные пучки низкой энергии (Е = 1-2 МэВ) со значительно большими токами (/ ~ 10-20 кА). В этом случае электрон- электронное взаимодействие становится столь сильным, что в электронном пучке во время взаимодействия с электромагнитной волной в ондуляторе возбуждаются коллективные колебательные движения (плазменные волны), и излучение теперь возникает вследствие рассеяния виртуальных квантов магнитного поля на этих коллективных движениях, а не на отдельных электронах. При этом частота излучения у0 = 2я/со0 Уже задается выражением (10.4.5), а фактически сдвигается в низкочастотную область на величину, определяемую этим коллективным движением. Это явление аналогично комбинационному (рамановскому) рассеянию света на молекулярных колебаниях, поэтому соответствующий лазер называется ЛСЭ в рамановском режиме. Вследствие более низкой энергии электронов, участвующих в работе лазера, все эти лазеры генерируют в миллиметровом диапазоне.
В заключение данного раздела укажем наиболее привлекательные свойства ЛСЭ: (1) возможность широкой перестройки частот излучения; (2) прекрасное качество пучка, близкое к дифракционному пределу, а в перспективе и (3) очень высокий КПД, следовательно, и очень высокая мощность лазерной генерации (средняя мощность электронного пучка Станфордского линейного ускорителя составляет примерно 200 кВт). Однако ЛСЭ являются принципиально громоздкими и дорогими установками, и, по-видимому, наибольший интерес, с точки зрения применимости, они могут представлять только в той области частот, для которой не имеется традиционных лазеров, например в дальней ИК-области (100-400 мкм) или в области вакуумного ультрафиолета (А, < 100 нм).