ПРИНЦИПЫ ЛАЗЕРОВ

ЛАЗЕРЫ НА ДВОЙНОМ ГЕТЕРОПЕРЕХОДЕ

Ограничения, описанные в предыдущем разделе, сдерживали широкое использование полупроводниковых приборов до тех пор, пока не были пред­ложены вначале лазеры на одинарных гетеропереходах, а вскоре после это­го — лазеры на двойных гетеропереходах (ДГ-лазеры). В данном разделе наше внимание будет обращено лишь на последний тип лазеров, поскольку именно они наиболее широко используются в наши дни.

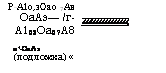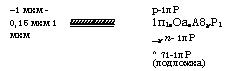Рис. 9.21

Схематическое представление двойной гетероструктуры, в которой активная среда (заштрихованная площадь) состоит из материала ОаАв (а) или ГпОаАэР (6)

На рис. 9.21а и б приведены два примера лазера на двойном гетеропере­ходе, где активная среда представляет собой тонкий слой (0,1-0,2 мкм) ма­териала ОаАэ или четверного сплава ГпОаАвР. Для обоих обсуждаемых слу­чаев р - и п области выполнены из материалов А10 3Оа0>7А8 и 1пР соответствен­но. При оптимизации пороговая плотность тока (см. рис. 9.23) при комнатной температуре в такой диодной структуре может быть уменьшена практически на два порядка (т. е. до 103 А/см2) по сравнению с соответствующими устрой­ствами на гомопереходах, что позволяет без труда осуществить непрерыв­ную лазерную генерацию при комнатной температуре. Значительное умень­шение пороговой плотности тока происходит благодаря совместному дейст­вию трех следующих факторов:

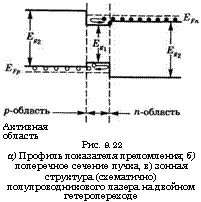
1. Показатель преломления активного слоя щ (например, пг = 3,6 для ОаАв) значительно больше, чем показатель преломления п2 внешних слоев р - и дг-типа (например, п2 = 3,4 для А10>3Оа0>7Ав), что приводит к образова­нию оптической волноводной структуры (см. рис. 9.22а). Это означает, что теперь лазерный пучок будет сосредоточен главным образом в активном слое ОаАв, т. е. в области, в которой имеется усиление (локализация фотонов, см. рис. 9.226).

2. Ширина запрещенной зоны Её1 активной области (например, Её1 «1,5эВ в ОаАв) значительно меньше ширины запрещенной зоны внешних слоев Е6% (например, Её2 = 1,8 эВ для А10 дОа^Ав).[55] Поэтому на обоих переходах обра­зуются энергетические барьеры, которые эффективно удерживают инжек­тированные электроны и дырки в активном слое (локализация носителей, см. рис. 9.22в). Таким образом, для данной плотности тока концентрация

Дырок и электронов в активной области увеличивается, и, как следствие, возрас­тает усиление.

3.

Поскольку Её2 значительно больше, чем Её1, краевые области лазерного пуч­ка с частотой у = Её1/к значительно мень­ше поглощаются во внешних слоях (см. рис. 9.226), и потери в данном случае обу­словлены только свободными носителями (уменьшенное поглощение).

Для создания двойной гетерострук­туры и реализации всех ее преимуществ должно выполняться очень важное требо­вание, а именно: период решетки актив­ного слоя должен совпадать (с точностью до -0,1%) с периодом решетки внешних слоев.[56] Действительно, если это условие не выполняется, результирующее механиче­ское напряжение на двух граничащих по­верхностях будет приводить к возникно­вению нежелательных дефектов решетки (дислокаций). Каждая дислокация дейст­вует как активный центр для электронно­дырочной безызлучательной рекомбина­ции. Для структуры ОаАв/АЮаАз требо­вание согласования решеток не является проблемой, поскольку периоды решеток ОаАв (0,564 нм) и А1Аз (0,566 нм) очень близки по значению (атомные радиусы элементов Оа и А1 практически одинаковы). Для четверного сплава 1п1.хОа. хА^уР1.у и слоя, выполненного из материала 1пР, можно достичь согласования решеток при определенном от­ношении у/х, что проясняет следующая аргументация. Предположим, что изначально в качестве активной области выступает слой 1пР, затем добавля­ется некоторая доля х атомов Оа, замещающих атомы 1п в решетке (число которых с этого момента становится 1п1.л:). Поскольку радиус атома Оа мень­ше (на -19 пм), чем радиус атома 1п, период решетки 1п1.л. Оал;Р уменьшится по сравнению с 1пР. Предположим теперь, что некоторая доля у атомов Ав (Ав^) замещает атомы Р (которых теперь осталось Р^). Поскольку радиус атома Ав больше (на -10 пм), чем радиус атома Р, эта добавка приведет к увеличению периода решетки. Таким образом, при определенном отноше­нии у/х долей двух веществ эти два эффекта будут компенсировать друг дру­га, что приведет к согласованию решеток 1п1.л:ОалА81/Р1.1/ и 1пР. Условие со­гласования решеток для указанных материалов будет выполняться при у ~ 2,2л:. Изменяя параметр х, при постоянном отношении у/х (которое соот­ветствует значению при полном согласовании постоянных решеток), можно

Расчетные (непрерывная и пунктирная линии) и экспериментальные (темные и светлые кружки) значения пороговой плотности тока Jth как функции толщины активной области й для полоскового ДГ АЮаАв лазера с длиной перехода 300 мкм:

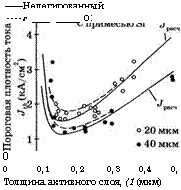Темные и светлые кружки представляют данные для ширины полосок 40 и 20 мкм соответственно. Теоретические кривые относятся к случаям нелегированного и слаболегированного кремнием активных

Слоев. (Согласно работе [41].)

Изменять ширину запрещенной зоны и соответственно длину волны излуче­ния. Таким образом, длина волны излучения в структуре 1Щ-хОа. хАзуРх. у может изменяться в диапазоне 1150-1670 нм в случае непрерывной генера­ции при комнатной температуре. Указанный диапазон длин волн попадает в так называемое второе (-1300 нм) и третье (-1500 нм) окна прозрачности кремниевых оптических волокон.

На рис. 9.23 показаны экспериментальная и теоретическая зависимости пороговой плотности тока от толщины активной области й для полоско­вого ДГ ОаАв лазера [41]. Отметим, что при уменьшении толщины <2 порого­вая плотность тока «7^ сначала уменьшается, затем достигает минимального значения (е/*л = 1 кА/см2 при <2 = 0,1 мкм) и после этого увеличивается. Что­бы понять такой характер поведения, необходимо сначала связать пороге^ вую плотность тока с пороговой концентрацией носителей Обозна* чим вначале через Шр скорость, с которой электроны (и дырки) инжектируй ются в единицу объема активной области. Положим также, что величина которая обычно характеризует внутреннюю квантовую эффективность, в дан­ном случае является долей носителей зарядов, которые излучательно реком­бинируют в этом слое; при этом оставшаяся часть претерпевает безызлуча - тельную электронно-дырочную рекомбинацию (по большей части на грани­цах перехода). Число г]1 также можно рассматривать как эффективную долю инжектированных носителей, в то время как всю оставшуюся часть можно считать долей, не инжектированной в активную область. Тогда для заданной плотности тока <3, протекающего через переход, скорость Яр можно принять равной Яр = т)^е//ей, где е — заряд электрона и (2 — толщина активной облас­ти. В стационарном режиме простое условие баланса дает соответствующее выражение для концентрации носителей N = Яртг, где тг — время излуча - тельной рекомбинации (в предположении, как уже оговаривалось ранее, что все носители зарядов излучательно рекомбинируют в активной области). Из двух предыдущих выражений можно получить соотношение J = edN/riтr, так что вблизи порога генерации имеем:

(9.4.3)

С помощью выражения (9.4.3) можно качественно объяснить поведение зависимостей, приведенных на рис. 9.23. Во-первых, следует отметить, что при достаточно больших значениях й пороговая концентрация носителей ЫгН оказывается практически равной концентрации прозрачности Ыгг (см. при­мер 9.1) и, таким образом, является константой. Из выражения (9.4.3) так­же видно, что при больших значениях (1 (больших, чем ~0,15 мкм) зависи­мость Jth отй носит линейный характер, что собственно и наблюдается на рис. 9.23. Тем не менее, когда толщина й становится очень малой, поле уже не удерживается внутри активного слоя (см. рис. 9.226), и крылья пучка будут проникать в р - и л-области перехода, претерпевая существенные поте­ри. Такая ситуация приведет к уменьшению эффективного усиления и в то же время к увеличению потерь, возникающих во внешнем слое, и оба эти эффекта приведут к существенному увеличению Таким образом, при дос­

Таточно малых значениях й пороговый ток Jth будет возрастать с уменьше­нием толщины <1.

Пример 9.1. Пороговая плотность тока и пороговая концентрация носителей для ДГ-СаЛэ лазера. Поскольку лазерное поле является про­странственно зависимым, пороговое условие должно записываться (как и в предыдущих примерах, см. раздел 6.3.4) исходя из условия, что простран­ственно-усредненное усиление должно быть равно пространственно-усред­ненным потерям. Таким образом, в этом случае имеем:

(В)Ь = (а а)Ь + (а п)Ь + <ар)Ь + уж, (9.4.4)

Где Ь — длина активной среды, £ — коэффициент усиления, аа — потери на рассеяние в активном слое, ап и ар — потери вп-и р-областях соответст­венно и ут — потери на зеркалах. Средние значения в выражении (9.4.4) вычисляются по распределению интенсивности поля. Так что среднее уси­ление, например, можно описать следующим образом:

^и? аг

(9-4-5>

С

Где Щх, у, г) — распределение поля внутри лазерного резонатора. При этом интеграл в числителе берется по объему активной среды, а интеграл в зна­менателе берется по всему объему резонатора. Величины (#) и (ё)Ь обычно называются модальным коэффициентом усиления и модальным усилени­ем соответственно. Подобные выражения имеют место и для средних зна­чений, приведенных в правой части формулы (9.4.4). При этом, как уже говорилось, интеграл в числителе всегда берется по объему активной сре­ды рассматриваемого вещества. Для простоты предположим, что ап = ар = а. Пренебрегая пространственными изменениями напряженности поля в ре­зонаторе вдоль продольной координаты ъ (как, например, в случае стоячей волны) и вдоль координаты, параллельнойр-гс-переходу, с помощью соот­ношения (6.4.5) и соответствующих выражений для (аа) и (ар) из (9.4.4) находим:

£Г = ааГ + а(1 — Г) + [1п(1/Д)/£], (9.4.6)

Где Я — коэффициент отражения двух торцевых зеркал (предполагается одинаковым для обоих зеркал) и

+а/2

І иг сіх

(9.4.7)

Где х — координата вдоль направления, перпендикулярного переходу. Ве­личина Г представляет собой долю мощности пучка, которая находится в активном слое и обычно называется фактором локализации пучка (или фак­тором оптического ограничения). Согласно рассуждениям, приведенным в разделе 3.2.5, можно аппроксимировать функцию # следующим образом: ё = сг(ІУ - А/^), где а — дифференциальный коэффициент усиления и А/,г — концентрация прозрачности носителей. Если теперь положить для просто­ты, что аа = а, то выражение (9.4.6) можно упрощенно записать в виде:

АГ(ЛГ,„ - Ы1Г) = а + [1п (1 /Щ/Ь = у/Ь,

Где — пороговая концентрация носителей и у = аЬ + 1п (1/К) — полные потери за проход. Из выражения (9.4.8) окончательно получаем искомое соотношение для пороговой концентрации носителей:

Ыт = (у/аЬГ) + М1г.

Теперь, чтобы продолжить вычисления, необходимо определить фак­тор локализации пучка Г, который задается довольно точным и простым выражением [42]:

Г = Б2/(2 + Б2),

Где величина

£> = 2я(л?-п|)1/2с! Л

Является нормированной толщиной активного слоя (как уже отмечалось, пх и п2 — показатели преломления активной среды и внешних слоев соот­ветственно). Теперь, если принять пг = 3,6, п2 = 3,4 и X = 850 нм (что свой­ственно для ОаАэ лазера) и провести вычисления для (I = 0,1 мкм, то по­лучим £> = 0,875 и отсюда Г = 0,28. Чтобы оценить соответствующее зна­чение будем считать коэффициент отражения двух торцов кристалла

Равным отражению непокрытых поверхностей (т. е. Л = 32%) и выберем коэффициент потерь равным а = 10 см1 и длину резонатора равной Ь = = 300 мкм. В итоге получаем у = 1п(1/Я) + аЬ = 1,44. Если теперь принять (см. табл. 3.1) а = 3,6 ■ 10~16 см2 и Л^г = 2 ■ 1018 см-3, то из выражения (9.4.9) находим:

= (0,48 + 2) х 1018 носителей/см3,

Где для удобства численные значения двух членов в правой части выраже­ния (9.4.9) показаны отдельно. Таким образом, из выражения (9.4.12) вид­но, что в данном случае для достаточно больших значений и, следова­тельно, фактора локализации пучка Г первый член (т. е. концентрация но­сителей, необходимая для преодоления потерь в резонаторе) является относительно малой долей от величины Л^г.

Пороговая плотность тока теперь легко находится при подстановке выражения (9.4.9) в (9.4.3):

(9.4.13)

Как уже было показано, для достаточно больших значений <2 концен­трация Л^г является преобладающим членом в квадратных скобках выра­жения (9.4.13). И в этом случае можно ожидать, что величина*/^ будет пропорциональна толщине <2, что в действительности и отображено на рис. 9.23 для больших значений д (больше, чем -0,15 мкм). При этом зна­чительная часть порогового тока накачки используется только для того, чтобы достигнуть условия прозрачности полупроводника. Тем не менее, когда толщина (1 становится очень малой, фактор локализации пучка так­же уменьшается (согласно выражению (9.4.10), для очень малых значе­ний (I имеем Г ос с?2)). Тогда первый член в скобках, в конечном счете, будет преобладать, и величина Jth достигнет точки, после которой она станет снова возрастать с уменьшением й. Чтобы получить численное значение Jth из выражения (9.4.13), положим <2 = 0,1 мкм, г|* = 1 и тг = 4 не и используем предварительно вычисленное значение (см. выше). В этом случае полу­

Чаем пороговую плотность тока = 103 А/см2, что достаточно хорошо со­гласуется с графиками, приведенными на рис. 9.23.