ПРИНЦИПЫ ЛАЗЕРОВ

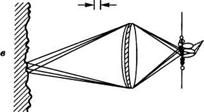
ЛАЗЕРНАЯ СПЕКЛ-КАРТИНА

После рассмотрения вопроса о когерентности первого порядка, приве­денного в разделе 11.3, следует упомянуть об удивительном явлении, харак­терном для лазерного излучения и называемом спекл-картиной [8, 9]. Спекл - картину можно увидеть, если наблюдать лазерный свет, рассеянный от сте­ны или рассеивающего транспаранта. Наблюдаемый рассеянный свет состоит из скопления ярких и темных пятен (или спек лов), см. рис. 11.8а. Несмотря на хаотическое распределение пятен можно различить пятно (или зерно) сред­них размеров. Из первых же работ и публикаций по данной теме стало ясно, что это явление обусловлено интерференцией вторичных волн с усилением и ослаблением, распространяющихся от небольших рассеивающих центров, расположенных на поверхности стены или рассеивающего транспаранта. Поскольку рассматриваемое явление наблюдается только тогда, когда излу­чение имеет высокую степень когерентности первого порядка, оно представ­ляет собой неотъемлемое свойство лазерного излучения.

Физическую природу наблюдаемой зернистости нетрудно понять как при распространении света в свободном пространстве (рис. 11.86), так и при рас-

Пространении его через систему формирования изображения (рис. 11.8в), если рассмотреть случай, когда рабочие поверхности рассеивателей имеют очень большую шероховатость в масштабе оптических длин волн. При распростра­нении в свободном пространстве результирующая оптическая волна в любой точке, находящейся на не слишком большом расстоянии от рассеивающей поверхности, состоит из многих когерентных компонент или элементарных волн, каждая из которых испускается со своего микроскопического элемен­та поверхности. Обратившись к рис. 11.86, заметим, что расстояния, прой­денные этими различными волнами, могут отличаться на много длин волн. Интерференция сдвинутых по фазе, но когерентных элементарных волн при­водит к зернистому распределению (или спекл-картине, как ее обычно назы­вают). Если оптическое устройство представляет собой систему формирова­ния изображения (рис. 11.8в), то при объяснении наблюдаемой картины необ­ходимо учитывать и дифракцию, и интерференцию. Действительно, вследствие ограниченной разрешающей способности даже самой идеально скорректиро­ванной системы формирования изображения, интенсивность света в данной точке изображения может быть результатом когерентного сложения вкла­дов световых волн, испущенных из многих независимых участков поверхно­сти. Данная ситуация встречается на практике, когда функция рассеяния точки (или функция разрешения) для системы формирования изображения оказывается достаточно широкой по сравнению с микроскопическими де­фектами поверхности.

Нетрудно получить оценку по порядку величины размера зерна йе (т. е. среднего размера пятен в спекл-картине) для двух рассмотренных выше схем. В первом случае (см. рис. 11.9а) рассеянный свет регистрируется на фото­пленке, расположенной на расстоянии Ь от рассеивателя, причем между фо­топленкой и рассеивателем отсутствуют какие-либо оптические элементы (на­пример, линзы). Предположим, что в плоскости регистрации, в некоторой точке Р существует светлый спекл. Это означает, что свет, дифрагированный

Плоскость

Плоскость Регистрации

Рис. 11.9 К расчету размера зерна спекл-картины при распространении света в свободном пространстве (а) и через систему, формирующую изображение (б)

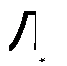На всех точках рассеивателя, будет интерферировать в точке Р преимущест­венно с усилением, давая в результате ненулевое значение амплитуды поля. Подходя эвристически, можно утверждать, что вклады от дифракции в точ­ке Р от волн, рассеянных в точках Рх, Р/иР2 и т. д., складываются (в сред­нем) в фазе с волнами, рассеянными в точках Р2, Р2, Р£ и т. д. Теперь можно задать вопрос: как далеко необходимо переместить точку Р вдоль оси л: в плоскости регистрации, чтобы расстроить наблюдаемую картину интерфе­ренции с усилением? Это произойдет, когда вклады от волн, дифрагиро­ванных, например от точек Рг и Р2 в новую точку Р', будут интерфериро­вать с ослаблением, а не с усилением. В этом случае можно показать, что вклады от точек Р[ и Р2 будут также интерферировать с ослаблением, как и в случае точек Р{иР2 и т. д., и полная интенсивность света будет иметь минимальное значение. Например, выберем точки Рг и Р2 и потребуем, что­бы изменение дх координаты х точки Р было таким, чтобы соответствующее изменение 8(Р2Р - РХР) разности длин Р2Р - РгР было бы равно Х/2. Посколь­ку расстояние Р2Р = (х2 + Ь2)1/2 и расстояние РХР = {[(£>/2) - х]2 + Х,2}1/2, то (для В Ь) получаем 8(Р2Р - РР) = (В/2Ь)дх. Если потребовать выполне­ния равенства 8(Р2Р - РХР) = Х/2, то можно записать:

Дх = ХЬ/В. (11.5.1)

Проведя аналогичные вычисления, нетрудно показать, что точно такой же результат получается, если рассматривать точки Р{иР2 (или точки Р{иР2 и т. д.), а не точки Рг и Р2. Теперь все соответствующие вклады от волн (в сред­нем) будут складываться с ослаблением, а не с усилением. Таким образом, для размера зерна можно записать следующее приближенное выражение:

Йё=2Ьх = 2 ХЬ/В. (11.5.2)

Чтобы получить приближенное выражение для размера зерна в случае применения системы формирования изображения (рис. 11.8б), можно исполь­зовать аналогичный подход, который использовался при расчете диаметра пятна пучка в фокальной плоскости линзы (диска Эйри). Рассмотрим слу­чай, когда рассеиватель на рис. 11.9а помещен перед линзой с фокусным расстоянием f = L. Тогда максимум интенсивности будет располагаться в точ­ке с координатой х = 0 (т. е. в центре плоскости регистрации), поскольку линза даст сферический волновой фронт, и вклады от волн, дифрагирован­
ных в точках Ръ Р{, Р{ и т. д., будут складываться в фазе с волнами, исходя­щими из точек Р2, Р2,Р2 и т. д. Размер пятна в фокальной плоскости снова приближенно дается выражением (11.5.2), и для рассматриваемого случая составляет (1ё=2кЬ/В. Этот результат необходимо сравнить со значением с1ё = 2,44кЬ/В, полученным из функции Эйри, см. рис. 11.6. Из этого приме­ра можно понять следующее общее свойство дифрагированной волны: если вся апертура диаметром В дает когерентный вклад при формировании одного или многих пятен дифрагированным светом в плоскости регистрации, распо­ложенной на расстоянии Ь, то в любом случае минимальный размер пятна в этой плоскости приближенно равен 2кЬ/В.[73] Следует заметить, что в случае рассеивателя этот когерентный вклад от всей апертуры В имеет место при ус­ловии, что: 1) диаметр й8 отдельного рассеивающего центра гораздо меньше диаметра отверстия В и 2) в плоскости регистрации имеется существенное пе­рекрытие между дифрагированными пучками от различных рассеивающих центров. Это означает, что сечение любого из этих пучков в плоскости регист­рации (~кЬ/с18) оказывается больше, чем среднее расстояние между ними (~В). Следовательно, длина Ь должна быть такой, чтобы выполнялось неравенст­во I/ > й8В/к. Например, если с18 = 10 мкм и к = 0,5 мкм, то Ь > 20В.

Теперь рассмотрим случай, когда рассеянный свет регистрируется на фо­топленке после того, как он прошел через линзу, проецирующую изображе­ние рассеивателя на фотопленку (см. рис. 11.96). Предположим, что аперту­ра линзы равна В' и что апертура полностью заполняется светом, дифраги­рующим на отдельных рассеивателях (т. е. (2кЬ/с18) ^ В’). В этом случае вся апертура линзы дает вклад в дифракционную картину на фотографической пластине и размер зерна с1ё на пластине задается выражением:

Аё=2кЬ,/В (11.5.3)

Следует заметить, что устройство на рис. 11.96 также соответствует слу­чаю, когда глаз смотрит непосредственно на рассеивающую поверхность. В этом случае линзой служит хрусталик, а плоскостью регистрации — сетчатка гла­за. Соответственно, величина^, определяемая выражением (11.5.3), пред­ставляет собой диаметр зерна на сетчатке глаза. Следует отметить, что види­мый диаметр (1аё зерна на рассеивающей поверхности определяется как

(1аё = (1ё(Ь/Ь’) = 2 кЬ/В (11.5.4)

Из этого выражения, которое определяет разрешающую способность гла­за для объекта, расположенного на расстоянии Ь, видно, что величина с1аё возрастает с увеличением расстояния Ь, т. е. с увеличением расстояния меж­ду наблюдателем и рассеивающей поверхностью, и уменьшается с увеличе­нием апертуры хрусталика (например, когда глаз адаптирован к темноте). Оба этих результата действительно подтверждаются в экспериментах.

Спекл-шум зачастую является нежелательным свойством когерентно­го света. Пространственное разрешение объектов, освещенных лазерным

Светом, во многих случаях ограничивается спекл-шумом. Спекл-шум возни­кает также в реконструированном изображении голограммы и ограничивает пространственное разрешение этого изображения. Поэтому были разработа­ны методы, которые уменьшают влияние спекл-картины при когерентном освещении объектов [9]. Однако спекл-шум не всегда является вредным эф­фектом. Действительно, разработаны методы, использующие свойства спекл - картины (<спекл-интерферометрия), которые позволяют довольно простым способом определять деформации крупных объектов, вызываемые, напри­мер, напряженностями или вибрациями.

Пример 11.5. Размер зерна спекл-картины, видимой наблюдателем. Рассмотрим пучок красного цвета от He-Ne лазера (длина волны излуче­ния X = 633 нм), освещающий площадь диаметром D = 2 см на рассеиваю­щей поверхности, для которой характерный размер отдельных рассеиваю­щих центров составляет d8 = 50 мкм. Рассеянный свет регистрируется гла­зом человека на расстоянии L = 50 см от рассеивателя. Пусть I/ = 2 см — расстояние между сетчаткой глаза и хрусталиком, и пусть D' = 2 мм — диа­метр зрачка. Поскольку величина (2XL/d8) =12,7 мм существенно больше диаметра!)', то вся апертура зрачка заполняется светом, дифрагирован­ным от каждого отдельного рассеивателя. Видимый размер спекла в осве­щенной области рассеивателя определяется выражением (11.5.4) и состав­ляет dag =316 мкм. Следует отметить, что если наблюдатель переместится на расстояние L = 100 см от рассеивателя, то видимый размер зерна на ос­вещенном пятне (диаметром D = 2 см) рассеивателя будет в два раза боль­ше и составит ~632 мкм.