ПРИНЦИПЫ ЛАЗЕРОВ

КОГЕРЕНТНОСТЬ

В первом приближении, для любой электромагнитной волны можно вве­сти две независимых характеристики когерентности, а именно: простран­ственную когерентность и временную когерентность. Для того чтобы оп­ределить понятие пространственной когерентности, рассмотрим две точки Рг и Р2, выбранные таким образом, что в момент времени t = 0 они находятся
на одном и том же волновом фронте некоторой электромагнитной волны, и пусть Ex(t) и E2(t) — соответствующие напряженности электрического ПОЛЯ в этих точках. По определению, в момент времени t = О разность фаз напря­женностей электрического поля в этих точках равна нулю. Если эта разность фаз остается равной нулю в любой момент времени t > О, то говорят, что между этими двумя точками имеется полная когерентность. Если такая ко­герентность существует между любыми парами точек волнового фронта, то говорят, что данная волна характеризуется полной пространственной коге­рентностью. В реальности, для любой точки Рг все точки Р2> Фаза напря­женности поля в которых достаточно коррелирована с фазой в точке Ри рас­полагаются внутри некоторой конечной области вокруг этой точки Рг. В этом случае говорят, что волна характеризуется частичной пространственной когерентностью, причем для любой точки Р можно определенным образом ввести площадь когерентности SC(P).

Для того чтобы определить понятие временной когерентности, рассмот­рим напряженности электрического поля электромагнитной волны в данной точке Р в моменты времени t и t + т. Если при данной задержке х разность фаз напряженностей поля остается постоянной в любой момент времени t, то говорят о существовании временной когерентности на интервале времени х. Если это условие сохраняется при любом значении х, то говорят, что волна характеризуется полной временной когерентностью. Классически электро­магнитной волной с полной временной когерентностью является такая, на­пряженность электрического (и магнитного) поля которой может быть пред­ставлена синусоидой вида Е = 2Ј0sin (cot + ф), где как амплитуда Е0, так и фа­за ф не зависят от времени. В этом случае разность фаз в моменты времени t и

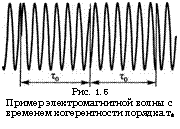T + х, равная Лф = [со(* + х) + ф - (cot 4- ф)] = сох, действительно не зависит от времени. Если же разность фаз напряженностей поля остает­ся постоянной (в среднем) при таких задерж­ках х, что 0 < х < х0, то говорят о частичной временной когерентности волны, с харак­терным временем когерентности х0. Пример электромагнитной волны с временем коге­рентности, равным (примерно) х0, приведен на рис. 1.5. Эта волна представляет собой сину­соидальное электрическое поле со скачкооб­разными изменениями фазы через промежутки времени х0. В этом случае при х < х0 разность фаз напряженностей поля остается постоянной, т. е. рав­ной сох, для всех моментов времени t, кроме тех, для которых в интервале между моментами времени t и t + х происходит скачок фазы. Напротив, если х > х0, то произвольный скачок фазы в интервале между моментами време­ни t и t + х происходит всегда, так что получаемая разность фаз будет случай­ной величиной, изменяющейся в интервале от О до 2л.

Можно заметить, что волна, изображенная на рис. 1.5, не является моно­хроматической. Действительно, если применить к соответствующему сигна­лу преобразование Фурье, то можно показать, что спектральная ширина это­
го сигнала будет составлять Ду = 1/т0. Таким образом, по крайней мере в рас­смотренном случае, время когерентности равно тс = 1 /Ду, а представление о временной когерентности, как видно, напрямую связано с понятием моно­хроматичности. Однако в главе 11 будет показано, что приведенные резуль­таты справедливы для любой стационарной электромагнитной волны. В той же главе покажем, что в случае нестационарного, но периодически повто­ряющегося излучения (например, излучения, получаемого в результате пе­риодической модуляции добротности резонатор^ или синхронизации мод ла­зера), время когерентности не связано обратно пропорциональной зависимо­стью с шириной спектра генерации Ду и фактически может намного превы­шать величину 1/Ду.

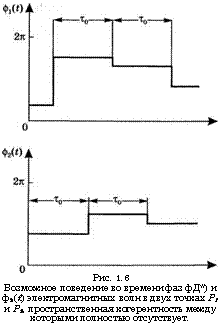Важно отметить, что временная и пространственная когерентности не связаны друг с другом. Действительно, можно привести примеры волн с пол­ной пространственной и только частич­ной временной когерентностью (и нао­борот). Например, предположим, что волна, изображенная на рис. 1.5, пред­ставляет собой (с точностью до ампли­туды) напряженность электрического поля в рассмотренных выше точках Рг и Р2• Поскольку пространственная ко­герентность характеризуется разно­стью фаз напряженностей в двух точ­ках в одно и то же время, то, как легко видеть, эта разность фаз всегда равна нулю. Таким образом, пространствен­ная когерентность между точками Рг И Р2 будет полной, хотя волны, проходящие через каждую из точек, имеют лишь частичную временную когерентность. В качестве второго примера до­пустим, что волны, проходящие через точки Рг и Р2, имеют все тот же вид, представленный на рис. 1.5, но при этом моменты фазовых скачков и их вели­чины абсолютно некоррелированы. Эта ситуация продемонстрирована на рис. 1.6, где построена зависимость от времени фаз фх(£) и ф2(£) двух волн. По­скольку по-прежнему степень пространственной когерентности определяется разностью фаз напряженностей в двух точках в одно и то же время, то из рис. 1.6 нетрудно заметить, что эта разность является случайной величиной. Таким образом, имеет место полное отсутствие пространственной когерентно­сти между двумя рассматриваемыми точками, хотя волны и характеризуются частичной временной когерентностью.[3]

В заключение этого раздела подчеркнем, что понятия временной и про­странственной когерентности позволяют охарактеризовать только когерент­ность лазерного излучения первого порядка. Свойства когерентности выс­ших порядков будут рассмотрены в главе 11. Подобное рассмотрение весьма важно для всестороннего выявления различий между классическим источ­ником света и лазером. Будет показано, что за счет различий в соответствую­щих свойствах когерентности высших порядков лазерное излучение дейст­вительно принципиально отличается от света обычных источников.