КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И УСИЛЕНИЯ
Для того чтобы рассчитать поглощение с учетом закона сохранения к±, необходимо вначале ввести объединенную поверхностную плотность переходов, или состояний, р2В так, что р2Л(Иг± дает отнесенное к площади поперечного сечения КЯ число разрешенных переходов или связанных переходами состояний с величиной к±, заключенной между к± и + йк±. Поскольку переходы на рис. 3.23 могут происходить только вертикально и при этом = О,
То эта величина равна также поверхностной плотности состояний в валентной зоне или зоне проводимости, относящихся к тому же элементарному интервалу с1к±. Таким образом, используя соотношение (3.3.6), получаем:
Рл=Р 1°=к1/п. (3.3.17)
Рассмотрим теперь два заданных состояния с энергиями Е^иЕ'^, принадлежащие, например, подзонам с п = 1 соответственно в зоне проводимости или в валентной зоне. Из рис. 3.236 и соотношения (3.3.3) видно, что разность энергий Е0 = Лу0 =Е>2~ Е[ определяется как
К2к2
Е0=Е8 + ^+АЕ1у (3.3.18)
Где тг — приведенная эффективная масса, а АЕХ = Е1с + Е1и. Если теперь ввести поверхностную плотность состояний р5£о в шкале энергий Е0У то можно записать:
Р^Ео^о =р5£<2Дг± =*±<гА±/я, (3.3.19)
Где было использовано соотношение (3.3.17). Величина к^к± может быть получена при дифференцировании обеих частей равенства (3.3.18). Исполь-/ зуя соотношение (3.3.19), определяем:
|
02В |
![]() Тг/пН2.
Тг/пН2.
Если теперь дополнительно ввести поверхностную ПЛОТНОСТЬ СОСТОЯНИЙ нуУо в шкале частот переходов у0, то, поскольку снова должно выполняться^ равенство р2^Уо=р^о<£Ео> из (3.3.20) получим:
Р2?о=4л тг/Н. (3.6.21)
Расчет общего поглощения падающей электромагнитной волны с Частотой V можно провести таким же образом, как это было проделано для объемного полупроводника, т. е. с помощью соотношений (3.2.30) — (3.2.32), в которых величину р^у0) следует заменить на (р*во /Ь2), являющейся в рассматриваемом случае объемной объединенной плотностью состояний. Снова предполагая, что переходы между любыми двумя состояниями являются бесконечно узкими, из соотношений (3.2.34) и (3.2.35) нетрудно получить коэффициент поглощения для переходов (п = 1) —»(п = 1) в КЯ в виде:
(3.3.
|
П2В Ре/1 |
|
( 2л2 у V2 пе0сЬ) 3 |
|
И2 ) |
|
|
|
|
Где через Е[ и Е% обозначены теперь энергии двух состояний, частота перехода между которыми равна V. При выполнении закона сохранения к± величины Ег2 и Е{ нетрудно определить с помощью рис. 3.236и соотношения (3.3.18), полагая у0 = V.
Пример 3.11. Расчет коэффициента поглощения для квантовой ямы в СаАз/АЮиАв. Рассмотрим вначале случай Т = ОК. При этом все валентные подзоны заполнены, а все подзоны проводимости пусты, так что /„(£{) = 1и£(£2) = 0. Коэффициент поглощения в этом случае максимален и равен
Атах _( 2Л2У "| Ц2 Р5у
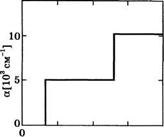
А его зависимость от энергии фотона в наибольшей степени определяется величиной р^. Зависимость коэффициента поглощения в КЯ от разности между энергией фотона и шириной запрещенной зоны (Е - Её), рассчитанная из (3.3.23) для ширины ямы Ь2 = 10 нм, показана на рис. 3.27. Из рис. 3.25а видно, что равна нулю для таких энергий фотона, что Е < Её + Е1с + ЕХи = Её + АЕх. Таким образом, в случае (Е - Её) < АЕг поглощения не ожидается. Снова полагая тс = 0,067т0 и тХ) = 0,46т0, из примера 3.8 получаем АЕг = Е1с + Е1о = 65 мэВ. При АЕг ^ (Е - Её) ^ АЕ2, где АЕ2 = Е2с + Е2о9 объединенная плотность состояний р§^ задается соотношением (3.3.21) с у0 = V, а коэффициент поглощения имеет постоянную величину, равную
8тг3 (ь2гпг
(3-3.24)
Где X = c/v. В соответствии с примером 3.6 возьмем [iav = [ц2/3]1/2 = 0,68 • 10~25 К • м, тг = 5,37 • 10~32 кг, п = 3,64 и X = 833 нм. Тогда из (3.3.24) получим aQw =5/250 см-1. При (Е - Eg) ^ АЕ2 начинают происходить также переходы между подзонами с п = 2, объединенная плотность состояний удваивается (см. также рис. 3.25а), а коэффициент поглощения также увеличивается в два раза. Отметим, что, поскольку Е2с = 4Е1с и E2v = 4Elv выполняется соотношение АЕ2 = 4ДЕх = 260 мэВ. (Уместно теперь сравнить рис. 3.27 и рис. 3.16.)
|
|
|
Рис. 3.27 Упрощенная зависимость коэффициента поглощения а от разности между энергией фотона и шириной запрещенной зоны для КЯ шириной 10 нм в ОаАз/АЮаАв |
|
100 200 300 (E-ьy [мэВ] |
|
(3.3.25) |
![]() Аналогичным образом можно продолжить описание для случая вынужденного излучения в КЯ. Легко показать, что соответствующие соотношения для коэффициента усиления получаются из (3.3.22) путем перестановки местами индексов с и и, 1 и 2. При этом получим:
Аналогичным образом можно продолжить описание для случая вынужденного излучения в КЯ. Легко показать, что соответствующие соотношения для коэффициента усиления получаются из (3.3.22) путем перестановки местами индексов с и и, 1 и 2. При этом получим:
|
( 2л2v> |
| И2 |
ГрЗП |
|
nz0chj |
1 3 |
U J |
|
§QW |
Необходимым условием положительного общего усиления снова является выполнение неравенства Ъ(Е2) из которого опять следует условие
Бернара-Дюраффура Н = Е2- Е[ ^ Е'Рс - Е'Ги. С другой стороны, величина должна быть больше, чем Её + АЕи так что
Ее+АЕ^ку^Е'р'-Е'ъ, (3.3.26)
И этими неравенствами определяется ширина линии усиления. Из (3.3.26) следует, что условие прозрачности имеет вид:
Е'Рс -Е’ъ =Её+АЕ1. (3.3.27)
Пример 3.12. Расчет концентрации прозрачности в квантовой яме в СаЛв. Из рис. 3.23 (см. также соотношение (3.2.3)) получаем, что
Е'рс = Ерс + Её и Ери = - Ери.
Условие (3.3.27) в новых переменных Ерс и Еро преобразуется, с использованием соотношения АЕг = Е1с + Е1о, в более простое выражение:
(ЕРс - Е1с) + (ЕРи - Е1и) = 0. (3.3.28)
|
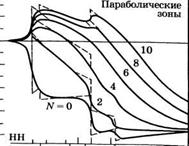
При заданной концентрации инжектированных носителей N (в 1018 см-3) в качестве параметра, |
|
Рис. 3.28 |
|
Зависимости коэффициента усиления (или поглощения) от энергии фотона |
|
Рассчитанные в приближении |
|
8 нм в СаА8/А10 2Са0 8Аб |
|
------------ ' и, г. и^о— (с разрешения, из [В]) |
|
|||
|
|||
|
|
||
|
|||
|
|||
|
|||
 |
|||
|
|||
|
![]()
![]()
Ми в плотностях состояний в объемном полупроводнике и в полупроводниковой КЯ (см. рис. 3.25а) [16]. Отметим, однако, что в полупроводниковых КЯ — как в ОаАз/АЮаАв, так и в Гп^Оа^Ав^Р^/ГпР — линейная зависимость ёр от N выполняется с меньшей точностью, чем в соответствующих объемных полупроводниках. Действительно, график зависимости ёр от N при данной температуре показывает, что при достаточно высокой величине N происходит насыщение ^ [14], причем этот эффект также в основном связан с различиями в плотностях состояний в двух сравниваемых полупроводниковых гетероструктурах. Наконец, напомним, что выражение (3.3.29) определяет коэффициент усиления в веществе, в котором находится КЯ. Вопрос
О том, как эта величина связана с коэффициентом усиления моды полупроводникового лазера, изготовленного на основе КЯ, а также реальные преимущества таких лазеров будут рассмотрены в главе 9 (см. раздел 9.4.4).