ИЗМЕРЕНИЕ ПРОСТРАНСТВЕННОЙ И ВРЕМЕННОЙ КОГЕРЕНТНОСТИ
 Весьма простым способом измерения степени пространственной когерентности между двумя точками световой волны является метод, в котором используется интерферометр Юнга (рис. 11.3). Этот интерферометр состоит из экрана 1, в котором имеются отверстия соответственно в точках Рг и Р2, и экрана 2, на котором свет, прошедший через оба этих отверстия, создает интерференционную картину. Точнее говоря, интерференция в точке Р в момент времени £ возникает в результате суперпозиции волн, испущенных из точек Рг и Р2 соответственно в моменты времени [£ - (Ьх/с)] и [£ - (Ь2/с)]. Следовательно, интерференционные полосы, наблюдаемые на экране 2 в окрестности точки Р, будут тем отчетливее, чем лучше корреляция между двумя аналитическими сигналами (или полями) световых волн Е[гх, £ - (Ьх/с)] и Е[г2, £ - (Ь2/с)], где гх и г2 — координаты точек и Р2.1 Если теперь Рис. п. з
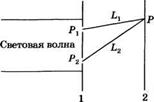
Весьма простым способом измерения степени пространственной когерентности между двумя точками световой волны является метод, в котором используется интерферометр Юнга (рис. 11.3). Этот интерферометр состоит из экрана 1, в котором имеются отверстия соответственно в точках Рг и Р2, и экрана 2, на котором свет, прошедший через оба этих отверстия, создает интерференционную картину. Точнее говоря, интерференция в точке Р в момент времени £ возникает в результате суперпозиции волн, испущенных из точек Рг и Р2 соответственно в моменты времени [£ - (Ьх/с)] и [£ - (Ь2/с)]. Следовательно, интерференционные полосы, наблюдаемые на экране 2 в окрестности точки Р, будут тем отчетливее, чем лучше корреляция между двумя аналитическими сигналами (или полями) световых волн Е[гх, £ - (Ьх/с)] и Е[г2, £ - (Ь2/с)], где гх и г2 — координаты точек и Р2.1 Если теперь Рис. п. з
|
1 Следует заменить, что время интегрирования Т в выражении (11.3.5) для корреляционной функции теперь равно времени регистрации полос (например, времени экспозиции фотопластинки). |
![]() Применение интерферометра Юнга для измерения степени пространственной когерентности электромагнитной волны между точками Рх и Р2
Применение интерферометра Юнга для измерения степени пространственной когерентности электромагнитной волны между точками Рх и Р2
Обозначить через Jmax и Jmin максимальную и минимальную интенсивности светлой и темной полосы соответственно, то в окрестностях точки Р на экране можно определить так называемую видностъ VP полос как
Vp = *max ~|min. (11.3.11)
Шах * min
Можно теперь видеть, что если оба отверстия 1 и 2 дают одну и ту же освещенность в точке Р, и если волна обладает полной пространственной когерентностью, то Jmin = 0, ивэтом случае, согласно выражению (11.3.11), вид - ность полос VP = 1. В случае, когда сигналы в точках Рг и Р2 полностью некор - релированы (т. е. некогерентны), полосы исчезают, т. е. /min = Jmax и, таким образом, видность полос становится равной нулю, VP = 0. В соответствии со сказанным в предыдущем разделе, нетрудно видеть, что величина VP должна быть связана с амплитудой функции у(1). Однако для нахождения степени пространственной когерентности необходимо рассмотреть два аналитических сигнала E[Ti, t - (Ьг/с)] и E[r291 - (Ь2/с)] в один и тот же момент времени. При этом необходимо выбрать точку Р таким образом, чтобы Ьг = Ь2. В этом случае, т. е. когда отверстия на экране дают одну и ту же освещенность в точке Р, выражение для видности полос записывается в виде (см. пример 11.1):
Vp = 1У1>(г1. г2, 0)|. (11.3.12)
С другой стороны, если два отверстия 1 и 2 дают разную освещенность (разные амплитуды сигналов) в точке Р, то вместо выражения (11.3.12) имеем:
= + Y(1)(rb г2> °)> (11.3.13)
Где (/j) и (12) — средние значения интенсивности света, прошедшего через два отверстия и дифрагировавшего в точку Р. Следует также отметить, что для произвольной точки Р, показанной на рис. 11.3, видность полос VP может определяться как |y(1)(ri> г2, т)|, где т = (Ь2 - Ьх)/с.
Пример 11.1. Определение видности полос в интерферометре Юнга. Обозначим через Е(гР, ?) поле (или аналитический сигнал) в точке Р (см. рис. 11.3) в момент времени V. Поскольку это поле определяется суперпозицией полей, пришедших из каждого отверстия (1 и 2) за время (£' - Ьг/с) и (£' — Ь2/с) соответственно, его можно записать в виде:
Е(гР, Г) = КхЕ(т19 Г-Ь1/с) + К2Е(т2, Г-Ь2/с), (11.3.14)
Где Е(г19 V - Ьх/с) и Е(г2, V - Ь2/с) — аналитические сигналы полей в точках Рг и Р2» а величины Кг и К2 представляют долю тех полей, которые попали в точку Р в результате дифракции. Множители Кг и К2 обратно пропорциональны расстояниям ЬхиЬ2и, кроме того, зависят от размеров отверстий и от угла между падающей волной и волной, которая дифрагировала на отверстиях Рх и Р2. Поскольку дифрагированные вторичные волны отстают по фазе на четверть периода относительно падающей волны (см. также обсуждение волн Гюйгенса в разделе 4.6), отсюда следует, что:
Кг = Klexp{-(jn/2)}, (11.3.15а)
К2 = K2exp{-(jn/2)}. (11.3.156)
Если теперь определить величины t1 = t'~ L2/c и I = (L2/c) - (Ьг/с)9 то выражение (11.3.14) можно записать в виде:
Е = КгЕ(rl91 + т) + К2Е(r2, t). (11.3.16)
Таким образом, согласно выражению (11.1.3) и используя соотношение (11.3.16), интенсивность в точке Р можно записать как I = ЕЕ* = = КгЕ{г1# t + т) + К2Е(г2, £)|2. Отсюда, используя выражение (11.3.15), можно получить:
I = Ix (t + т) +12 (t) + 2Ъе[К1К$Е(г1, t + т)Е* (г2, £)], (11.3.17)
Где Re обозначает реальную часть. В этом выражении величины 1и12 представляют собой интенсивности в точке Р, причем первая обусловлена излучением только из точки Рх, а вторая — соответственно излучением только из точки Р2. Эти интенсивности записываются следующим образом:
= Кг2E(rl91 + т)|2 = t + т), (11.3.18а)
/2 = W2|E(r2, t)|2 = K22I(r2, t)9 (11.3.186)
Где I(rl91 + т) и /(г2, f) — интенсивности соответственно в точках PjHP2. Усредняя по времени обе части выражения (11.3.17) и используя соотношение (11.3.7), находим:
(!) = (1г) + <I2> + ^KMRelT^irl9 г2, т)]. (11.3.19)
Здесь также использовалось выражение (11.3.15). Соотношение (11.3.19) можно записать через комплексную степень когерентности у(1), если заметить, что из выражения (11.3.8) следует:
Г<1> = W(I(rl91 + т))(/(г2, £)>]1/2. (11.3.20)
Подставляя это выражение в предыдущее и используя (11.3.18), получаем (/) = (1г) + (.I2) - I- 2((J1)(J2))1/2Re[y(1)(r1, г2, т)]. Далее из соотношения
(11.3.9) получаем:
(!) = (1г) + <I2> + 2((/1>(/2»1/2|y(i)|cos[<ю>т - ф(т)]. (11.3.21)
Теперь, поскольку и |у(1)(г1, г 19 т)|, и ф(т) являются медленно меняющимися функциями, изменение интенсивности (I) в зависимости от изменения положения точки Р (или картины полос) определяется быстрым изменением члена, содержащего косинус с аргументом (со)т. Таким образом, в окрестности точки Р имеем:
/шах = <Л> + (h) + WiXIjrW, (11.3.22а)
Fmin = W + </2> - 2((11>(/2»1/2|у(1>|. (11.3.226)
Следовательно, из выражения (11.3.11) получаем:
В случае, когда т = (Ь2/с) - (Ьг/с) = 0, выражение (11.3.23) сводится к соотношению (11.3.13).
|
|
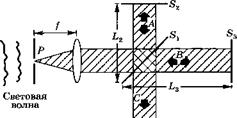 Рис. 11.4
Рис. 11.4
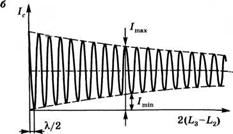
А) Интерферометр Майкельсона для измерения степени временной когерентности электромагнитной волны в точке Р; б) зависимость интенсивности света, выходящего в направлении распространения волны С, от разности Ь3 - Ь2 между длинами плеч интерферометра
Интерферометр Майкельсона (рис. 11.4а) дает очень простой способ измерения временной когерентности. Пусть в некоторой точке Р требуется измерить временную когерентность волны. Оптическая система, состоящая из экрана с небольшим отверстием в точке Р и линзы, главный фокус которой совпадает с этой точкой, позволяет преобразовать падающую волну в плоскую (см. также рис. 11.12). Эта волна затем падает на частично отражающее зеркало в! (с коэффициентом отражения Б = 50%), которое расщепляет ее на две волны А и В. Эти волны отражаются назад зеркалами 52 и 53 (В, = 100%) и затем складываются, образуя волну С. Поскольку волны А и В интерферируют, освещенность в направлении распространения волны С будет либо больше, либо меньше в зависимости от того, четному или нечетному числу полуволн равна величина 2(Ь3 - Ь2)- Очевидно, что такая интерференция будет наблюдаться только до тех пор, пока разность (Ь3 - Ь2) не станет настолько большой, что два пучка АиВ окажутся некоррелированными по фазе. Таким образом, для частично когерентной волны зависимость интенсивности 1С волны С от величины 2(Ь3 - Ь2) имеет вид, показанный на рис. 11.46. В этом случае можно снова определить видность интерференционных полос УР(т) с помощью выражения
(11.3.11) для некоторого значения разности (Ь3 - Ь2) между длинами плеч интерферометра, т. е. для данного значения задержки х = 2(Ь3 - Ь2)/с между двумя отраженными волнами, причем значения /тах и /т1п определяются в соответствии с рис. 11.46. Таким образом, величина УР является функцией задержки х и, как в случае интерферометра Юнга, связана со степенью временной когерентности. Можно показать, что в этом случае она имеет вид:
^р(т) = /у(1>(г, г,х)/, (11.3.24)
Где г — координата точки Р. Следовательно, теперь измерение видности интерференционных полос Ур(%) = |у(1)(х)| позволяет определить время когерентности хсо, например, как время, при котором УР(%со) = 1/2 (см. рис. 11.1). Соответствующую длину когерентности можно затем определить как Ьс = стс0• И снова, обращаясь к рис. 11.1, нетрудно видеть, что величина Ьс равна уд* военной разности (Ь3 - Ь2) между длинами плеч интерферометра, при которой значение видности спадает до значения УР= 1/2.