ПРИНЦИПЫ ЛАЗЕРОВ

ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ

В случае ГВГ имеем:

E(z, t) = (1/2){£шехр [/((£>£ - k01z)] + £2юехр [y(2cof - k2(0z) + с. с.}, (12.4.46)

PNL(z, t) = (1/2){PJ? Lexp [j(at-k0)z)] + P2NaLexp [j^t-h^+c. c.j. (12.4.47)

Подстановка этих выражений в (12.4.2) дает

PilL = 8odEЈ exp [-/(2ka - kzJz], (12.4.48a)

P»L = 2s0dE2aE^ exp C-yCASta, ~2kjz]. (12.4.486)

Затем, подставляя выражения (12.4.48) в (12.4.28) и пренебрегая потеря­ми в кристалле (т. е. полагая стг = 0), получаем:

^ = - j-*-dE*exp (jAkz), (12.4.49a)

Az Щ&с

^ = - j-~^dE2(aE* exp (-jAkz), (12.4.496)

Аг

Где Ak = fe2(o “ 2&ю. Уравнения (12.4.49) являются основными при описании процесса ГВГ. Для их решения было бы удобно определить новые полевые переменные следующим образом:

£;=001/2£ю, (12.4.50а)

EL=(n2j1/2E2<a. (12.4.506)

Отсюда видно, что поскольку интенсивность /ю волны с частотой со про­порциональна произведению ЕЫ |2, то величины | El |2 и/ю также являют­

Ся пропорциональными, но теперь коэффициент пропорциональности не за­висит от показателя преломления. Подстановка выражений (12.4.50) в (12.4.49) приводит к следующим уравнениям:

^2() -—I______ i(Akz} (12.4.51а)

Dz lSH К(0) Ly(Aftz)J’

Exp [~j(Akz)l (12.4.516)

OK _ 7

^ К(0)

Где ^ю(О)— значение величины в точке 2 = 0 (полагается, что эта величина является вещественной), и 18Н — характерная длина взаимодействия второй гармоники, определяемая выражением:

] _^(п(а7г2(й)1^2 по ^

1зн~ 2пйЕЛ0) ’ (12.4.52)

Где X — длина волны, а2£ю(0) — амплитуда поля основной волны на частоте со (также является вещественной). Следует заметить, что преимущество ис­пользования новых переменных Еа и Е2(й с очевидностью следует из выраже­ний (12.4.51), поскольку они содержат один единственный параметр свя­зи 18Н. Из уравнений (12.4.51) получаем условие:

А 1Е21Л I2 _ ^1-Ещ|2 (12.4.53)

С1г йг

Которое представляет собой соотношение Мэнли-Роу для процесса ГВГ. Из этого соотношения видно, что, например, уменьшение мощности или интен­сивности пучка на частоте со, должно приводить к увеличению (в тех же про­порциях) мощности или интенсивности пучка на частоте 2со. Таким образом, в рассматриваемом случае возможно 100%-ное преобразование мощности основной волны в мощность излучения второй гармоники.

В качестве первого примера рассмотрим решение системы уравнений (12.4.51) для случая, когда фазовое рассогласование столь велико (т. е. 15НАк ^>1), что во вторую гармонику преобразуется лишь очень небольшая доля мощности основной волны. Поэтому в правой части уравнения (12.4.51а)

Следует положить Еа (г) = Е£ (0). Полученное уравнение нетрудно проинтегри­ровать, используя граничное условие Е2а)(0) = 0, в результате чего находим:

(12.4.54)

«Я

Отсюда нетрудно видеть, что

Аіп2(АМ/2) (АЫ$н / 2)2

(12.4.55)

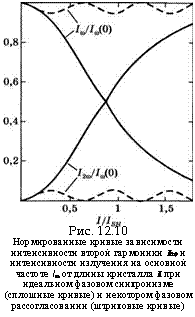Поскольку величина | Е2(й 2 пропор­циональна интенсивности 12(0 второй гармоники, из последнего выражения несложно получить зависимость этой интенсивности от длины кристалла I. В соответствии с (12.4.53) зависимость интенсивности /ю от I должна быть та­кой, чтобы выполнялось равенство I, + /2со = /„(0). На рис. 12.10 в виде штриховых кривых приведены графи­ки зависимостей относительных вели­чин [/ю//ю(0)] и [/2«/Гю(0)] ОТ парамет­ра 1/1зн ПРИ = Ю. Заметим, что

Вследствие большого фазового рассогла­сования эффективность преобразова­ния во вторую гармонику будет очень низкой. Также отметим, что с помощью (12.4.55) нетрудно показать, что пер­вый максимум величины [/2юДю(0)] Д°с“ тигается при I = 1С, где 1С — длина коге­рентности, которая определяется выра­жением (12.4.10).

В качестве второго примера рассмотрим решение уравнений (12.4.51) для случая, когда имеет место идеальный фазовый синхронизм (Л& = 0). В этом случае может происходить довольно заметное преобразование во вторую гар­монику и, следовательно, здесь необходимо учитывать «истощение» основно­го пучка (т. е. пучка на основной частоте). Таким образом, при решении урав­нений (12.4.51) больше нельзя полагать Е^(г) = Е^( 0). Однако если А к = 0, то из уравнений (12.4.51) можно показать, что при вещественной величи­не Е^(0) величина Е^(г) также является вещественной, а Е2(0(г)— мнимой. Таким образом, можно записать:

К=К1 (12.4.56а)

ЕЬ=ЧЕЬ- (12.4.566)

При этом уравнения (12.4.51) принимают вид:

Д|К1_ 1 КМ (12.4.57а)

(1г 18Н К(0) ’

Dz lSH ' K(0)'

Решения уравнений (12.4.57) с граничными условиями

Е'а (2 = 0) = £; (0) и Е'2а (О) = о

Записываются в виде:

|=EUO)tanh(z/lSH), El=EUO)sech(z/lSH).

Поскольку интенсивность волны пропорциональна квадрату амплитуды Е'2, можно записать следующие соотношения:

W4(0)=|£20012 /^2(0)ИІш//Ю(0)=|£; I2 /Е*(0).

Вычисленные с помощью выражений (12.4.58) зависимости величин 12ы/1(ь(0) и /ю//ю(0) от длины кристалла представлены на рис. 12.9 в виде сплошных кривых. Следует заметить, что при I = 18Н во вторую гармонику преобразуется значительная доля (~59%) падающей волны. Это наглядно показывает роль параметра 18Н как характерной длины взаимодействия вто­рой гармоники. Согласно выражению (12.4.52), ее величина обратно про­порциональна квадратному корню от интенсивности пучка на основной час­тоте со. Следует также заметить, что когда I 18Н, излучение накачки в соответствии с соотношением Мэнли-Роу (12.4.53) может быть полностью преобразовано в излучение второй гармоники.