ПРИНЦИПЫ ЛАЗЕРОВ

ФЛУКТУАЦИИ ЧАСТОТЫ ГЕНЕРАЦИИ И СТАБИЛИЗАЦИЯ ЧАСТОТЫ ЛАЗЕРА

Для изучения флуктуаций частоты генерации рассмотрим активную сре­ду с показателем преломления пт и длиной I, помещенную в воздушный резона­тор длиной Ь. Эффективная длина резонатора определяется как Ье = па(Ь - /) + + пт1, где па — показатель преломления воздуха. Разделим механизмы смеще­ния частоты моды на две группы:

1. Долговременные флуктуации, имеющие место в масштабе времени, скажем, более 1 с, и связанные с ними изменения длины Ь или показателя преломления па9 и которые обусловлены температурными изменениями или медленными изменениями давления окружающего воздуха.

2. Кратковременные флуктуации, обусловленные, например, акустиче­скими колебаниями зеркал, приводящими к изменениям длины резонатора, или волнами звукового давления, которые модулируют параметр па, или кратковременными флуктуациями показателя преломления пт вследствие, например, изменения силы тока разряда в газе, или воздушными пузырька­ми, присутствующими в потоке жидкости лазера на красителе. В твердо­тельных лазерах с оптической накачкой флуктуации мощности накачки при­водят к температурным флуктуациям, которые, в свою очередь, приводят к изменению показателя преломления и, следовательно, к изменению оптиче­ской длины резонатора.

В качестве примера того, как долговременные флуктуации влияют на изменения длины резонатора, рассмотрим температурный коэффициент рас­ширения а для материала (например, инвар) элементов, которые помеще­ны между двумя зеркалами резонатора. Для температурного влияния имеем |Ду£/у£| = АЬ/Ц = аД Т, где АТ — изменения температуры внутри лазера. С дру­гой стороны, медленные колебания давления также дают вклад в изменение частоты в виде = уьАпа(Ь - 1)/1 = ь(па - 1)Ар/р(Ь - /)//, где Ар — изме­нение давления р внутри лазера.

Пример 7.10. Долговременные флуктуации в резонаторе лазера. Возь­мем для инвара а = 1 • 10~6 К-1 и рассмотрим частоту, расположенную в центральной части видимого спектра, т. е. = 5 • 1014 Гц. Из предыдущих выражений находим, что изменение частоты вследствие тепловых колеба­ний составляет |Ау1| = 5 • 108 Гц • К“1. Отсюда видно, что изменение темпе­ратуры АТ даже на 0,1°С приводит к изменению частоты на -50 МГц. Для определения смещения частоты вследствие медленного колебания давле­ния отметим, что обычно для газа (Ь - 1)/1 = 0,2, подразумевая, что для воздуха па = 1,00027. Таким образом, для = 5 • 1014 Гц можно записать Ауь ^ 2,7 • Ю10Ар/р Гц. Следовательно, для относительного изменения дав­ления |Ар/р| = 3 10_3, которое может происходить в течение одного часа, имеем Avjj = 80 МГц.

________ _________________ .____________ - - ■ - п -1 IIIIIIIГ Г*

Согласно приведенному выше примеру, для уменьшения долговремен­ных флуктуаций частоты до уровня, например, 1 МГц и ниже необходимо

-О

Спектр частотного шума для КсЬУАО лазера с накачкой лазерными диодами, работающего в режиме свободной генерации (согласно работе [26])

Предел Шавлова-Таунса °<^g

J_ I 1—1—1—1______ 1_ 1—L-Ь________ І l-L. U І LJLLi

Ю1 102 103 104 106

Частота (Гц)

Использовать материал с очень маленьким коэффициентом расширения, воз­можно даже меньше, чем 1 • 10-7 • К-1, и стабилизировать температуру в пре­делах 0,01°С и меньше. Также необходимо поместить лазер в камеру, обеспе­чивающую стабильное давление.

Уменьшение кратковременных флуктуаций частоты оказывается более сложной задачей и требует наличия высококачественных виброустойчивых оптических столов и эффективной защиты от внешних воздействий. Таким образом, в целом оказывается весьма сложно уменьшить кратковременные флуктуации частоты до уровня 1 МГц и ниже. Исключение составляют мо­нолитные и компактные твердотельные лазеры, такие как Nd:YAG лазер с однонаправленным неплоским кольцевым резонатором, который был рас­смотрен на рис. 7.26 и в котором кратковременные флуктуации частоты со­ставили 10 кГц.

Для того чтобы более точно охарактеризовать флуктуации частоты гене­рации лазера, запишем выражение для амплитуды электрического поля E(t) = E0sin[2nvLt 4- срп(£)]> где vL — центральная частота лазера и функция срп(£) описывает флуктуации фазы, вызванные наличием шумов. Мгновенное значение частоты может быть записано как v(f ) = vL +dq>n(t)/2ndt = vL + vn(t), где vn(Ј) — частотный шум, который, по сути, связан с шириной линии или со стабильностью частоты и должен быть каким-либо образом описан. Результа­том измерения частотных флуктуаций является спектральная плотность мощ­ности частотного шума (см. приложение Ж), представленная функцией Sv(vm) и имеющая размерность Гц2/Гц. Здесь vm называется частотой смещения, и имеется в виду частота, при которой фаза срп(£) оказывается промодулирована шумом. На практике измеряется величина Sv(vm), где функция n(t) преобра­зуется, например, с помощью преобразователя «частота-напряжение» в сиг­нал напряжения Vn(t), и затем уже измеряется спектр мощности Vn(t) с помо­щью электронного спектроанализатора.

В качестве примера на рис. 7.28 покАзан грАфик зависимости квадрат­ного корня спектра частотного шума yJSv(vm) для монолитного Nd:YAG лазера с накачкой лазерными диодами, работающего в режиме свободной генерАции [26]. На этом же рисунке приводится предел Шавлова-Таунса для v*Sv(vm). Для лоренцевой линии, как это было предсказано теорией Шавлова-Таунса, можно показать, что спектральная плотность мощности
флуктуаций частоты, по сути, является «белым шумом», т. е. £,(ут) есть величина постоянная и задается как [27]

Зу(Ут) = Ау£/я, (7.10.1)

Где Ауь — ширина линии (заданная выражением (7.9.2), согласно теории Шавлова-Таунса). Следует отметить, что значительное увеличение уровня шума на частотах смещения меньше, чем 100 кГц, связано с акустическими возмущениями и флуктуациями мощности накачки.

Для большинства сложных применений, например при детектировании гравитационных волн, спектр шумов лазера должен быть максимально умень­шен, и в таких случаях необходимо использовать методы активной стабилиза­ции длины резонатора. Для этого одно из зеркал резонатора устанавливается на пьезоэлектрическом преобразователе, и стабилизация частоты достигается за счет обратной связи по напряжению, приложенной к преобразователю по­средством соответствующей электронной цепи. Посылая часть лазерного из­лучения на частотный дискриминатор, имеющий достаточно высокое разре­шение и стабильность, и снимая на выходе флуктуации напряжения, можно получить искомый сигнал ошибки. В качестве частотных дискриминаторов зачастую используются интерферометры Фабри-Перо с высоким парамет­ром резкости (резкие линии пропускания или отражения), а также ячейки, в которых под низким давлением помещен атомарный или молекулярный газ с резкой линией поглощения. При этом резкость таких интерферометров Фабри-Перо составляет более 105, а потери на зеркалах (обусловленные по­глощением или рассеянием) составляют миллионные доли. Так, интерферо­метр Фабри-Перо длиной 1 м обеспечивает резкость линии пропускания по­рядка килогерц. Для уменьшения частотных флуктуаций зеркала в резона­торе Фабри-Перо должны быть установлены на элементах с очень низким коэффициентом расширения (например, трубках из супер-инвара или пре­цизионной керамики), кроме того, интерферометр должен быть помещен в камеру, поддерживающую стабильное давление и температуру. Однако ста­билизация частоты в случае долговременных флуктуаций может осуществ­ляться и с помощью атомарных или молекулярных линий поглощения (в ка­честве опорной частоты). При этом опорная длина волны должна быть вос­производима и независима от внешних воздействий, таких как электрические или магнитные поля, и от изменений давления или температуры. Таким образом, наиболее подходящими являются переходы в атомах или молеку­лах (не имеющих постоянного дипольного момента), таких как СН4 для пе­рехода 3,39 мкм или 12912 для перехода 633 нм в Не-Ые лазере. Для газа или пара с низким давлением ширина линии поглощения ограничена доплеров - ским уширением и составляет около 1 ГГц (в видимом диапазоне длин волн). Для достижения более узкой ширины линии (например, порядка килогерц) необходимо использовать инструменты бездоплеровской нелинейной спек­троскопии [28].

Наиболее распространенным способом стабилизации частоты генерации является метод Паунда-Древера [29], в котором небольшая часть выходно­го пучка подвергается частотной модуляции и затем пропускается через час­
тотный дискриминатор, например интерферометр Фабри-Перо или поглощаю­щую ячейку. Для понимания принципов работы данного метода необходимо вначале отметить, что любой элемент, используемый в схеме, может вносить вклад в изменение фазы падающей волны, которое, в свою очередь, зависит от длины волны входного излучения. Для упомянутого интерферометра Фабри - Перо сдвиг фазы может быть рассчитан из выражения (4.5.4). Для поглощаю­щей ячейки изменение фазы может определяться как ф = 2пп1/'ку где I — дли­на ячейки, п — показатель преломления среды. Для лоренцевой линии по­казатель преломления п может быть связан с коэффициентом поглощения среды а через дисперсионное соотношение:

(7.10.2)

Где п0 — показатель преломления, соответствующий значительной отстрой­ке частоты от резонансной линии, V — частота электромагнитной волны, у0 — частота перехода и Ау0 — ширина линии. Следует отметить, что при

V = у0 имеем п = п0> т. е. в этом случае переход не вносит вклад в показатель преломления. Для неоднородной линии необходимо учитывать сдвиг фазы (на частоте у), вносимый всеми атомами с соответствующими частотами пе­реходов Уо, распределения которых определяются функцией ё*(Уо-Уо)- Да­лее, показатель преломления среды определяется из выражения (7.10.2), подразумевая усреднение по частотному распределению £*(уо - у0)- Таким образом, получаем:

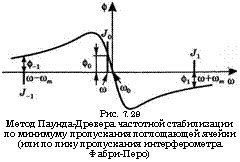
Пе" =1+!тгу рд^а*(у-''о)£Чуо(7.10.3)

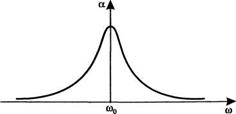
Где АТ* — полная населенность основ­ного состояния, ал — однородное се­чение. Согласно выражению (7.10.2) или (7.10.3), для заданной линии по­глощения а = а(со - со0) (см. рис. 7.29а) соответствующий сдвиг частоты можно оценить из рис. 7.296. Для простоты сдвиг фазы на централь­ной частоте линии, ф0 = 2пп01/Х, бе­рется равным нулю. Для интерфе­рометра Фабри-Перо используется аналогичная кривая. Таким обра­зом, график на рис. 7.29 позволяет получить общее представление о фа­зовом сдвиге, который возникает в частотном дискриминаторе (погло­щающей ячейке или интерферомет­ре Фабри-Перо).

Рассмотрим теперь частотно про - Модулированный пучок и запишем

Выражение для напряженности электрического поля в виде E(t) = Е0ехр [усо^ + + /Tsin сomt], где Г — коэффициент фазовой модуляции и сот — частота моду­ляции. Далее рассмотрим этот пучок в представлении функции Бесселя и запишем:

+оо

E(t) = E0ei(at £ „ Jn (Г )ei™nt, (7.10.4)

Где Jn — функция Бесселя порядка п. Если ограничить рассмотрение первы­ми двумя боковыми полосами частот ±сот, то из выражения (7.10.4) получим:

E{t) = E0e^[-J1(Г)е + (7.10.5)

Где используется свойство функции Бесселя c/_i(r) = - J1(r). Таким образом, напряженность электрического поля на выходе частотного дискриминатора будет определяться выражением:

ЕЦ) = Е0е^[-^(Г)е-^-Я-1 +J0(r)e~iп° + ], (7.10.6)

Где ф0, ф_х и фх — фазовые сдвиги, соответствующие несущим частотам для двух упомянутых полос ±сот (рис. 7.296). Если пучок после дискриминато­ра направить на квадратичный детектор, то зарегистрированный фототок будет пропорционален величине ЕЕ*, где Е* означает комплексно сопря­женную величину. Компонента фототока на частоте сот будет пропорцио­нальна величине

(ЕЕ*)ат =2Е0 |2 Ке{^1^Ифо~ф1) -e^-i-Фо)]}, (7.io.7)

Где Re означает реальную часть. Если теперь несущая частота со волны совпа­дает с центральной частотой дискриминатора со0 = 2яу0, то ф0 = 0 и ф_1 =

(см. рис. 7.29). Далее, из выражения (7.10.7) получаем (ЕЕ*)^т =0. С другой стороны, для случая, когда со Ф со0, при условии сот 2яЛу0, можно записать: ф_х = —фх; тогда из выражения (7.10.7) получаем:

(ЕЕ*)Ют =-4|£0|2 ^ое1г81п(фо)8ш(ют«-ф1). (7.10.8)

Таким образом, знак компоненты фототока на частоте сот будет зави­сеть от знака ф0, т. е. от того, выше или ниже находится частота со относи­тельно частоты со0. Данная компонента может быть затем использована в качестве сигнала ошибки в петле обратной связи, для того чтобы скоррек­тировать несущую частоту волны на центральную частоту дискриминато­ра. При этом точность, с которой это можно реализовать, зависит от коэф­фициента усиления в петле обратной связи и от ширины этой линии уси­ления.

При использовании очень точных узкополосных частотных дискрими­наторов (Лу0 = 30 кГц) можно обеспечить частотный сдвиг в диапазон© 100 мГц [30].