ФАЗОВАЯ СКОРОСТЬ, ГРУППОВАЯ СКОРОСТЬ И ДИСПЕРСИЯ ГРУППОВОЙ ЗАДЕРЖКИ
Сначала рассмотрим плоскую линейно-поляризованную монохроматическую электромагнитную волну на частоте со, распространяющуюся вдоль оси г в прозрачной среде. Тогда электрическое поле волны £(£, г) можно записать как Е = А0ехр[у(со£ - Рг)], где А0 — константа, а постоянная распространения р является функцией угловой частоты со. Функция Р = Р(ю) является характеристикой данной среды и называется дисперсионным соотношением среды (см. рис. 8.25). Теперь, поскольку полная фаза волны равна ф, = со£ -
- Р2, скорость заданного фазового фронта будет такой, что элементарные приращения временной и пространственной координат сИ и йг должны удовлетворять условию = юсИ - = 0. Это означает, что фазовый фронт дви
Жется со скоростью:
|
|
(8.6.24)
Которая называется фазовой скоростью волны.
|
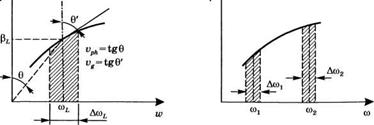
Рис. 8.25 а) Фазовая и групповая скорости в диспергирующей среде; б) дисперсия временной задержки для двух импульсов с несущими частотами и ш2; в) дисперсия групповой скорости для импульса с большой шириной линии |

|
ЗА |
![]()
|
Б |
![]()
|
ЗА |
![]()
|
В |
![]()
|
РА |
![]()
![]()
|
А |
![]()
|
Генерации Асо1< |
![]() Далее рассмотрим световой импульс, распространяющийся в среде, и обозначим центральную частоту и ширину соответствующего спектра как и Асоь соответственно (рис. 8.25а). Также предположим, что дисперсионное соотношение за пределами ширины линии можно аппроксимировать линейным соотношением, а именно Р = Рх, + (ф/^со)ю=юь(со-соь), где рь — постоянная распространения, соответствующая частоте соь. В этом случае при рас
Далее рассмотрим световой импульс, распространяющийся в среде, и обозначим центральную частоту и ширину соответствующего спектра как и Асоь соответственно (рис. 8.25а). Также предположим, что дисперсионное соотношение за пределами ширины линии можно аппроксимировать линейным соотношением, а именно Р = Рх, + (ф/^со)ю=юь(со-соь), где рь — постоянная распространения, соответствующая частоте соь. В этом случае при рас
Смотрении Фурье-представления волны, можно показать, что электрическое поле волны можно выразить как (см. приложение Г):
E(t, 2) =A[t - (z/i^)]exp[y(cDL* - рL2), (8.6.25)
Где А— амплитуда импульса, exp [y(coLf - Р^г)]— несущая волна. Величина vg задается выражением
Тот факт, что амплитуда импульса является функцией переменной t -
- (z/vg), означает, что импульс распространяется, не меняя свою форму, со скоростью vg. Эта скорость называется групповой скоростью импульса и, согласно (8.6.26), задается углом наклона зависимости со от р при со = coL (т. е. vg = tgG', см. рис. 8.25а). Также отметим, что для основного дисперсионного соотношения, такого как на рис. 8.25а, фазовая скорость несущей волны (vph = tgG, см. рис. 8.25а) будет отличаться от групповой скорости.
Согласно вышесказанному, импульс при прохождении через активную среду длиной I подвергнется временной задержке:
В предыдущем выражении была определена фаза ф, зависящая от частоты со:
Ф(со - coL) = Р(со - сoL)l, (8.6.28)
Причем ф'(со^) = [</ф(со - co^/dco]^. Поэтому величина тg = ф'(а>х,) называется групповой задержкой в среде на частоте coL.
Теперь рассмотрим ситуацию, когда в среде будут распространяться два импульса с шириной Асох и Асо2 и центральной частотой а>1 и со2 соответственно (со2 > ©!, см. рис. 8.256). Если угол наклона кривой дисперсионного соотношения отличается для двух этих частот, то оба импульса будут распространяться с различными групповыми скоростями vgl и vg2. Таким образом, максимумы импульсов достигнут начала среды одновременно, и затем, пройдя расстояние I в среде, будут разнесены во времени на величину
Ат^ = ф'(<»2) - фг(©1) = Ф"(ю1) * (®2 ~ ®i)- (8.6.29)
В последнем выражении использовалось обозначение ф'г(со1) = [с?2ф/ dco2 ]Ю1. Отметим, что соотношение (8.6.29) выполняется точно, если связь между ф и со, в диапазоне частот от до со2, можно аппроксимировать параболической зависимостью вида:
V V Sq3L
Далее рассмотрим случай, когда ширина импульса AcoL велика настолько, что дисперсионное соотношение уже не может быть описано линейным законом (рис. 8.25в). В этом случае различные спектральные области импульса будут распространяться с различными групповыми скоростями и,
|
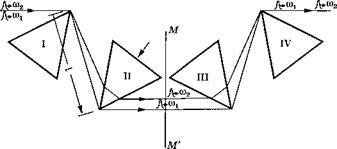
Рис. 8.26 Последовательность из четырех призм, имеющая отрицательную и контролируемую дисперсию групповой задержки второго порядка |
Следовательно, импульс будет уширяться во время распространения. Вновь предположим, что дисперсионное соотношение внутри полосы Асоь можно описать параболическим законом. Тогда согласно выражению (8.6.29) обусловленное дисперсией уширение импульса Ата будет задаваться разностью групповой задержки между самыми быстрыми и самыми медленными спектральными компонентами. Итак, согласно соотношению (8.6.29) получаем:
|
(8.6.31) |
![]() Аха = |ф"(оз£)|Дю1
Аха = |ф"(оз£)|Дю1
Величина ф"(ю£,) называется дисперсией групповой задержки (ДГЗ) среды на частоте ыь. Ее значение и определяет уширение на единицу ширины полосы импульса. Из выражений (8.6.28) и (8.6.31) можно видеть, что Ат<* также может быть записано в виде:
SHAPE \* MERGEFORMAT ![]()
|
(^оа2^ |
<*ь |
|
Ат,* =1 |
|
А со г |
|
(8.6.32) |
![]()
|
Величина |
![]()
GVD = (d2V/d2<»)GІL =[d(l/vg)/d^L (8.6.33)
Называется дисперсией групповой скорости (ДГС) на частоте соь. Ее значение задает уширение импульса на единицу длины среды и на единицу ширины полосы импульса. Следует отметить, что понятие дисперсии групповой скорости применимо только для однородной среды. Для неоднородной или многокомпонентной среды, такой как две пары призм на рис. 8.26 или многослойное диэлектрическое зеркало, рассматривать понятие дисперсии групповой скорости намного проще.