ЭЛЕКТРОННЫЕ СОСТОЯНИЯ
|
(3.2.1) |
![]() Внешние электроны атомов полупроводниковых материалов делокали - зованы по всему кристаллу, а соответствующие волновые функции могут быть записаны в виде волновых функций Блоха [4]:
Внешние электроны атомов полупроводниковых материалов делокали - зованы по всему кристаллу, а соответствующие волновые функции могут быть записаны в виде волновых функций Блоха [4]:
I|/(r) = wfc(r)[expy‘(k • г)],
|
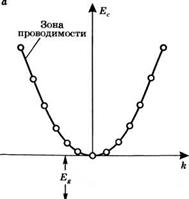
 Где uk(г) обладает теми же свойствами периодичности, что и кристаллическая решетка. При подстановке выражения (3.2.1) в уравнение Шредингера оказывается, что получаемые собственные значения энергии электрона £ являются функцией волнового вектора к и образуют зоны разрешенных значений. Здесь и ниже будем рассматривать только наиболее высокую заполненную зону, называемую валентной (относящиеся к ней величины обозначаются индексом v — от англ. valence band), и следующую, лежащую выше, называемую зоной проводимости (соответствующие величины имеют индекс с — от англ. conduction band). В приближении параболической зоны соотношение между Enk, модулем вектора к, имеет вид параболы. Это приводит к формам валентной зоны и зоны проводимости, изображенным на
Где uk(г) обладает теми же свойствами периодичности, что и кристаллическая решетка. При подстановке выражения (3.2.1) в уравнение Шредингера оказывается, что получаемые собственные значения энергии электрона £ являются функцией волнового вектора к и образуют зоны разрешенных значений. Здесь и ниже будем рассматривать только наиболее высокую заполненную зону, называемую валентной (относящиеся к ней величины обозначаются индексом v — от англ. valence band), и следующую, лежащую выше, называемую зоной проводимости (соответствующие величины имеют индекс с — от англ. conduction band). В приближении параболической зоны соотношение между Enk, модулем вектора к, имеет вид параболы. Это приводит к формам валентной зоны и зоны проводимости, изображенным на
|
|
|
------------------ Э» |
|||
|
Ч. k |
|||
|
^271/L*4* |
|||
|
Валентная |
|||
|
Зона |
|||
|
У Е |
І V |
Рис. 3.9
Соотношение между Е и к в объемном полупроводнике: з0целро-
А) положительные отсчеты энергии производятся вверх относительно дна ЗОНЫ нь1й отсчет водимости, и вниз относительно потолка зоны — в валентной зоне; б) полоЖ*1'геЛ1^1ТНОй зОНе, энеогии пгюизволится ттепх птнпгитрлкнп пптппия ияпйнтной зоны — как В
Энергии производится вверх относительно потолка валентной зоны так и в зоне проводимости
Рис. 3.9. Энергия Ес в зоне проводимости, измеренная вверх относительно ее нижнего края, или дна (см. рис. 3.9а), может быть записана в виде:
|
|
(3.2.2а)
Где тс = Н2/[с12Ес/с1к2]к=0 — так называемая эффективная масса электрона вблизи дна зоны проводимости. Аналогично энергия Еи в валентной зоне, измеренная вниз относительно ее верхнего края, или потолка (см. рис. 3.9а), может быть записана в виде:
|
|
(3.2.26)
Где т1) = Н2/((12Еи/(1к2)к=о — эффективная масса электрона вблизи потолка валентной зоны. В некоторых случаях, особенно когда рассматривается конкретный переход, оказывается более удобным отсчитывать эти энергии в одном направлении и относительно одного и того же уровня, например вверх относительно потолка валентной зоны (рис. 3.96). Если через Е' обозначить энергию в этой системе отсчета, то энергии в зоне проводимости и в валентной зоне будут, очевидно, определяться соотношениями:
|
|
||
Где Её — ширина запрещенной зоны, или энергетическая щель.
Эту простую одномерную модель легко обобщить на трехмерный случай. Обозначив через ку и кг компоненты волнового вектора электрона к, и по
Лагая, что его эффективная масса, т. е., другими словами, кривизна зоны, одинакова вдоль направлений х, у и 2, опять получаем соотношения (3.2.2) и
(3.2.3) , в которых теперь к2 =к,2+к2 +к2.
|
(3.2.4) |
![]() До сих пор при описании предполагалось, что кристалл полупроводника имеет неограниченные размеры. Для полупроводникового кристалла конечных размеров, имеющего форму прямоугольного параллелепипеда с длинами граней Ьх, Ьу и Ьх, необходимо задать граничные условия, которые сводятся к тому, что полный набег фазы волновой функции вдоль кристалла к • г должен быть кратен 2л. Отсюда получаем:
До сих пор при описании предполагалось, что кристалл полупроводника имеет неограниченные размеры. Для полупроводникового кристалла конечных размеров, имеющего форму прямоугольного параллелепипеда с длинами граней Ьх, Ьу и Ьх, необходимо задать граничные условия, которые сводятся к тому, что полный набег фазы волновой функции вдоль кристалла к • г должен быть кратен 2л. Отсюда получаем:
Кь = (2п1/Ц)у
Где I = х, у, 2, а I — некоторое целое число. Так, в изображенном на рис. 3.9 одномерном случае разрешенные состояния в валентной зоне обозначены точками, а в зоне проводимости — окружностями.
Существование валентной зоны и зоны проводимости можно объяснить, исходя из простых физических соображений. Рассмотрим, для простоты, атомы натрия, каждый из которых содержит по 11 электронов. Десять из этих электронов жестко связаны с ядром и образуют ион с положительным зарядом е. Одиннадцатый электрон движется по орбите вокруг этого иона. Пусть через Ег и Е2 обозначены энергии этого электрона соответственно в ОСНОВНОМ И В первом возбужденном электронных СОСТОЯНИЯХ, а через У! И |/2 — отвечающие им волновые функции. Рассмотрим теперь два атома натрия,
|
|
|
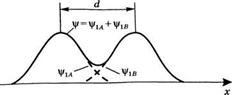
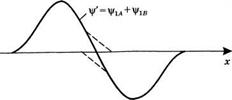
Рис. 3.10 Симметричная (а) и антисимметричная (б) линейные комбинации волновых функций Via и Vib ДВУХ одинаковых атомов, расположенных на расстоянии d |
|
Рис. 3.11 ЛГ-кратное расщепление уровней энергии отдельных атомов в системе из N атомов в зависимости от межатомного расстояния с1 |
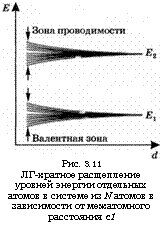 Находящихся на некотором расстоянии й друг от друга. Если величина й значительно превышает размеры атомов, то они не будут взаимодействовать между собой, так что энергии этих двух состояний будут оставаться неизменными. То же самое можно выразить по-другому, если, рассматривая, например, два атома в энергетическом состоянии Е19 представить, что энергия электрона в такой двухатомной системе по-прежнему равна Е19 а соответствующий уровень является двукратно вырожденным. Полная волновая функция может быть в этом случае записана в виде линейной комбинации двух волновых функций |/ы и |/1Б, в которой эти функции складываются либо с одной и той же фазой, либо с разностью фаз в 180° (рис. 3.10). Если потенциал взаимодействия отсутствует, то энергия обоих состояний равна Ег. Если, однако, межатомное расстояние (I становится достаточно малым, то энергии этих состояний слегка изменяются благодаря взаимодействию атомов, а двукратно вырожденный уровень расщепляется на два. Аналогично в системе из N атомов, где атомы находятся достаточно близко друг от друга, чтобы взаимодействовать, ^У-кратно вырожденный уровень с энергией Ех расщепляется на N близко расположенных уровней. Таким образом, уровень с энергией Ех приводит к образованию валентной зоны, тогда как уровень с энергией Е2 приводит, аналогичным образом, к образованию зоны проводимости (рис. 3.11). Из проведенного рассмотрения очевидно, что каждая зона в действительности состоит из N близко расположенных уровней, где N — полное число атомов в кристалле полупроводника. Поскольку число N очень велико, то отдельные энергетические уровни в каждой из зон полупроводника обычно не различимы.
Находящихся на некотором расстоянии й друг от друга. Если величина й значительно превышает размеры атомов, то они не будут взаимодействовать между собой, так что энергии этих двух состояний будут оставаться неизменными. То же самое можно выразить по-другому, если, рассматривая, например, два атома в энергетическом состоянии Е19 представить, что энергия электрона в такой двухатомной системе по-прежнему равна Е19 а соответствующий уровень является двукратно вырожденным. Полная волновая функция может быть в этом случае записана в виде линейной комбинации двух волновых функций |/ы и |/1Б, в которой эти функции складываются либо с одной и той же фазой, либо с разностью фаз в 180° (рис. 3.10). Если потенциал взаимодействия отсутствует, то энергия обоих состояний равна Ег. Если, однако, межатомное расстояние (I становится достаточно малым, то энергии этих состояний слегка изменяются благодаря взаимодействию атомов, а двукратно вырожденный уровень расщепляется на два. Аналогично в системе из N атомов, где атомы находятся достаточно близко друг от друга, чтобы взаимодействовать, ^У-кратно вырожденный уровень с энергией Ех расщепляется на N близко расположенных уровней. Таким образом, уровень с энергией Ех приводит к образованию валентной зоны, тогда как уровень с энергией Е2 приводит, аналогичным образом, к образованию зоны проводимости (рис. 3.11). Из проведенного рассмотрения очевидно, что каждая зона в действительности состоит из N близко расположенных уровней, где N — полное число атомов в кристалле полупроводника. Поскольку число N очень велико, то отдельные энергетические уровни в каждой из зон полупроводника обычно не различимы.
Подводя итог, можно сказать, что соотношения (3.2.2) и (3.2.3), вместе с граничными условиями (3.2.4), позволяют достаточно просто описать разрешенные значения энергий электронов в полупроводнике в приближении па
раболической зоны. Отметим, что в этом приближении электрон рассматривается как свободная частица с импульсом р = hk (действительно, для свободной частицы Е = р2/2т), а свойства полупроводника как реальной квантовой системы учитываются путем введения таких параметров, как ширина запрещенной зоны Eg и эффективные массы тс и mv. Отметим, что в трехмерном случае соотношение, связывающее квазиимпульс электрона р с k-вектором волновой функции, можно записать в виде:
P = ftk. (3.2.5)
Отметим также, что использование соотношений (3.2.2) и (3.2.3) предполагает, что рассматриваются только прямозонные полупроводники, в которых центры зон — потолок валентной зоны и дно зоны проводимости — соответствуют одной и той же величине k. Непрямозонные полупроводники, такие как Si или Ge, здесь не рассматриваются, поскольку они не подходят для применения в качестве лазерных сред.
|
Рис. 3.12 Валентные зоны: тяжелых дырок, легких дырок и спин-отщепленная — в ненапряженных полупроводниках групп Ш-У |
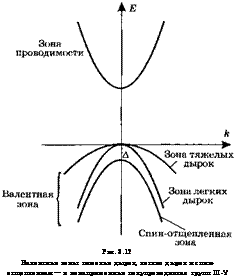 Из различных прямозонных полупроводников ограничимся соединениями групп III-V, таких как GaAs, InGaAs, AlGaAs или InGaAsP. В частности, в GaAs эффективная масса электрона в зоне проводимости составляет тс = 0,067т0, где т0 — масса покоя свободного электрона. Отметим, что во всех полупроводниках групп III-V существуют три валентных зоны разных типов, а именно зона тяжелых дырок (с индексом параметров hh — от англ. heavy holes) (mhh = 0,46m0 для GaAs), зона легких дырок (с индексом параметров lh — от англ. light holes) (mlh = 0,08m0 для GaAs) и спин-отщеплен- ная зона (рис. 3.12). Для того чтобы понять, почему это так, используя проведенное выше рассмотрение на примере атомов натрия, представим себе, что энергетические зоны складываются из дискретных уровней энергии изолированных атомов, образующих кристаллическую структуру. В этом случае можно показать, что возникает только одна зона проводимости, поскольку возбужденное состояние рассматриваемых изолированных атомов имеет такую же сферическую симметрию, как и s-орбитали атомов. Аналогично, поскольку нижнее состояние (состояние 1 с энергией Ех на рис. 3.11), как это может быть показано, имеет р-симметрию, то при различных комбинациях рх, ру и рг орбиталей р-состояния, зависящих от симметрии кристалла, образуются три валентных зоны.
Из различных прямозонных полупроводников ограничимся соединениями групп III-V, таких как GaAs, InGaAs, AlGaAs или InGaAsP. В частности, в GaAs эффективная масса электрона в зоне проводимости составляет тс = 0,067т0, где т0 — масса покоя свободного электрона. Отметим, что во всех полупроводниках групп III-V существуют три валентных зоны разных типов, а именно зона тяжелых дырок (с индексом параметров hh — от англ. heavy holes) (mhh = 0,46m0 для GaAs), зона легких дырок (с индексом параметров lh — от англ. light holes) (mlh = 0,08m0 для GaAs) и спин-отщеплен- ная зона (рис. 3.12). Для того чтобы понять, почему это так, используя проведенное выше рассмотрение на примере атомов натрия, представим себе, что энергетические зоны складываются из дискретных уровней энергии изолированных атомов, образующих кристаллическую структуру. В этом случае можно показать, что возникает только одна зона проводимости, поскольку возбужденное состояние рассматриваемых изолированных атомов имеет такую же сферическую симметрию, как и s-орбитали атомов. Аналогично, поскольку нижнее состояние (состояние 1 с энергией Ех на рис. 3.11), как это может быть показано, имеет р-симметрию, то при различных комбинациях рх, ру и рг орбиталей р-состояния, зависящих от симметрии кристалла, образуются три валентных зоны.
Так, в кристаллах кубической симметрии, к которым относятся все ненапряженные полупроводники групп III-V, ожидается, что при k = 0 энергия всех трех зон будет одинакова.
Однако спин-орбитальное взаимодействие смещает вниз одну из этих зон — спин-отщепленную зону. Поскольку величина этого смещения (например, для ОаАв АЕ = 0,34 эВ) намного превышает кТ (~ 0,028 эВ), то спин-отщепленная зона всегда заполнена электронами, которые не принимают участия в излуча - тельных или безызлучательных переходах. По причинам, приведенным в разделе 3.2.2, зона легких дырок также дает малый вклад в эти переходы. Таким образом, в первом приближении можно считать, что система валентных зон соединений групп III-V состоит только из зоны тяжелых дырок.