ДИНАМИКА ПРОЦЕССА МОДУЛЯЦИИ ДОБРОТНОСТИ
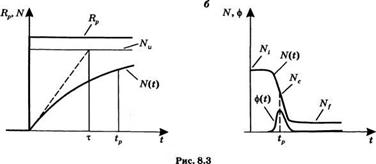
Для описания механизма модуляции добротности предположим, что накачка осуществляется в виде ступенчатого импульса, при этом начало импульса соответствует моменту времени t = 0, т. е. Rp(t) = 0 при t < 0 и Rp(t) = = Rp = const при 0 < t < tP. Предположим также, что во время действия импульса накачки затвор находится в закрытом состоянии (рис. 8.3а). При О < t < tP зависимость инверсии населенностей от времени может быть получена из уравнения (7.2.16а) для четырехуровневого или из (7.2.24а) для ква - зитрехуровневого лазера, если при этом приравнять величину ф нулю. Например, для четырехуровневого лазера получаем:
Где асимптотическая величина./V*, определяется выражением:
А^ДрТ, (8.4.2)
Которое может быть получено из (7.2.24а) в предположении, что йЫ/сИ = 0. График зависимости ЛГ(£) также приведен на рис. 8.3а. Из выражения (8.4.1) и из рис. 8.3а видно, что длительность импульса накачки £Р должна быть меньше времени жизни т верхнего состояния или, возможно, сравнима с ним по величине. Действительно, при > т большая часть накачки будет теряться вследствие спонтанной релаксации, а не накапливаться в виде энергии инверсии населенностей N(1). Из выражения (8.4.2) также видно, что для достижения значительной инверсии населенностей требуется достаточно длительное время жизни т. Таким образом, модуляция добротности может быть эффективно реализована в лазерах с переходами, запрещенными в электродипольном приближении, где величина т обычно лежит в миллисекундном диапазоне. Это имеет место для большинства твердотельных лазеров (например, с активными примесными материалами N(1, УЬ, Ег, Но в различных решетках, а также с примесями Сг, например, на александрите, Сг:ЫБАГ и рубине) и некоторых газовых лазеров (например, С02 или йодном лазерах). С другой стороны, для полупроводниковых лазеров, лазеров на красителях и для некоторых газовых лазеров, имеющих важное значение (например, в Не-Ые, аргоновом или эксимерном лазерах), лазерный переход является электродипольно разрешенным, и время жизни здесь составляет от нескольких наносекунд до десятков наносекунд. В этом случае метод модуляции добротности оказывается неэффективным, поскольку для накопления достаточно большой инверсии скорость накачки Яр оказывается слишком низкой (по отношению к времени жизни верхнего состояния).
Предположим теперь, что затвор открывается очень резко, за время £ = tp9 так что потери у(£) в резонаторе будут «переключаться» с очень высокого
|
Последовательность событий в лазере с модуляцией добротности: А) идеализированный случай зависимости скорости накачки и инверсии населенностей N от времени до момента включения модуляции добротности; б) временная зависимость инверсии населенностей N и числа фотонов ф после включения модуляции добротности (быстрое включение). |
Значения, соответствующего закрытому затвору, до значения у, соответст - | вующего открытому затвору (быстрое переключение). Выберем теперь в 1 качестве начала отсчета времени момент, когда осуществляется переключение (рис. 8.36). Временные зависимости инверсии населенностей 7У(£) и числа фотонов ф(£) могут быть получены с помощью модели скоростных уравнений в предположении, что за короткое время переключения добротности резонатора можно пренебречь членом N/х, отвечающим за релаксацию. Качественные зависимости Л^(£) и ф(£) изображены на рис. 8.36. Гра - ? фик зависимости инверсии населенностей начинается с некоторого началь - | ного значения которое можно получить из выражения (8.4.1) при t = tp, | после чего это значение остается какое-то время постоянным и затем, в | результате значительного увеличения числа фотонов в резонаторе, начина - | ет снижаться. Когда АГ(£) падает до величины пороговой инверсии населен - I ностей Ыс, число фотонов достигает своего максимального значения, как это уже было показано ранее (в разделе 8.2) для случая релаксационных колебаний. Теперь, с момента переключения в лазере, будут иметь место потери, а не усиление, и, как следствие, число фотонов (и мощность импульса) уменьшится до нуля. В это же время инверсия населенностей умень - шится до окончательной постоянной величины значение которой будет определяться динамикой процесса модуляции (см. раздел 8.4.4). Следует! отметить, что временные масштабы на рис. 8.3а и рис. 8.36 сильно отличаются. Действительно, временной масштаб на рис. 8.3а определяется величиной времени жизни верхнего состояния и, таким образом, соответствует миллисекундному диапазону (обычно 100 мкс-1 мс), тогда как временной масштаб на рис. 8.36 оказывается порядка времени жизни фотонов в резонаторе (см. раздел 8.4.4) и, следовательно, лежит в наносекундном диапазоне (обычно 5-50 не). ;
До сих пор мы рассматривали динамическое поведение в режиме быстрого переключения, когда переключение потерь в резонаторе подразумевалось мгновенным. На практике быстрое переключение означает, что время пере - |
|
G, у А |
![]()
|
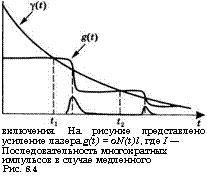
Включения. На рисунке представлено усиление лазера g(t) = oN(t)l, где I — Последовательность многократных Импульсов в случае медленного Рис. 8.4 |
|
Длина активной среды |
![]() Ключения должно быть существенно меньше времени, за которое число фотонов достигнет своего максимального значения (среднее время жизни фотонов, т. е. от нескольких десятков до нескольких сотен наносекунд). В случае медленного переключения динамическое поведение механизма модуляции оказывается более сложным, и здесь могут возникать многократные импульсы. Данная ситуация демонстрируется на рис. 8.4, где можно видеть, что потери в резонаторе у(£) уменьшаются до некоторого окончател] значения в течение достаточно тельного времени. На рисунке т
Ключения должно быть существенно меньше времени, за которое число фотонов достигнет своего максимального значения (среднее время жизни фотонов, т. е. от нескольких десятков до нескольких сотен наносекунд). В случае медленного переключения динамическое поведение механизма модуляции оказывается более сложным, и здесь могут возникать многократные импульсы. Данная ситуация демонстрируется на рис. 8.4, где можно видеть, что потери в резонаторе у(£) уменьшаются до некоторого окончател] значения в течение достаточно тельного времени. На рисунке т
Представлены временные зависимости усиления за проход £(£) = oNl и функция числа фотонов в резонаторе ф(£). Нетрудно видеть, что первый импульс берет свое начало в момент времени tl9 когда мгновенное значение спадающей кривой потерь у(£) становится равным мгновенному значению усиления £(£)• Затем этот импульс увеличивается до своего максимального значения, которое имеет место в момент времени, когда усиление (уже уменьшившееся вследствие насыщения) вновь уравнивается с потерями. После этого первого импульса усиление сбрасывается до значения, которое по величине меньше потерь, и дальнейшая генерация невозможна до тех пор, пока затвор не откроется еще больше и потери не станут меньше усиления. После чего может начать формироваться второй импульс (с момента времени t2 на рисунке), максимальное значение которого опять будет иметь место в момент времени, когда усиление (вследствие насыщения) сравняется с потерями.