ПРИНЦИПЫ ЛАЗЕРОВ

ДИФРАКЦИОННАЯ ОПТИКА В ПАРАКСИАЛЬНОМ ПРИБЛИЖЕНИИ

Рассмотрим монохроматическую волну в так называемом скалярном при­ближении, когда электромагнитные поля считаются поляризованными (на­пример, линейно или циркулярно) однородно по пространству [6]. Напря­женность электрического поля волны может быть тогда описана скалярной величиной, имеющей вид:

Е(х, у, г, О = Ё(х, у, г) ехр(усо*), (4.6.1)

Где комплексная амплитуда д должна удовлетворять волновому уравнению в скалярной форме, т. е.

{у*+к2)Ё(х, у,г) = 0, (4-6,2)

В котором к = со/с.

Решение этого уравнения для амплитуды напряженности электрическо­го поля может быть представлено в интегральном виде с использованием интеграла Френеля-Кирхгофа. При этом заданное распределение ампли­туд Ё (хг, у19 гх) в плоскости г = гх определяет их распределение Ё (х9 у, г)

В некоторой плоскости с координатой г вдоль направления распространения волны в виде:

Ё(х, у, z) = j - J, y1,z1) exP[~0'ftrH cosQdxxdyx. (4.6.3)

S

Здесь r — расстояние между точкой Рг с координатами (xl9 ух) и точкой Р с координатами (х, у) (см. рис. 4.13), 0 — угол, который отрезок РгР составля­ет с нормалью к плоскости 2 = 2и двойной интеграл берется по координатам xl9yx в плоскости 2 = 2l9 а его пределы задаются границами некоторой облас­ти S, расположенной в этой плоскости. Видно, что уравнение (4.6.3) факти­чески выражает в математическом форме принцип Гюйгенса. Действитель­но, [Ё(х19ух,21)dx1<ii/1][exp-(7fer)]/r представляет собой элементарную вол­ну, вэйвлет Гюйгенса, испущенную элементом площади dxxdyx в точке Рг; напряженность электрического поля в точке Р получается суммированием

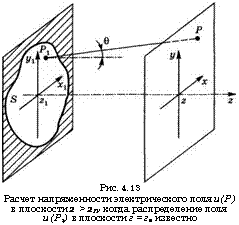Вкладов волн, приходящих ото всех точек, лежащих в плоскости г = г1в Множитель cos0, на необходимость введения которого было указано Фре­нелем, определяет эффективный раз­мер излучающего элемента площади в направлении испускания элементар­ной волны. Стоящий перед интегра­лом множитель (у*/X) — это нормиро­вочный множитель, появляющийся в результате детального теоретиче­ского рассмотрения. Он показывает, что вэйвлеты Гюйгенса сдвинуты по фазе на к/2 по отношению к волне, па­дающей на плоскость г = 2г.

Рассмотрим теперь решения урав­нений для напряженности электрического поля, либо в дифференциальной (см. уравнение (4.6.2)), либо в интегральной (см. уравнение (4.6.3)) формах, в приближении параксиальных волн (англ. paraxial-wave approximation), ко­гда предполагается, что волна распространяется вдоль оси г, а углы 0 малы. В этом случае можно записать:

Ё(х9 у9 2) = и(х9 у9 2)exp[-(jk2)9 (4.6.4)

Где и — медленно меняющаяся функция, т. е. слабо изменяющая свое значе­ние на масштабе длины волны вдоль координаты 2. В параксиальном при­ближении подстановка (4.6.4) в (4.6.2) дает:

V±u-2jk^- = 09 (4.6.5)

02

Где =(д2/дх2) + (д2 /ду2). Уравнение (4.6.5) — это волновое уравнение в

Параксиальном приближении.

Для того чтобы получить приближенную форму уравнения (4.6.3) в при­ближении параксиальных волн, положим cos 0=1иг = 2-21в амплитудной

Части сферического вэйвлета. Однако при аппроксимации фазового члена — fer следует действовать более аккуратно; действительно, возьмем расстояние г = 1 м и предположим, что это расстояние измерено с точностью Аг = 1 мкм. Для амплитудного фактора это обеспечит очень хорошую относительную по­грешность Аг/г = 10 6. Неопределенность фазы будет при этом, однако, со­ставлять Аф = kAr= 2пАг/Х9 так что при X =1 мкм это даст Аф = 2п. Это, конеч­но, неприемлемый уровень точности, поскольку, например, фазовый сдвиг Аф = п изменяет знак фазы в подынтегральном выражении. Таким образом, фазовая часть в уравнении (4.6.3) требует более высокой точности прибли­жения. Для этого представим расстояние г между точками Р0 и Р на рис. 4.13 в виде г = [(z — 2Х)2 + (х - хх)2 + (у - уi)2]1/2. В приближении параксильных волн имеем [х - хг, | у ~ Ух |] | г - 2г |. Следовательно, можно записать:

(4.6.6)

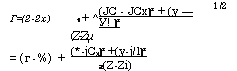Подстановка (4.6.6) в фазовую часть (4.6.3) дает при этом:

Р(г.. ,_;'expHfc(2-Zl)]

Е(х’У’2)- ц^) х

	(4.6.7)

Что представляет собой интеграл Гюйгенса—Френеля-Кирхгофа в так назы­ваемом приближении Френеля. Подстановка (4.6.4) в (4.6.7) дает:

U(x, y,z) = яL JJu(o:1,я1,z1)expj-;ft

Я ^

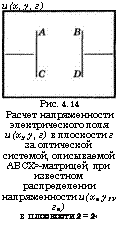Где произведена замена Ь = г - гг. Уравнение

(4.6.8) определяет напряженность электрическо­го поля, в приближении параксиальных волн, в интегральной форме, тогда как уравнение (4.6.5) определяет ту же самую величину в дифференци­альной форме. Однако, как можно показать, обе формы полностью эквивалентны.

Рассмотрим теперь в параксиальном прибли­жении распространение волны через обобщенную оптическую систему, описываемую некоторой АБС£>-матрицей, как в разделе 4.2. Обращаясь к рис. 4.14, обозначим через и(х19 Ух, 2г) и и(ху у, г) напряженности электрического поля в плоско­стях 2 = 2х и 2 = 2 соответственно перед и за опти­ческой системой. Кроме того, предположим, что

Принцип Гюйгенса справедлив для обобщенной оптической системы на рис. 4.14 при том условии, что в этой системе отсутствуют апертуры, ограни­чивающие электромагнитное поле. Это, в частности, означает, что люба линза или зеркало внутри оптической системы имеет бесконечно болыш апертуру, т. е. значительно превышающую характерные поперечные разме­ры поля.[24] Согласно принципу Гюйгенса, примененному к обобщенной опти­ческой системе, напряженность электрического поля и(х, I/, г) определяется как суперпозиция отдельных вэйвлетов, испущенных элементами плоско­сти г = гх и прошедших через систему. В результате получаем [7]:

U{x9y9z) =

S L

Что является обобщением уравнения (4.6.8). Очевидно, что при распростра­нении через свободное пространство имеем (см. табл. 4.1) А = D = 1 и В = L, так что уравнение (4.6.9) превращается в уравнение (4.6.8).