ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ

Воздействие многократно повторной нагрузки на бетон

Выносливость бетона. Для дальнейшего изложения приведем некоторые принятые основные обозначения:

N — количество циклов повторения нагрузки (база испытания бетонных образцов на выносливость); К — относительное напряжение в цикле (уровень

Напряжения), К — ;

R6 — прочность бетона, которая может быть; Rnp — призменная прочность; Ru — прочность на сжатие при изгибе; Rpu — прочность на растяжение при изгибе; Rp — прочность при осевом растяжении; q — характеристика цикла повторения нагрузки,

У------ а '

"max

Amin и ашах — минимальное и максимальное напряжение в цикле;

Ry — предел выносливости бетона (максимальное на­пряжение в цикле, при котором образец вы­держивает N циклов);

Ку — относительный предел выносливости бетона,

Предел выносливости бетона при сжатии зависит от целого ряда факторов. С увеличением числа циклов N и уменьшением характеристики цикла q предел выносливости понижается, а при увеличении частоты приложения нагрузки—повышается [30]. Для более прочных бетонов относительный предел выносливости будет выше [3]. Кроме того, на величину Ку влияют и чисто технологи­ческие факторы: назначение более низкого водоцементного отно­шения, введение воздухововлекающих добавок [27], применение для приготовления бетона белитового цемента, т. е. цемента с по­вышенным содержанием двухкальциевого силиката (2Ca0Si02), введение большого количества хлористых солей (до 9% от веса цемента) и пропаривание [16], способы укладки, условия тверде­ния, хранение и возраст бетона, качество цемента и заполнителей. Можно насчитать более двадцати факторов, влияющих на вынос­ливость бетона, но многие из них исследованы еще очень мало [10] и поэтому количественно оценить степень влияния каждого фактора на предел выносливости бетона в настоящее время еще не представляется возможным. Поэтому в действующих нормах предел выносливости пока записан зависящим лишь от прочности бетона и характеристики цикла q. При этом число циклов повто­рения нагрузки принято 2-Ю6. Но как уже указывалось, для применения железобетона в машиностроении необходимо знание предела выносливости бетона на базах, значительно превышаю­щих 2-Ю6 циклов. Рассмотрим этот вопрос подробнее.

Эксперименты по исследованию выносливости бетона на боль­ших базах пока еще фактически не проводились. Наибольшее число циклов, которое было достигнуто в лабораторных испыта­ниях, — это 107 циклов при изучении выносливости бетона на растяжение при изгибе [32] и 1,6-107 циклов при центральном сжатии [7]. Вследствие значительной трудоемкости подобных опытов, результатов испытаний по выносливости бетона для числа 44 циклов 5-Ю7—10е следует ожидать еще не скоро. Но прибли­женные значения можно было бы получить уже сейчас, если проэкстраполировать на большие базы зависимость между относи­тельным пределом выносливости бетона и числом циклов нагрузки N, полученную при N < 2-Ю6. Однако задача осложняется тем, что зависимостей Ку = / (N) существует довольно много.

Если нанести на график в координатах Ку— lg N непосред­ственно экспериментальные данные различных авторов [2 ] — [4], [6], [7], [9], [15], [16], [27], [30]- [33], включая и дан­ные авторов статьи, то получим поле точек, имеющих значитель­ный разброс. Это и естественно, так как исследованные бетоны испытывались не только по самой разнообразной методике, но также имели и различные показатели по составу, прочности, качеству цемента В/Ц (водоцементное отношение) и т. д. Приз - менная прочность бетона в этой сумме исследований в подавляю­щем большинстве случаев колебалась от 150 до 500 кГ/см2 (8% образцов имели прочность от 500 до 700 кГ/см2), расход цемента составлял от 180 до 550 кг/м3, В/Ц менялось от 0,3 до 0,8, частота приложения нагрузки колебалась от 6 до 600 циклов в 1 мин.

Следовательно, рассматривая совокупность результатов иссле­дований многих авторов, можно предположить наличие самых разнообразных сочетаний различных факторов, в том числе таких сочетаний, которые в наибольшей степени снижают выносливость бетона. Таким образом, можно наметить некоторую границу экспериментальных данных, ниже которой разрушение бетона при воздействии повторной нагрузки становится практически невозможным, несмотря на самое неблагоприятное сочетание факторов, снижающих выносливость бетона. Для этих целей был использован следующий прием.

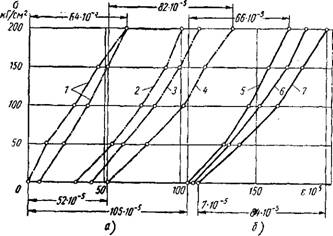
Из всей совокупности испытанных до разрушения бетонных образцов призм, балок и «восьмерок» были выбраны образцы, выдержавшие от 106 до 3- 10е циклов повторения нагрузки. Резуль­таты по этим образцам нанесены на графике фиг. 1 в координатах Ку—Q (крестиками обозначены балки, кружками — призмы, треу­гольниками — восьмерки). Проведенная огибающая кривая за­писывается уравнением

К у = 0,5 + 0.35 (1)

Если сравнить результаты различных авторов, исследовавших выносливость бетона при сжатии призм, с результатами авторов, исследовавших выносливость при изгибе бетонных балок и при растяжении «восьмерок», то относительные значения пределов выносливости окажутся численно довольно близкими. Наиболее убедительно это показал Карпухин Н. С. [7] и [9], получивший одинаковую зависимость относительного предела выносливости бетона Ку от характеристики цикла q при сжатии бетонных призм и растяжении бетонных «восьмерок». Это обстоятельство позволяет
рассматривать результаты всех авторов совместно, не разделяя их по видам действующих напряжений.

Напомним, что и в нормах степень снижения прочности при действии повторной нагрузки принята одинаковой для расчетных сопротивлений: при сжатии, сжатии при изгибе и растяжении.

Огибающая кривая в уравнении (1) практически повторяет кривую Гудмана-Джонсона с той лишь разницей, что при q = 1

Прочность бетона равна не кратковременной прочности, а длитель­ной, как это принято и другими авторами в работах [6] и [7]. Дальнейший анализ подтвердил правильность выбранного вида кривой.

Таким образом, при q = 0 Ку — 0,5; при q = 1 Ку = 0,85, что соответствует длительной прочности бетона [7]. В связи с этим из дальнейшего рассмотрения исключены все образцы, испытывавшиеся при К > 0,85.

Уравнение (1) можно записать в общем виде следующим обра­зом:

Ку = а + (0,85 — a) "I/Q5- (2)

Если же на график Ку—Q нанести показатели образцов при любом другом значении N, то вид огибающей кривой почти сохра­нится и она также может быть описана уравнением (2). Следо­вательно, можно считать, что для любого образца связь между величинами Ку и q будет выражаться уравнением (2). Например, для образца п она запишется так:

Куп = о + (0,85 — a) YQ3n ■

Решая совместно уравнения (2) и (3), получим

(1 — 1/е3) Ч - 0.85 1/еа

По этому уравнению представляется возможным для любого образца п определить величину Ку при любом значении q, если известно значение Куп при q„. Принимая q = 0 и опуская индекс п, получим формулу для пере-

Хода от значений Ку при данном q к значениям Ку0 при q = 0:

Ку— 0,85

1-УТ3

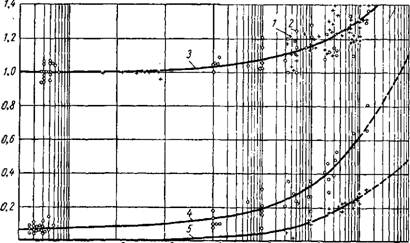
Вычисленные по формуле (5) значения Кд0 по каждой призме, каждой «восьмерке» и каждой балке показаны на фиг. 2; при этом значения Ку = 0,85 не пересчитывались.

При нанесении экспериментальных данных на график (фиг. 2) были исключены образцы, результаты испытаний которых сильно отличались от остальных, испытывавшихся при одинаковых пара­метрах. Например, в опытах Графа О. и Бреннера Е. [30] некото­рые призмы разрушались много раньше своих близнецов, несмотря

47

На меньшее относительное напряжение при одинаковом q. Так же и по тем же причинам выпали из рассмотрения некоторые резуль­таты опытов и других авторов.

Проведенная на графике (фиг. 2) огибающая кривая может быть описана уравнением

Kyo = 1 - f 0,158 In N ' которое в общем виде запишется

1 + A Ig N •

Ку 1 4- a Is N •

Следовательно, при любом значении q связь - между Ку и N будет выражаться уравнением (7). Запишем это выражение для любого образца, характеризующегося величинами Куп, Nn и q„:

TOC \o "1-3" \h \z L + а lg дгп • (8)

Решая совместно уравнения (7) и (8), получим

Ку =---------------------------------------------------------------- Г=П<---------- • (9)

1+ igjV

По этому уравнению путем пересчета данных результатов испытаний можно получить значения Ку при любой величине N и данном Q. Принимая N — 2-Ю®, получим

К =__________ к«п lg N*_________ . (10)

Kyn\gNn+ (!-*„„) 6,301 к '

Вычисленные таким образом по формуле (10) значения вели­чины Ку при N = 2-10° нанесены на графике Ку—Q (фиг. 3) кружками (призмы), крестиками (балки) и треугольниками («восьмерки»).

Решая совместно уравнения (5) и (6), получим

К =_____ 1 _________ о 85"l/o® (п)

1 0,158 lg N >

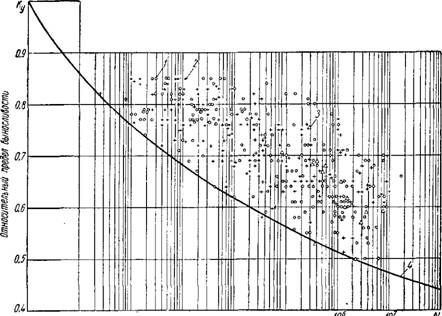
На графике Ку — Q (фиг. 3) нанесена кривая Ку = /і (q), построенная по уравнению (1), и пунктирная линия kQ6 = /2 (q), построенная по СНиП.

Сопоставляя эти линии между собой, получим

KQ6 = 1,5 Ку = + 0,85 VQs) ■ (12)

Формула [12] дает возможность определить значение коэф­фициента kQ6 в зависимости от количества циклов повторения

48
нагрузки и величины характеристики цикла. Она также показы­вает, что при значениях Ку > 0,667 коэффициент kQ6 > 1 и расчет на усталость не производится. Из графика (см. фиг. 2) также видно, что при N < 1400 циклов Ку > 0,667 при любых значениях q.

В практических целях при расчете конструкций на выносли­вость значение коэффициента kQ6, который используется для определения расчетных сопротивлений бетона на выносливость,

/ — призмы; 2 — балки; 3 — «восьмерки»; 4 — огибающая кривая К — ft (Q).

Можно принять дифференцированным в зависимости от q и числа циклов N по табл. 1, которая построена по формуле (12).

Деформация бетона при многократном повторении сжимаю­щей нагрузки. В действующих нормах [21] и [23] учет деформаций бетона, развивающихся при действии повторной нагрузки, сво­дится к назначению повышенного соотношения между модулем упругости арматуры и модулем деформации бетона. Снижение модуля деформации бетона при многократно повторной нагрузке в зависимости от марки бетона колеблется от 2,35 до 3,8 раза [3], причем это снижение относится к базе 2-Ю6 циклов. Модуль упругости арматуры принимается постоянным.

Ввиду большой важности точного учета изменения деформатив - ных характеристик бетона в период эксплуатации различных машин с железобетонными станинами при числе нагружений, гораздо большем 2-Ю6, в НИИ бетона и железобетона Госстроя СССР были проведены специальные исследования, которые вклю­чали в себя изучение деформаций бетона при воздействии повтор­ной нагрузки до 15 • 10е циклов. При этом рассматривались:

4 Сборник 1835

Влияние на изменение упругих и остаточных деформаций воздей­ствия повторной нагрузки после предварительного нагружения бетона постоянной нагрузкой; влияние возраста бетона к началу воздействия повторной нагрузки; влияние продолжительности пре­бывания бетона под длительной нагрузкой к началу действия повторной нагрузки и т. д.

Все исследования были выполнены на образцах из бетона одного состава со средней призменной прочностью, равной 490 кГ/см2, в возрасте 28 дней. Изменение призменной прочности с возрастом бетона происходило довольно слабо; в период испы­тания она составила 540 кГ/см2.

Деформативиость бетона при воздействии многократно повтор­ной нагрузки исследовалась на призмах размером 10 х 10 х X 31 см, испытывавшихся при центральном сжатии.

Призмы на многократно повторные нагрузки испытывались в специальной установке с тремя пульсирующими домкратами, работающими от одного пульсатора (фиг. 4, а). В такой установке одновременно испытывалось по три призмы — две предварительно напряженных и одна ненапряженная для сравнения 1.

Предварительное нагружение призм осуществлялось в спе­циальных пружинных установках (фиг. 4, б), позволяющих созда­вать усилия до 50 т. Максимальное напряжение при повторной нагрузке равнялось величине предварительного напряжения в пру­жинной установке для различных партий образцов и составляло

0,185 Rnp, 0,37^np и 0,555 Rnp. При действии повторной нагрузки q составляло 0,1.

Деформации ползучести бетона в пружинных установках и деформации виброползучести в установках с пульсирующими домкратами измерялись переносными индикаторами с ценой де­ления 0,002 мм (фиг. 5).

При измерении деформаций были использованы специальные репера с шариками для установки переносных индикаторов.

Реперные упоры приклеива­лись к призмам специальным составом на основе эпоксид­ной смолы. На этом клею упоры прочно держатся и не ползут под влиянием соб­ственного веса. Отсутствие ползучести было установлено приложением нагрузки в1 кГ к одному из реперов на кон­трольном образце. В течение двух месяцев показания ин­дикаторов на нагруженном и ненагр уженном реперах оставались одинаковыми.

Так как большинство кон­струкций машин из желе­зобетона выполняются пред­варительно напряженными, то полезно знать, как же будет влиять предваритель­ное напряжение, осуществ­ляемое обычно за некоторое время до ввода машины в эксплуатацию, на изменение

„„„ . .. упругих и остаточных дефор-

ФИГ, Ъ. Измерение продольных И попе - ч м т г

Речных деформаций на призмах перено - мации в период эксплуата - сными индикаторами. ции. В описываемых иссле­

Дованиях период предвари­тельного обжатия имитировался нагружением образцов в пру­жинных установках, а воздействие эксплуатационной нагрузки— испытанием образцов в пульсаторе.

Первая группа из 15 образцов была нагружена длительной нагрузкой (К = 0,37) в возрасте 34 дней. В возрасте 66 дней три призмы из этих пятнадцати были подвергнуты действию повтор­ной нагрузки. После 107 циклов эти образцы показали 9% при­роста остаточной деформации по сравнению с величиной суммар­ной деформации, развившейся в образцах-близнецах под дли­тельной нагрузкой (фиг. 6, а). 52

На слабое развитие деформаций виброползучести после пред­варительного воздействия постоянной нагрузки указывал и Лер - мит Р. [13]. В этих опытах образец после 1000 дней действия длительной нагрузки при напряжении 100 кГ/см2 был разгружен и после некоторого перерыва подвергнут действию многократно повторной нагрузки с тем же максимальным напряжением. После 3- 10е циклов остаточная деформация увеличилась на 6%. Однако, если величину деформации виброползучести отнести к величине

Деформации ползучести, проявившейся за время действия повтор­ной нагрузки, то прирост ее составит 200% (фиг. 6 б).

В возрасте 98 дней повторной нагрузке одновременно с пред­варительно напряженными образцами был подвергнут и ненапря­женный образец. После воздействия 14-10е циклов нагрузки оста­точная деформация бетона ненапряженной призмы в 7,5 раза превышала остаточную деформацию бетона предварительно на­груженных призм (фиг. 7).

Приведенные данные показывают, что предварительное напря­жение является фактором, резко уменьшающим величины оста­точных деформаций, развивающихся за время действия много­кратно повторной нагрузки.

По результатам испытаний образцов этой группы видно, что предварительное нагружение не оказало никакого влияния на величину модуля упругости. Кривые зависимости о—є подобны как для напряженного, так и для ненапряженного бетона, причем к моменту окончания действий повторной нагрузки модуль упру­гости оказался одинаковым в обоих случаях.

Развитие упругих и остаточных деформаций в зависимости~"от числа циклов повторной нагрузки по данным результатов испыта­ния всех групп образцов показано на фиг. 8.

Все значения деформаций отнесены к величине первоначаль­ных упругих деформаций ъу. Из фиг. 8 видно, что нарастание остаточных деформаций для ненапряженных образцов с ростом числа циклов происходит примерно в два с лишним раза интенсив­нее, чем для образцов, нагруженных предварительно длительной нагрузкой. Что же касается упругих деформаций, то предвари-

А*

0,5

0,6 0,7 0,8 0,9

Фиг. 9. Зависимость модуля деформации и модуля упругости бетона от количества циклов повторения нагрузки:

/ — изменение модуля деформации ненапряженного бетоиа (Eg : 2 — изменение

Модуля деформации - предварительно напряженного бетоиа (^Eg : E^j; 3 — изменение мо­дуля упругости бетона (^Еу : Е^)-, Eg — модуль деформации бетона при N > 1; У —модуль упругости бетона при N > 1; Еу~~ модуль упругости бетона при N = 1.

Тельное нагружение, как уже упоминалось, не оказало никакого влияния на их рост с увеличением числа циклов.

Сводный график средних изменений модуля упругости и мо­дуля деформации бетона с ростом числа циклов нагрузки, вы­численных по величинам деформаций, данных на фиг. 8, показан на фиг. 9. Для наглядности эти же данные приведены в табл. 2.

Кривые на фиг. 9 и данные табл. 2 показывают, что модуль деформации и модуль упругости бетона с ростом количества циклов повторения нагрузки непрерывно уменьшаются, причем это умень­шение носит затухающий характер, что хорошо видно, если по оси абсцисс количество циклов N откладывать в линейном мас­штабе, а не в логарифмическом, как это показано на фиг. 8. Однако, несмотря на затухающий характер снижения модулей, стабилизация их все же не наступает даже при очень большом количестве циклов.

Характер полученных зависимостей позволил дать экстрапо­ляцию изменения модулей до числа циклов повторения на­грузки 10®.

Пользуясь данными табл. 2, определяем изменение коэффи­циента приведения п' с ростом числа циклов приложений нагрузки для напряженного и ненапряженного бетона. Коэффициент п' представляет собой отношение модуля упругости арматуры к мо­дулю деформации бетона после воздействия повторной нагрузки. Он используется при расчете конструкций на выносливость для приведения площади арматуры к площади бетона. Вычисленные с использованием данных табл. 2 значения п' сведены в табл. 3.

Для расчета на выносливость (при N = 2-Ю6) железобетон­ных конструкций из бетона марки «500» и выше коэффициент приведения принимается равным 10. Как видно, расхождение с данными табл. 3 составляет всего лишь 4%.

Приведенные в табл. 3 вличины п' вычислены при значении модуля упругости бетона Еу = 3,2 • 10s кГ! смг и модуля упругости арматуры Еа = 2,1 • 10е кГ/см2. При других значениях Еу (при той же прочности бетона) и Еа величины п' можно определять по уравнению

Значения у принимаются по табл. 2 в зависимости от числа цик­лов N.

Полученные результаты позволяют уточнить рекомендации СНиП по выбору п с учетом числа циклов свыше 2-10®.

Изменение продолжительности предварительного нагружения перед началом действия повторной нагрузки от 31 до 170 дней не оказало влияния на величину прироста остаточной деформации, обусловленной воздействием повторной нагрузки. Это может быть объяснено тем, что образцы, даже первой группы, испытывались на воздействие повторной нагрузки в возрасте 65 дней, т. е. достаточно зрелыми, а как известно из работы [26], наиболее сильное влияние на деформацию бетона оказывает нагружение в раннем возрасте.

На деформацию ползучести возраст бетона к моменту нагру­жения оказал существенное влияние; так, например, деформации ползучести бетона, загруженного в возрасте 103 дней, были в 2 раза меньше деформаций ползучести бетона, загруженного в возрасте 34 дней, но тем не менее деформации виброползучести для обеих групп отличаются в меньшей степени.

Как уже упоминалось, образцы рассматриваемой серии испы­тывались на повторную нагрузку при трех уровнях напря­жения: 0,185 Rnp) 0,37 Rnp и 0,555 Rnp, что соответствовало максимальным напряжениям в цикле 100; 200 и 300 кГ/см2. По­давляющее большинство образцов было испытано при напряжении 200 кГ/см2, т. е. при таком напряжении, которое наиболее ве­роятно будет действовать в конструкциях машин, сооружаемых из высокопрочных бетонов. При этом во всех случаях испытания проводились при q = 0,1. Данные по величинам деформаций, полученные на образцах при напряжениях 100; 200 и 300 кГ/см2, показали, что остаточные деформации изменялись линейно для всех трех уровней напряжения, т. е. мера виброползучести для этих уровней напряжения была одинакова. Следует отметить, что исследования деформаций велись при напряжениях ниже предела выносливости бетона, определенного как в опытах авто­ров, так и в других работах [3] и [6]. При высоких напряжениях (до 0,85 RnP), применявшихся при исследовании выносливости бетона, было обнаружено, что задолго до разрушения образца (за 105—10е циклов, в зависимости от уровня напряжения) с ро­стом числа повторений нагрузки прирост остаточной деформации
по отношению к первоначальной упругой деформации начинает резко возрастать, что свидетельствует о переходе деформаций ползучести в пластические деформации II рода, обусловленные развитием необратимых микротрещин в бетоне [1 ]. Причем эти деформации уже носят ярко выраженный нелинейный харак­тер.

Проведенные исследования показали, что до определенного уровня напряжений кривые ползучести и виброползучести подобны друг другу, т. е. подкрепили ранее высказывавшиеся соображения

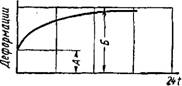
О возможности оценки величины деформации виброползучести вы­числением значения деформации простой ползучести. [1]. В своей работе Лермит Р. указывает на то, что предельная величина де­формации виброползучести не мо­жет превысить предельную вели­чину деформации ползучести под длительной нагрузкой (фиг. 10). Следовательно, если вычислить предельную остаточную деформа­цию при действии длительной на­грузки, то эта величина может быть принята за максимальную остаточную деформацию при дей­ствии повторной нагрузки. Для вычисления предельной остаточ­ной деформации Улицким И. И. в работе [24] предложен простой практический метод, принятый в строительных нормах. Мера пол­зучести г](=00, выражающая конечную величину относитель­ной деформации ползучести на 1 кГ/см2 напряжения в бетоне, определяется по приведенным в нормах данным с учетом рода цемента, возраста бетона в момент загружения, водоцемент - ного отношения, размеров сечения элементов и относительной влажности воздуха. Характеристика ползучести ср(=оо пред­ставляет собой отношение наибольшей (предельной) величины деформации ползучести к величине упругой деформации и опре­деляется

= I\T-„Ey. (13)

Кроме учтенных факторов, зависящих от свойств бетона и окружающей среды, на развитие остаточных деформаций будет влиять и характер нагрузки: режим напряжения, частота, ампли­туды и т. д., но влияние их незначительно и изучено еще в слабой степени.

Для примера приведем расчет предельных деформаций ползу­чести для клети прокатного стана «Кварто-200» *.

Расчетная величина меры ползучести т]<=00 определится как произведение ИСХОДНОЙ величины на коэффициенты

Із, Величины этих характеристик берем из работы [23, приложение 15]. Клеть изготовлялась из бетона без приме­нения ускорителей твердения на цементе активностью выше «500», причем возраст в момент создания предварительного обжа­тия составлял 28 дней. По табл. 1 приложения 15 [23] находим • Ю6 = 5,9 смУкг, В/Ц для примененного бетона было 0,35, следовательно, = 0,52; для фактического содержания цементного теста по весу 30% = 1.5. Так как клеть имеет со всех сторон гидроизоляцию, то Із — 0,6, а £4 = 1, тогда

Ті,»» -- 5,9-0,52-1,5-0,6-1 — 2,7- Ю-6 см2/кг.

По уравнению (13)

Ф(=ю =2,7-10"e-4,0-106 = 1,08.