ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ
Примеры расчета полых и сплошных цилиндров
Сопряжение полых цилиндров по торцам. Требуется рассчитать сопряжение архитрава и стен железобетонной цилиндрической станины гидропресса. Железобетонная станина совмещена с рабочим гидравлическим цилиндром. Внутреннее давление жидкости воспринимается стенами станины и цилиндрическим архитравом. Необходимо найти перемещение внутренней поверхности цилиндра в зоне уплотнений и напряжения в наиболее опасных местах конструкции.
Расчет можно разделить на два этапа: сначала рассчитать конструкцию только на нагрузку, передаваемую жидкостью на 238
стены станины, а затем на нагрузку от давления жидкости на днище цилиндра, воспринимаемую архитравом, и после этого результаты сложить. Ввиду того, что оба расчета производятся по одной методике, мы ограничимся первым случаем нагружения.
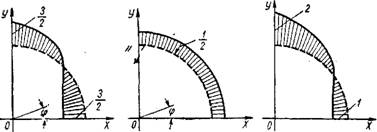
Цилиндрический архитрав станины имеет круглый канал для подвода жидкости к цилиндру, поэтому он может рассматриваться как полый цилиндр. Для упрощения расчета стены цилиндрической станины и архитрав будем рассматривать как полубесконечные полые цилиндры. Таким образом, требуется рассчитать сопряжение двух полых цилиндров разной толщины, один из которых нагружен равномерным внутренним давлением (фиг. 29).
Для приближенного расчета полых цилиндров воспользуемся формулами Фиг- 29- к расчету сопряжения
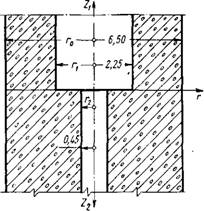
Т r J полых цилиндров разной толщины.
|
Д Е |
|
Н" = |
|
Параметры цилиндров: кв = 0,346; кн = 0,0692; г° = 6,5 м; v = 0,15. Индекс «е» означает, что величина относится к верхнему цилиндру, «н» — что величина относится к нижнему цилиндру. Подставляя в формулы (235) значения параметров верхнего и нижнего цилиндров, приведем их к виду (-ЬЁ! + 0,7516)фв; К = л. (^ш + 0,0263е)фн; |
0,265 |фв4 + (0,115+ 1,021пе + 0,376е2)уФв Е
0,00938 J ФHdl - f (0,00860 +
И" —
+ 0,03601п е + 0,01 ЗЗе2) уфн
Aez = q (—0,0239 —0,16021пе —0,0592е2) у2Ф„(т/м*)] ст» = (у (— 0,00171 — 0,00209q2 — 0,00566 lng) у2Ф„ (т/ж2);
= ^00^55 — 0,0282е + 0,0148q3 + 0,0800е1пе)у3Фв(/п/лі2); т»г = q ^3,9ЬЮ~5 — 5,63- 10"4е + 5,23- 10-у + + 2,83- 10-3е 1п е) У3ФН (т/м2).
Графики функций показаны на фиг. 30.
|
(236) |
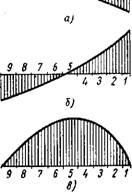
Входящая в расчетные формулы функция Ф содержит четыре произвольные постоянные, которые должны быть определены из условий монолитного сопряжения верхнего и нижнего цилиндров. Эти условия состоят в том, что в плоскости сопряжения элементов радиальные перемещения равны, вертикальные перемещения элементов отличаются только по знаку, т. е. нет раскрытия шва. Нормальные напряжения равны, а касательные напряжения отличаются только по знаку; эти условия сопряжения могут быть выполнены только интегрально, приближенно. Для их выполнения линию сопряжения разбиваем на участки, и в пределах каждого участка приравниваем площади эпюр соответствующих функций. Разбивка на участки представлена на фиг. 31. При расчете сопряжений пятый и шестой участки цилиндров не учиты - 240
Ваются, так как в пределах этих участков эпюры напряжений меняют знаки. Площади эпюр по участкам приведены в табл. 35.
|
Г) |
|
Площади эпюр по участкам сопряжения
|
В выражении Фн единицу нужно отбросить, так как нижний цилиндр не нагружен внутренним давлением. Параметры а и Ъ можно взять по графику на фиг. 6.
Ав = 2,30; ан = 2,14; ft, = 1,36; 6Н = 0,968.
Произвольные постоянные для нижнего цилиндра обозначим С3 и С4. Приравнивая напряжения и перемещения на каждом участке, получим семь систем по четыре уравнения с четырьмя неизвестными. Решая системы, найдем значения произвольных постоянных на каждом участке. Они приведены в табл. 36.
|
Таблица 36 Значения произвольных постоянных по участкам
|
Подставив значения произвольных постоянных в формулы (237), получим окончательные выражения разрешающей функции и ее производных. Эти выражения выписаны в табл. 37.
Пользуясь формулами (236) и табл. 37, можно определить напряжения и перемещения в любой точке верхнего или нижнего цилиндра. В табл. 37 обозначено g = 242
|
HJ) To со |
|
HJ) To со |
„.=
6,50
Если q = 3200 т/м2, t = з, іи-іи° т/м', то иг = ° м.
Расчет цилиндра с прямоугольной полостью. Для приближенного расчета станины в виде цилиндра с прямоугольной полостью У с целью определения необходимого
Диаметра из условий прочности воспользуемся формулами напряжений на стр. 156 при п = 2. Расчет проведем с точностью до равнодействующей нормального напряжения аг на внутреннем контуре.
Схема станины и расчетная схема показаны на фиг. 32.
По первой расчетной схеме станина нагружена только двумя вертикальными линейными нагрузками по 6300 т. По второй расчетной схеме кроме этих нагрузок приложены еще горизонтальные линейные нагрузки по 6300 т.
Задаемся г° = 6300 т 15 м
+ 1,252 = У 4,44 4,22 м; к = = 420 т/м.
2,11 м - Р ~ 6300 т. ■ 0,5. Длина станины равна
Складываем частное решение при п — 2 и напряженное состояние, соответствующее простому осесимметричному растяжению.
Полученное напряженное состояние имеет равнодействующую по оси X, равную нулю, и равнодействующую по оси Y, равную единице; для напряжений аг на контуре при q = к
Я/2
J cos2cp sin ф с/ф
[> -
=------------------------ і -
Распределенная нагрузка т! м = 199 тім2:
|
Зк-2)Є2 |
|
Da„ = |
Ф = qx = -1.199 = 298 /п/л2. График нагрузки показан на фиг. 33.
|
Фиг. 33. К определению суммарных напряжений сГф при л = 0 и я = 2. |
Определяем напряжения при расчете по первой схеме. Наибольший интерес представляет распределение напряжений сгф. Максимальные значения сгф будут на оси Y.
Dgv = З [(1 — 2/с"2 + к4) — 2 (2
— (1 2/с2 — Зк4) е"4] 298 т/м2. На внешней поверхности при q = 1
-12(1 + к2 — к"2 — /с4)-298 = —12-2,69-298 /п/л2;
3-4,94;
= - тйт-4-298 /п/л2 = -2,18-298 = 649 т/м2.
Ф 494
|
D = —3 [6 + (к4 + к-4) — 4 (к2 + к"2)] 2,69 |
На внутренней поверхности при q = к
|
298 т/м2 |
|
Ст" ~ 4,94 |
£>0ф = 3 [ 10 — (к4 + к-4) — 4 (к2 + /с"2)] 298 т/м2-, Do,, = 3-23,06-298 /п/л2; 23,06 „по „/..9, „ „ПО „ПП -/.J
-4,66-298 — —1390 т/м2.
На эти напряжения следует наложить напряженное состояние при осевой симметрии
99,5 -= 0,667-99,5 = 66,3 т/м2-,
При Q
99,5 = 1,67-99,5 = 166 тім2.
"ф - і _ . Суммарное значение сгф:
При Q = 1 0Ф = 649 + 66 = 715 т/мъ\ при q = к сгф = —1390+ 166 = — 1124 т/м2.
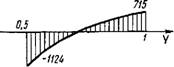
Вид эпюры сгф по оси Y показан на фиг. 34.
Вынужденные колебания полого цилиндра под воздействием нагрузки
|
700,0 |
|
0,25 t |
|
Ш - = 0,36; 0,7э |
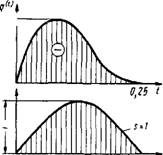
Q (t). Предположим, 'что во время испытания образца на гидравлическом прессе произошло внезапное повышение давления в цилиндре. В течение 0,25 сек давление возросло на 700 т/м2, а затем упало до прежней величины. График распределения нагрузки во времени показан на фиг. 35. Требуется вычислить увеличение радиального перемещения и напряже-
НИ я сг,
Параметры цилиндра
К =75~ и
|
0,75. |
1 — 2v
1 —V
|
1-(Г 4-0,2- 10а 1,2-0,6 Е |
|
\- v)(l — 2v) = 1,11-10" т/м2; = 3,33-106 т/м2. |
|
2\i = |
|
(1 +v) |
Модуль упругости бетона цилиндра Е — 4 • 10е т/м2. Константы Ляме X + 2ц = 4,44-106 т/м2, Е\
Вычисляем распределенную массу цилиндра. Объем 1 м цилиндра V = л (r\ — rf),
|
1 +к2 |
|
Фиг. 34. Эпюра напряжения сгф по оси Y. |
V = 3,14 (0,752 — 0,272) = 1,54 м3.
|
- 0,379 тн-сек2/мя. |
Объемный вес железобетона 2,4 т/м3, вес цилиндра (1 * по высоте) Р = 2,4-1,54 = 3,70 т.
Масса М = — - 3,70
9,81
Распределенная масса (по внутреннему диаметру) на 1 м высоты
М ___ 0,379 ______ ^ пп. тн/сек2
TOC \o "1-3" \h \z Т ^ ~2лГ ~ 6,28-0,27 ~ м3 '
Определяем скорость распространения волн:
Й = |/Щ Y — — = 0,224 тфе/ ;
Г V Ж ЛС
. й = У40а 103 = 4450 м, сек -
Вычисляем частоты собственных колебаний цилиндра:
А а 4450 ,,
= ns - pr; = - Qjg— = 5940 Усек.
|
S |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
"s |
1,50 |
5,30 |
9,81 |
14,7 |
19,6 |
24,6 |
29,4 |
|
<Ј>s |
8,92 |
31,5 |
48,3 |
87,4 |
116,5 |
146 |
175 |
(Все величины разделены на 1000.) Значения ns приняты по табл. 22 и графикам на фиг. 12 и фиг. 13 для к = 0,36.
Низшая частота собственных колебаний цилиндра 8920 гц. Разложим нагрузку q (t) в ряд по ars\
П
S
Изменение нагрузки во времени носит плавный характер, поэтому в разложении можно ограничиться двумя членами ряда. Разложение показано на фиг. 35:
Q (t) = —183 (2 sin Ш + sin 8nt) тім2;
При t = V16
Q(t) = 700 тім2,
При t = V4 -
Вычислим перемещение внутренней поверхности цилиндра. Для этого необходимо определить ^ при S = 1 И S = 2. % = 1,50; «а = 5,30 £к (кл5) = — бх4;
*в = - у 1Л Го Ю - J0 («,)];
--- - J - U1 (K'h) Yl (ns) — Y j (Ktls) J! (/i5) j.
Значения функций Бесселя берем по таблицам в работе [15] А (0,36-1,5) = 0,260; (0,36-1,5) = —1,38; (1,5) = —0,412 У0 (1,5) = 0,382; /0 (1,5) = 0,512; J1 (1,5) = 0,558; (0,36-5,3) 0,581; Yx (0,36-5,3) = —0,559; 1^(5,3) = 0,044 У0 (5,3) = —0,337; /0 (5,3) = —0,076; (5,3) = —0,346; = - J - [0,260-0,382 + 1,38-0,512] = 1,28;
= 1-0,260-0,412 + 1,38-0,558] = 1,04;
Ха = 0,581 -0,337 — 0,559-0,076] = —0,374;
= ~Г [°.581 -0,044 —0,559-0,346] = —0,280;
1,5-1,28 — 0,75-1,04 = 1,14; = _ 1,5-0,374 + 0,75-0,28 = —0,351;
<7^1 = —366-1,14 = —417 т/м2; = 183-0,357 = 65,3 т/м2;
2
|
МО |
|
£(1 |
2(1—v8) Л®
ZTffi- (417 sin Ш — 65,3 sin ШУ>
|
2(1-у_ 2-0,96.0,13-0,75 _ fi? п_6. £(1_д») ~ 4- 10е-0,87 - U. U40/-1U, 417 sin 4nt = х; 65,3 sin 8nt — у. Вычисляем радиальное перемещение
|
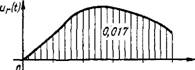
Величины иг в таблице даны в мм. График иг (t) показан на фиг. 36. Максимальное перемещение составляет величину 0,017 мм. От статической нагрузки это перемещение составило бы 0,020 мм.
Напряжение аг на внутренней поверхности цилиндра меняется по закону, показанному на фиг. 35.
|
0,05 0,10 0,15 0,20 0,25 t Фиг. 36. График иг (0- |
Вычислим максимальную величину напряжения <тф на внутренней поверхности цилиндра. Его можно вычислить по формуле (161), но эта приближенная формула в данном случае должна дать результат, близкий к статическому расчету по формуле Ляме, так как нагрузка q (t) действует довольно длительное время. При использовании формулы (161) возьмем максимальное значение ur (t) по графику на фиг. 36 и вычислим
|
0,2-0,I 0,36 |
|
2-0,13 + |
|
1,10 0,87 |
|
700,0- 885,0 т/м2. |
|
700,0 |
■(2 — 0,75-0,13)
0,87
Напряжение стф от статической нагрузки 700,0 т/м2 составило
Бы 910,0 т/м2.
|
Фиг. 37. Схема нагружения цилиндрического ЛЄНИЄМ 0Т °бМ0ТКИ ПР? ДВа' архитрава: рительно напряженной ВЫ - I - квадратная парабола; 2 - Р = 52 200 СОКОПрОЧНОЙ ПРОВОЛОКОЙ. 3 ~ 'max ~ 5320 ЭТО нагружение ПО боко - Вой поверхности вызывает равномерное сжатие во всех точках цилиндра и оно может быть учтено элементарным расчетом. Параметры цилиндра: |
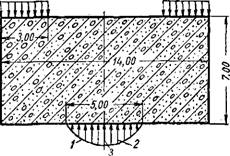
Расчет сплошного цилиндра. Рассмотрим расчет железобетонного цилиндрического архитрава пресса. Цилиндрический архитрав нагружен по торцам осесимметричной нагрузкой (фиг. 37). Боковая поверхность цилиндрического архитрава нагружена равномерным дав-
Г° = 7,0л; h = 3,5 м\ I - ~ = 0,500;
V = 0,15; Е = 4-Ю6 т/м*.
Расчет начинаем с разбивки нагрузки по торцам на сплошную равномерно распределенную и самоуравновешенную по каждому торцу. По верхнему торцу цилиндр нагружен реактивным давлением анкеров вертикальной арматуры, воспринимающей усилие штампования гидравлического пресса. По нижнему торцу цилиндр нагружен контактным давлением, передаваемым через подштам - повый блок. Закон распределения этого давления принят по квадратной параболе.
Суммарное усилие, воспринимаемое цилиндрическим архитравом, равно 52 200 т.
Интенсивность сплошной равномерно распределенной нагрузки
^ = 5я720° = 339 т/м2-
Интенсивность нагрузки в зоне реактивного давления анкеров
52 200 - n 2
Я= я (7,02 -4,0») т/м -
Интенсивность самоуравновешенной нагрузки в зоне реактивного давления анкеров
503 — 339 = 164 тім2.
По нижнему торцу максимальная ордината параболы эпюры контактного давления определена из условия, чтобы объем эпюры был равен суммарному усилию. Максимальная ордината
<7шах = 5320 тім2.
Максимальная интенсивность самоуравновешенной нагрузки в зоне контактного давления:
Яг та* = 5320 — 339 = 4981 тім2.
Уравнение параболы эпюры контактного давления Я (Q) = (5320 — 41 700q2) тім2.
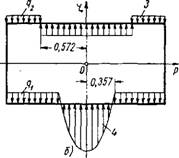
Эпюра самоуравновешенной по каждому торцу нагрузки показана на фиг. 38, б, а распределенной — на фиг. 38, а.
Расчет на равномерно распределенную нагрузку ведем по элементарным формулам.
Радиальное перемещение
339-0,15.7,00 „ „оп иг — Яі 6 = jTjQj Q = 0,089е ММ.
Осевое вертикальное перемещение
Г<> 339-7,00£ лепо* Uz = — Яі Е = 4TWT - = — °'593 Е ММ.
Все напряжения, кроме аг, равны нулю.
'°г = — Яі = - 339 тім2.
Расчет на самоуравновешенную нагрузку по торцам ведем по формулам (216) с использованием первого однородного решения. Граничные условия по торцам цилиндра удовлетворяем для напряжений а2 с точностью до момента и для напряжений хгг с точностью до равнодействующей.
|
|
|
■■ 4981 т/м1. |
^ 1
І
А)
Фиг. 38. Разбивка нагрузки на торцах архитрава на равномерно распределенную и само уравновешенную по поверхности каждого торца:
/ и 2 — qi = 339 m/ju2; 3 — q2 = 164 т/мг: 4
Вычисляем момент от нагрузки по верхнему торцу: при 0 < q < 0,572; £ = I
|
J Q2dQ |
|
ГЬ 1 |
0,572
0 5722./-®
339 ' 0 = г®-21,15 тім?-,
При 0,572 < q < 1 і
Q4Q =
|
164 3 |
|
3„ /■О<72 |
|
(1 —0,5723) Го |
|
■ го-44,44 тім2. |
0,572
Суммарный момент — 44,44 + 21,15 = —23,29г;* т/м2. Момент от нагрузки по нижнему торцу £ = —/:
0,357 0,357 1
|
MiZj. + M%Z2 = 80,68 m/м2 7\Z3 + T2Z4 = 0 |
- 532 j q4Q + 41700 J Q^Q + 339 j Q2CIQ
= —80,69 + 48,36 + 113 = 80,68г® т/м2.
Граничные условия на торцах цилиндра запишутся следующим образом:
MtZt + M2Z2 = - 23,29 т/м2 _ п „п
2 4 2 (238)
С - -0,500.
Величины Ml, М2, Ті, Т2 для первого однородного решения были определены ранее (см. табл. 34). Четыре произвольные постоянные, входящие в функции Zt, можно определить, воспользовавшись формулами (218) или из табл. 32 для единичных момен-
TOC \o "1-3" \h \z -719 2595 '1406 2379
2233 -4495 - 2608 і 014
А) 6) В) г)
Фиг 39. Графики функций:
А — Zi т/мг; б — Z, т/мг; в — Zs т/м'; г — Zt т/м'.
Тов. Не представляет затруднений определить их непосредственно из системы (238), так как она распадается, как было указано выше, на две системы по два уравнения с двумя неизвестными. Значения произвольных постоянных:
Су = 174,9 т/м2; С2 = — 1892 т/м2;
С3 = 838,7 тім2-, С4 = 612,5 т/м2.
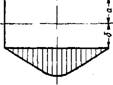
|
1955 .«гтптЛТГТТГгггт^ |
|
-1460 |
|
Фнг. 40. Эпюры напряжений а г на торцах цилиндрического архитрава: |
|
А - I = 0,5; 6-І =-0.5. |
Зная произвольные постоянные, запишем окончательные выражения функций Z
Zy = 174,9у — 18926 + 838,7% + 612,5р;
Z2 = 174,9ц + 1892Я + 838,76 — 612,5у; Z3 = 174,9Я— 1892 ц + 838,7у + 612,56; Z4 = 174,96 + 1892у + 838,7р — 612.5Я.
|
|
Значения функций у, 6, X, р и функций Z(- для различных £ приводятся в табл. 38— 40 (значения функций даны через 0,5 м). Графики функций Z; показаны на фиг. 39. Имея значения функций Ri (табл. 30) и Zt (табл. 39 и 40), по формулам (216) вычисляем.252
|
Таблица 38 Значения гиперболо-тригоиометрических функций у, б, К, (і при различных £
|
|
Значения функций Z,- при £ = 0 - з - 0,5 |
|
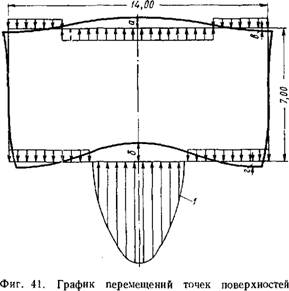
Цилиндрического архитрава: а — 1,07 мм', б —1,98; в — 0,28; г—0,52 мм; 1 — нагрузка. |
|
Таблица 39
|
|
Значения функций Z, при £ = —0,5-^0
|
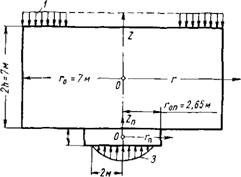
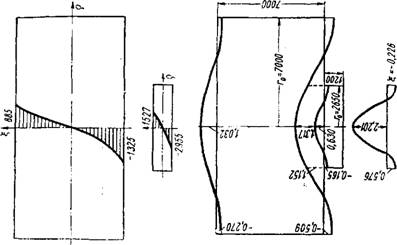
Перемещения и напряжения цилиндрического архитрава от самоуравновешенной нагрузки по торцам. Эпюры напряжений ог при I = ±1 показаны на фиг. 40. График перемещений точек поверхностей архитрава изображен на фиг. 41.
Расчет сопряжения сплошных цилиндров по торцам. В качестве примера рассмотрим сопряжение железобетонной под- штамповой плиты с железобетонным цилиндрическим архитравом гидропресса. Для упрощения будем полагать, что трение в зоне контакта отсутствует. Условия сопряжения при этом будут:
А) напряжения аг в зоне контакта равны;
Б) формы поверхностей нижнего и верхнего цилиндров в зоне контакта совпадают.
Расчет ведем в первом приближении, т. е. с точностью до первых членов последовательностей моментов. Параметры цилиндрического архитрава:
Г° = 7 м; h = 3,5 м; v = 0,15; Ей = 4-106 т/м2.
Параметры железобетонной подштамповой плиты: г° = 2,65 м; h = 0,6 м\ v = 0,15; Е& = = 4-106 т/м2.
Схема нагружения конструкций показана на фиг. 42.
|
Фнг. 42. Схема нагружения цилиндрического Архитрава и подштамповой плиты: / - q = 503 т/м'-. 2 - 2Л„ = 1,2 м\ 3 -?тах= = 8300 т/м'. |
На верхнем торце цилиндрического архитрава при £ = 0,5 приложена равномерно распределенная по кольцу нагрузка 254
интенсивностью 503 т/м2. Эта нагрузка создается реактивным давлением анкеров продольной арматуры станины цилиндрического пресса.
На нижнем торце подштамповой плиты приложена нагрузка от воздействия подштампового металлического блока. Закон распределения этой нагрузки принят по квадратной параболе. Максимальная интенсивность нагрузки 8300 т/м2. Нагрузка распределена по кругу радиусом 2 м. Суммарное усилие, равное объему эпюры нагрузки, составляет 52 200 тн. Этой же величине равен объем эпюры нагрузки, распределенной по верхнему торцу цшшндрическогб архитрава.
Сначала рассчитаем цилиндрический архитрав и подштампо- вую плиту на действие единичного момента, приложенного к одному из торцов. Расчет ведем по формулам (226) при п = 1, т. е. с использованием первого однородного решения для сплошного цилиндра.
Граничные условия на торцах цилиндрического архитрава имеют вид:
І і
I = 0,5 го J azQ2dq = a; r\ J xrzQdq = 0;
О о
І і £ = -0,5 о q4q = 0; Го§ т qdq = 0.
О о
Подставив в граничные условия формулы (226), перепишем их в виде
М& + M2Z2 = 4; 7\Z3 + T2Z4 = 0;
Ro
MJZJ + M2Z2 = 0; 7\Z3 + 7\,Z4 = 0. Здесь обозначено:
Mt-~ jR9Q2dQ; M2=jfiloQ2dQ;
О 0
1 1
Функции Zt - при С = —0,5 отмечены чертой сверху. Значения функций Ri даны в табл. 30. Интегралы (240) можно найти численным методом, заменив их суммами.
Мі = 0,04086; М2 = 0,002345; 7\ = 0,1055; Т2 = 0,06232.
Для первого однородного решения
А = 2,645; 6 = 1,377.
Вычислив значения гиперболо-тригонометрических функций (227) при £ = ±0,5, получим для определения четырех
255
Произвольных постоянных Ct систему из четырех линейных уравнений. Если сложить, а затем вычесть попарно первое и третье, а затем второе и четвертое уравнения, то система распадается на две системы по два уравнения с двумя неизвестными:
2 (0.04890С! + 0,06081С4) = ;
Го
2 (0.2186С! + 0.06245Q = 0;
2 (0,05201С, + 0,05533С2) =
Го
|
(241) |
2 (0,09470С2 + 0,2136С3) = 0.
Отсюда получим
RlC\ = — 3,049а, гоС2 = 18,20а; ГоС3 = —8,067а; ГоС4 = 10,67а.
Зная произвольные постоянные, определим Z(- при £ == ±0,5: rlZ\ = 27,19а; rlZ2 = — 50,46а
RoZ3 = 29,50а; rlZi ■= — 50,26а з з, (242)
RlZ\ = — 1,086а; roZ2= 17,38а, , £ = —0 ,5.
R\Zs = 8,637а; r03Z4 = - 14,98а J
Расчет цилиндрического архитрава на единичный момент, приложенный к нижнему торцу, при I = —0,5 можно не производить, так как величины функций Zt при этом по абсолютной величине не изменяются.
Функции Zx и Z2 ведут себя при перемене направления координатной оси как четные функции, т. е. остаются без изменения. Функции Z3 и Z4 ведут себя в этом случае как нечетные функции и меняют знак на обратный. В этом легко убедиться, рассмотрев формулы (227).
По аналогии с (242) запишем значения функций Z,- при £ — = ±0,5 при нагружении единичным моментом а нижнего торца цилиндрического архитрава.
RoZ, = - 1,086а; r%Z2 = 17,38а |
RtZ3 = —8,637а; rtZ* = 14,98а j Е ~ ' '
RoZ, = 27,19а; rlZ2 = — 50,46а 1
RoZ3 = - 29,5а; roZ4 = 50,26а j £ ~~
Теперь проделаем такой же расчет для подштамповой плиты.
Граничные условия на торцах плиты запишутся аналогично уравнению (238) с той лишь разницей, что гиперболо-три - гонометрические функции вычисляются при
Запишем в окончательном виде системы уравнений для определения произвольных постоянных С{.
2 (0,01062^ + 0,004563С4) = 4 5
Гоп
2 (0,07607с! + 0,04114С4) - 0; 2 (0,02386Са + 0,01626С3) = ~;
Ron
2 (0,1068С2 + 0,09088С3) = 0.
Находим произвольные постоянные
RlnCy = - 6,779а; г3опС2 = 105,2а;
Г2„С3 = — 123,6а; г30пС4 = 12,53а.
Определим функции Zi при £ = ±0,226:
( r3onZx = 28,99а; r3onZ2 -= — 123,2а; £ = 0,226 , ,
R30nZ3 = 100,2а; r3onZ4 = — 168,7а;
( rlnZi = —3,350л; r3onZ2 — 103,0а;
» I
Г
. ____ о 226'
|
(244) (245) |
Ь ' | r3onZ3^- 89,95а; r30nZt = - 151,3а.
Аналогичным способом найдем значения функций Z,- при действии единичного момента на нижнем торце подштамповой плиты.
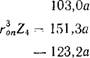
R\nZ і = — 3,350а; r30nZ2 r3onZ3 = 89,95а; r30„Z, = 28,99а; rlz2 r^Z3 - 100,2а;. r3onZ4 = 168,7а
(246)
Имея значения функций Zt от нагружения единичным моментом, нетрудно вычислить значения функций Z(- от воздействия на цилиндрический архитрав и плиту фактически приложенной нагрузки.
Для этого разобьем нагрузку на каждом торце цилиндрического архитрава и подштамповой плиты на сплошную, равномерно
17 Сборник 1835 257
Распределенную и на самоуравновешенную нагрузку по каждому торцу. Расчет на сплошную равномерно распределенную нагрузку производится по элементарным формулам; напряжения и перемещения от воздействия этой нагрузки можно будет учесть отдельно. Расчет на самоуравновешенную нагрузку по каждому торцу
Выполним, используя готовые данные расчета цилиндра на единичный момент. Разбивка нагрузки на торцах цилиндрического архитрава и подштамповой плиты показана на фиг. 43, а и б.
Находим численные значения моментов нагрузки. На верхнем торце цилиндрического архитрава при - £ = 0,5
Мч = — 23,22ло т/м2.
На нижнем торце при £ = —0,5
|
339 |
|
Шш |
|
|
|
2360 2360 5940 2360 |
|
Фиг. 43. Разбивка нагрузки: |
|
А —иа торцах цилиндрического архитрава; б — на подштамповой плите. |
Mq = 70,20ло т/м2.
|
Мс |
|
(24?) |
|
(248) |
На нижнем торце подштамповой плиты при I = —0,226
308,6ло„ т/м2.
Подставив моменты от нагрузки вместо величины а в формулы (242), (243), (245), (246), получим значения функций Zt цилиндрического архитрава и подштамповой плиты при воздействии внешней нагрузки.
|
Для цилиндрического архитрава:
|
Для подштамповой плиты:
|
S |
Zi |
Z2 |
Z4 |
|
|
0,226 |
— 1034 |
31770 |
—27750 |
46700 |
|
—0,226 |
8945 |
—38020 j —30910 |
52040 |
Кроме внешней нагрузки, в зоне сопряжения приложен неизвестный момент а, поэтому окончательные величины функций Zt
Получим, прибавив к значениям Z,- по табл. (247) и (248) величины функций Z, от действия единичного момента а. Воздействие единичного момента в зоне сопряжения учитывают формулы (243) для цилиндрического архитрава и формулы (245) для подштамповой плиты. Запишем окончательные значения функций Z,.
Для цилиндрического архитрава:
|
£ |
Z, |
Zz |
Z, |
24 |
|
0,5 |
—704,4 — 1.086 - Д - 3 г0 |
2335 + 17,33 - Д - '0 |
- 1238 — 8.637 - Д - '0 |
2213 + 14,98 -^- 'О |
|
— 0,5 |
1934 + 27,19 -^- '0 |
— 3944 — 50,46 — '0 |
— 2270 — 29,50 '0 |
3874 + 50,26 Г'о |
|
(249) |
|
І | |
2г |
Za |
1 Z, |
|
|
0.226 |
— 1034 + 28 ,С9 |
31770 — 123,2 — |
- 27750 + 100,2 '0 |
46700— 168,7 '0 |
|
-0,226 |
8945 — 3,350 -^- —38020 + 103,0 1—30910 + 89.95 —- 52040 — 151.3 -^- ,.3 | ..з | л 'о | г0 1 г0 1 г0 |
|||
|
Для подштамповой плиты: |
|
(250) |
Величину а определим из условий сопряжения, приравняв в сопряжении моменты производных от функций иг.
Ввиду того, что расчет производится с точностью до первого момента, в зоне сопряжения приравниваются средние значения производных вертикального перемещения uz
TOC \o "1-3" \h \z 0,3 79 1
Гоц J uzed<ie == Л0н J u'ZHclQH. (251)
О 0
Подставив в уравнение (251) выражение иг по формулам (226), перепишем его в виде
Г, щ № [Ді (0,379) - jRi (0)] + Z? \R2 (0,379) - R2 (0)]} =
= r„n [Zn3 [/Ml) - Ri (0)] + Z? [R2 (1) ~~ R2 (0)]}. (252)
Значения Rt и R2 возьмем из табл. 30. Значения функций Z< подставим для цилиндрического архитрава из (249) при £ =—0,5, для подштамповой плиты из (250) при £ = 0,226. В результате получим линейное уравнение для определения неизвестного момента а в сопряжении. Решив его, получим а = 4810 тм. При расчете цилиндрического архитрава к моменту от контактных напряжений в сопряжении следует прибавить момент от внешней нагрузки М„ = 70,2го т/м2.
17* ■ 259
Суммарный момент при £ = —0,5
(w1 +70'2) г°3 = 84'2г°3 т/м°~-
Цилиндрический архитрав рассчитывается при следующих граничных условиях:
І
£ = 0,5 rl jazQ2dQ — 23,29ло т/м2;
О
І
Го I ТrzQdQ = 0;
О
1 1 .
£ = — 0,5 rl\ozQdo 84,2го m/л*2; ft orfo - 0.
0 о
Граничные условия для подштамповой плиты будут
1 і
£ = 0,226 r3on J аЛ = 259г03 т/м2; г02 (' xodq = 0,
О о
І і
£ = - 0,226 , rl J оА - 308, б/-3 т/м2; r\ f то dQ - 0.
О о
Для определения произвольных постоянных, входящих в функции Zit воспользуемся выполненным уже расчетом цилиндрического архитрава и подштамповой плиты на единичный момент а. Произвольные постоянные при действии на цилиндрический архитрав единичного момента на верхнем торце (£ = 0,5) определены ранее. При действии единичного момента на нижнем торце (С = = —0,5) произвольные постоянные С2 и С3 меняют знаки на обратные. Подставив в выражения (241) вместо величины а сначала — Го-23,29 т/м2, затем го -84,2 т/м2 и сложив результаты с учетом сделанного выше замечания относительно знаков, получим окончательные значения произвольных постоянных для цилиндрического архитрава:
Ct = — 186 т/м2, С2 = — 1955 т/м2, С8 =-- 867 т/мг; С4 -_- 650 т/м2.
При вычислении произвольных постоянных для подштамповой плиты воспользуемся выражениями (244):
С1 = — 3860 т/м2; С2 5260 т/м2;
С3 --= 6180 т/м2; С4 - 7120 т/м2
Имея произвольные постоянные, по формулам (227) найдем значения функций Zt при любом как для цилиндрического архи - 260 трава, так и для подштамповой плиты. Значения функций Z,- приведены в табл. 41 и 42. Графики функций показаны на фиг. 44.
|
Таблица 41 Значения функций Z, цилиндрического архитрава (т/м2)
|
|
Таблица 42 Значения функций Z,- подштамповой плиты (т/м2)
|
Дальнейший расчет производим по формулам (226) при п = 1. Формулы (226) будут теперь содержать все известные функции, и определить перемещение и напряжение в любой точке цилиндрического архитрава или подштамповой плиты не представляет затруднений. Ниже приводятся таблицы величин напряжений и перемещений в различных точках цилиндрического архитрава и подштамповой плиты. Эпюры показаны на фиг. 45 и 46.
Интересно отметить, что подштамповая железобетонная плита очень мало снижает момент, действующий на цилиндрический архитрав. Если приложить нагрузку без подштамповой плиты прямо к цилиндрическому архитраву, то момент от нее будет Mq = — 87,2ло т/м2 вместо 84,2г® т/м2 по проделанному расчету. Разница составляет всего 3,6%. Следовательно, при данных соотношениях размеров цилиндрического архитрава и подштамповой плиты сначала можно рассчитать цилиндрический архитрав на внешнюю нагрузку, исходя из предположения, что жесткость подштамповой плиты равна нулю, а затем рассчитать подштампо - вую плиту. При расчете подштамповой плиты граничные условия
Г
|
Я о |
На торцах будут смешанные. По нижнему торцу будет задан момент от внешней нагрузки, по верхнему торцу — перемещения иг, при которых форма поверхности подштамповой плиты в зоне сопряжения! будет совпадать с формой поверхности цилиндрического архитрава.
Напряжения о2 цилиндрического архитрава (в т/м2):
|
О \ |
0,5 |
0,4 |
0,3 |
0,226 |
0,1 |
0 |
0,1 |
-0,226 |
-0,3 |
-0,4 |
-0,5 |
|
0 j —389 |
-317' |
-339 |
—406 |
—593 |
—769 |
—945 |
— 1079 |
— 1193 |
— 1180 |
— 1052 |
|
|
0,2 |
—300 |
—259 |
—298 |
—373 |
-557 |
-730 |
—S05 |
— 1099 |
— 1173 |
-1196 |
— 1088 |
|
0,4 |
-127 |
-145 |
-217 |
—295 |
—500 | —614 |
-771 |
—С64 |
— 1059 |
-1153 |
— 1185 |
|
|
0,6 |
-50 |
— 123 |
— 195 |
—249 |
—380 |
—429 |
-517 |
—643 |
-742 |
—840 |
—969 |
|
0,8 |
—332 |
—352 |
—343 |
—321 |
—262 |
—207 |
— 151 |
—90 |
70 |
—70 |
— 117 |
|
1,0 |
— 1068 |
—897 |
—708 |
—554 |
—265 |
-75 |
245 |
606 |
823 |
1060 |
— 1416 |
|
Перемещения иг подштамповой плиты (в мм):
|
|
Перемещения иг цилиндрического архитрава (в мм):
|
Для сравнения приведем расчет сопряжения цилиндрического архитрава со стальной подштамповой плитой, имеющей те же размеры, что и железобетонная.
Параметры стальной подштамповой плиты
V = 0,30; Ес = 20-106 т/м2. Схема нагружения остается прежней.
Действительная часть и коэффициент при мнимой части корня первого однородного решения для стального цилиндра будут:
А = 2,722; 6= 1,362.
Соответственно изменяются значения гйперболо-тригономе - трических функций:
У = 0,1984; б = 0,6240; К = 3621; ц = 1,139.
Приведем окончательные значения функций Z; для стальной подштамповой плиты.
|
Г ъ |
Z, |
Zt |
||
|
0,226 |
130 Н 25,36 — 'о |
27040— 110,2 Г0 |
—21400 +79,1 4- 'о |
40800— -150,8 4 'о |
|
—0,226 |
7826 - f 0,42 4- 'о |
—34010 + 87,63 4 '0 |
-24410+ 69,36 Д- ГЗ г0 |
46540— —132.2 4; 'о |
|
(253) |
Величину а определим из уравнения (252), правую часть которого умножим на соотношение модулей упругости и коэффициентов Пуассона для бетона и стали, равное
|
К |
|
0,226. |
|
1,15-20-Юв |
(l+vc)Ј6 1,30-4.108
(1 + V6 )Ес
Решив уравнение, получим а = 2798.
Подставив найденное значение а в (249) и (253), вычислим окончательные значения функций ZЈ для цилиндрического архитрава и стальной подштамповой плиты.
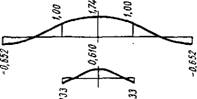
|
Фиг. 47. Вертикальные перемещения железобетонного цилиндрического архитрава и стальной подштамповой плиты в зоне сопряжения. |
Цилиндрический архитрав:
|
S | г, |
^3 |
7 |
||
|
0,5 |
—713,2 |
2527 |
—1358 |
—2335 |
|
—0,5 |
2156 |
—4356 |
—2510 |
4284 |
|
Стальная плита:
|
Имея значения функций Zh нетрудно вычислить напряжения и перемещения железобетонного архитрава и стальной подштам - 264
повой плиты в зоне сопряжения от самоуравновешенной нагрузки.
Эпюры вертикальных перемещений цилиндрического архитрава и стальной подштамповой плиты в зоне сопряжения показаны на фиг. 47.