ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ
ПРИМЕНЕНИЕ ВАРИАЦИОННЫХ МЕТОДОВ К РАСЧЕТУ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ ПРЕССОВ
В статье рассмотрены задачи о расчете плоского элемента, имеющего форму кругового сектора, загруженного краевыми нагрузками, и сплошного кругового цилиндра, загруженного осесим - метричной нагрузкой. Эти задачи имеют между собой некоторое сходство, поэтому для их решения применен единый метод.
Решение задач проведено приближенным способом на основе вариационного принципа Кастильяно, разработанного применительно к рассматриваемому классу задач Тимошенко С. П. [16], Папковичем П. Ф. [1], Филоненко-Бородичом М. М. [3], [4].
Вариационный метод расчета сплошных и полых цилиндров с использованием уравнения Кастильяно подробно разработан Бидерманом В. Л. В статье сделана попытка подобрать такие функции напряжений, которые удовлетворяли бы однородным статическим условиям на торцах при загружении боковой поверхности цилиндра и, наоборот,:
Ставя своей целью проиллюстрировать метод, мы не стремились достигнуть большой точности результатов. расчета. и. ограничились только первыми приближениями. Однако, как показано в работе, даже первые приближения для основных группы усилий дают вполне "удовлетворительные результаты/ - ~ - ~
Плоская задача секториального профиля
|
(1) |
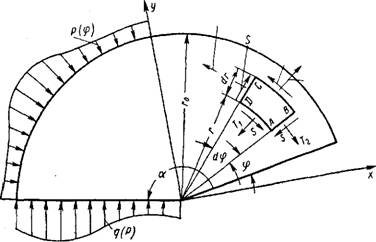
Основные уравнения и подбор функции напряжений. Рассматривая условия равновесия элемента ABCD (фиг. 1), получим уравнения
J. ,._?.S. 0.
R дер ' дг ' г...
Положительные направления усилий и координат показаны на фиг. 1.
Если компоненты усилий выразить через функцию напряжения Эйри при помощи формул
TOC \o "1-3" \h \z г —_L UL. т д2р
1 1 ~ г2 ' 0фа + г ' дг ' дг2
|
• (2) |
„ _______ 1 d2F, J_ dF_
Г дг-оф г2 йф '
То уравнения равновесия (1) будут удовлетворяться при произвольном выборе функции F (г, ф). Однако произвол в выборе
|
Фиг. 1. К выводу уравнений равновесия в полярной системе координат. |
|
Чу м ildr 5 + Гг ИТ г Г)' дг |
F (г, ф) ограничивается подчинением последней условию совместности деформаций.
|
(3) |
Будем искать решение системы уравнений (1) в виде
Ті = Ті + ТІ Т2 - ТІ + Т%,
|
(4) |
|
Є |
S = s° + sK,
Где Ті, Тг, 5° — решения, дающие нулевые значения на контуре; Ті, Т$, SK — решения неоднородной системы уравнений, удовлетворяющие только заданным контурным условиям. Введем безразмерную координату
й перепишем выражения (2) в новой независимой переменной
Г____ d*F 1 dF
;і"г02е2'йфа + r*Q ' dQ '
TOC \o "1-3" \h \z 5==_____ 1 d2F. 1 dF (5)
Функцию напряжений представим также в виде двух слагаемых
F(Q, ср) = Ле. ф) + ^(Є - Ф). (6)
Каждое из которых будем рассматривать в виде
Р(е, Ф) = 2аиАт(е)Фт(<р); (7)
FK(Q, = (е)Фк(ф). (8)
Где т, п = 1,2,3,..., amrt — параметры, подлежащие определению.
|
R __ 1 d2F rl ee«' |
Подставляя І70 из уравнения (7) в выражение (5) и требуя выполнения нулевых значений на контуре, т. е.
R,
От Фоп) = 0
Ф = 0. »
Ф = а
Є-0, е = 1
|
6=0 6 = 1' |
|
1 11 = — Г0 |
|
(9) (10) (П) |
|
" ^^ amnRom®on — 0 |
|
Т-,0 I 2 : |
|
R„ |
|
Rom лтп I „2 |
|
Фоп=0 |
Нетрудно подобрать функции Rom и Ф0„, удовлетворяющие условиям (10).
Примем, например,
, ,\2 3m
|
(12) (13) |
|
Ro |
(е —І) е ;
Отсюда функция F° (q, ф) может быть представлена в виде
Ґ (д, ф) = 2 amnRomOon - 2 атп (q - I)2 е3т (а - ф)2 <?2п, (14)
Где т, п = 1, 2, 3, ...
Подставляя в выражения (5) значения FK (q, ф) из (8), получим
|
R |
|
1 |
|
(15) (16) |
|
Ті = |
|
(17) 317 |
RK
,2 \ Q* 1 Q
Rk RK
Функций RK (0) и Фк (ф), как указывалось ьыше, удовлетворяют только контурным условиям и, следовательно, для каждого частного вида нагружения подбираются самостоятельно.
Рассмотрим случаи загружения по контуру. При этом примем, что нагрузка симметрична относительно оси ординат (фиг. 2, а и б). При q = 1
TOC \o "1-3" \h \z 7? = - р(<р); (18)
= 0, (19)
А при ф = 0 и Ф = а
71 = -<7 (Q); (20)
SK = 0. (21)
Из уравнений (15) и (16), учитывая соответственно условия (18) и (19), получаем
ЯИ1)Фк + /М1)Ф«--гор(ф); • (22) [fl«(l)-/Ml)]<& = 0. (23)
Положив в условии (23) Фк=0, из формулы (22) находим, что
Г2
Фк =--------- Л - р (<Р) = const. (24)
RKW
Из уравнения (16) получаем
= \^(Q)dQdQ. (25)
Таким образом, при равенстве нулю сдвигающих усилий по всему контуру, нагрузка по криволинейной части контура может быть только постоянной. Уравновешивающая ее нагрузка, распределенная на прямолинейной части контура, может быть задана произвольно. И затем, как видно из уравнений (15)—(17) при R = = R (q) и при Ф = Ф (ф) следует, что для подбора R и Ф весь контур должен быть нагружен.
Если же самоуравновешенная нагрузка распределена только на прямолинейной части контура, а сдвигающие усилия по всему контуру равны нулю, можно положить, что
Фк (ф) = const = 1,
Ті е., что
FK = R(Q). (26)
Выражения (15)—(17) примут вид
T1 = \R'k-, (27)
'о
71 = 4^; (28)
Г1
SK = 0. (29)
|
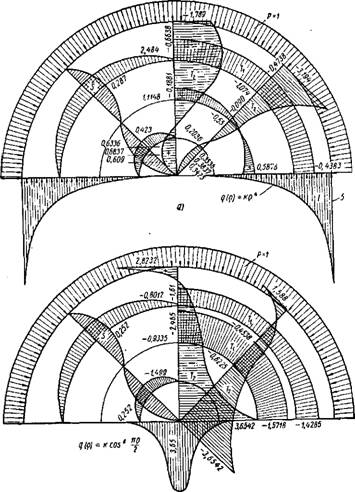
Фиг. 2. Эрюры усилий в полудиске при равномерно распределенной нагрузке по криволинейному контуру и нагрузке, распределенной по прямолинейной части контура: |
|
6) |
А — по закону (q) = kq4; б —по закону q (q) = к cos» Щ - (где к определяется нз условия равновесия системы).
Положим, например, что прямолинейная часть контура нагружена нормальной самоуравновешенной нагрузкой
Q (q) — (/„costcq, (ЗО-)
Т. е., что
Тк2 = -\RK = ^осоэяд; (31)
Го
Отсюда находим, что
' 1 2
RK = — qoro sin яд; (32)
RK = — cos n6 • (33)
Подставляя RK из выражения (32) в формулу (27),' нетрудно убедиться, что криволинейный контур свободен от нагрузки.
Самоуравновешенная нагрузка, распределенная на прямолинейном контуре вида
?(е) = ?о(5е4-1). (34)
Также обеспечивает криволинейный контур незагруженным. В этом легко убедиться, проделав изложенные выше выкладки.
Уравнения равновесия (1) также будут удовлетворяться, если выразить усилия Ті, Г2 и S с помощью функции напряжения Ф = ф (б. ф); по таким формулам
~ г аТ^дф + к >
«—Д.- <37>
Как и прежде, будем полагать, что
Ф) = - Р(в)®(ф). (38)
Введя новую переменную q и учитывая выражения (38), формулы (35)—(37) перепишем в виде
7\ = (я©'" + 2Рв' + J qP" dQ) ; (39)
; T, = ^(qP" + 2P')-, (40)
I о
5 = — — Р'в". (41)
Rt>
Полагая, что Pom = Rom и воп = Ф0;1 [см. формулы (12) и (13) ], рассмотрим здесь только функции Рк и ©к, т. е. функции, 320
удовлетворяющие контурным условиям. Примем при этом, что самоуравновешенной нормальной контурной нагрузкой нагружен только криволинейный контур. Сдвигающие усилия SK по всему контуру равны нулю. В этом случае можно положить Рк= const = = 1, т. е., что
¥К = ©К(Ф). (42)
Отсюда выражения (,39)—(41) примут вид
Тг = 01 ф=о 0 | q = 1, Ф = 0, ф = а. (43)
<р=а
Пусть по криволинейной части контура профиля распределена самоуравновешенная нормальная нагрузка
Р =~ Р (ф). (44)
Т. е., что
П=-^(©; + 2©;) = р(ф). (45)
'о
Отсюда ©к (ф) определится как частный интеграл неоднородного дифференциального уравнения
©«+2©; = р(ф). (46)
Таким образом, функция напряжений F (q, ф) позволяет удовлетворить контурным условиям, когда криволинейная часть контура нагружена постоянной нагрузкой или вовсе ненагружена. Прямолинейную же часть контура возможно нагрузить произвольной нагрузкой.
С помощью функции ^ (q, ф) есть возможность нагрузить криволинейный контур произвольной нагрузкой.
Отсюда путем наложения напряжений, определенных с помощью функций F (е, ф) и ^ (q, ф), можно получить ряд решений задачи при различных распределениях нагрузки по контуру профиля.
Уравнение Кастильяно. Выпишем значения усилий 7\, Т2, S, выражая их, например, через функцию F (q, ф):
|
(47) |
TI = jr 2а™ + ф") +
Т2 — - у 2 AmnRom®o
1 v п \ ^от і ф' j чк
Тт^М"?----------- г)Фоп + 3 '
Эти усилия подобраны так, что удовлетворяют уравнениям равновесия (1) и граничным условиям, но не удовлетворяют
21 Сборник 1835 321
уравнениям совместности деформаций. Для удовлетворения последним воспользуемся вариационным уравнением Кастильяно
V = ~2ШГ 11 + — 2v7\T2 + 2(1 — v) S2]r-dr-d(f>, (48)
Где Е — модуль упругости; v — коэффициент Пуассона; h — толщина профиля.
Усилия, удовлетворяющие и уравнениям равновесия и уравнениям неразрывности деформации, реализуют минимум V. Внося значения Тъ Т2, S из уравнений (47) в условие
|
Rk |
|
Фк R, |
Е; і.
|
(54) |
|
'О |
Нетрудно убедиться, что правая часть выражения (52) равна нулю; отсюда и а = 0. Напряженное состояние профиля опишется формулами
1 Rk
Ф
Г0
|
4-я>к=4-| Ч> 'о S = 0. |
|
(55) (56) |
|
-р'о =-р; |
Пример 2. Рассмотрим случай загружения, когда по криволинейной части контура приложена постоянная равномерно распределенная нагрузка, а по прямолинейной — уравновешивающая ее нагрузка, распределенная по параболе четвертой степени (фиг. 2, а), т. е.
Фк = —рлд = const;
Ф;=Ф;=о;
Коэффициент k определим из условия равновесия
|
1 |
1
|
K — —5 р. |
—р — k | Q* dQ
Откуда 21*
Таким образом,
Q (е) = —5р Q4; ЈK = 5jjY. rfe. rfe; RK = 5jQ4rfg = Q5; ^ = 5Є4.
Вычислив для рассматриваемого случая правую часть уравнения (52), получим
|
(57) |
—0,38094-0,0333я5р^.
Отсюда [см. формулу (53)]
0,38094-О, ОЗЗЗя6 , . _, а = 0,0474939л5 рГо = °'2637^' о,
И напряженное состояние профиля опишется следующими формулами:
Ф і і ф" і
|
К |
|
R„ |
|
Ф |
О ' П2 к '
= р (0,2637q (q - 1) [2 (Q - 1) (я2 — бяф + 6ф2) + (5е — 3) (я - Ф)2 ф2] - е4};
(58)
Т2 = 4" ИоФ0 + = Р [0,5274q (10е2 _ 12q + 3) (я - Ф)2 Ф2 - 5е4];
(59)
|
Rn |
|
Ro |
Ф0 =
-р [1,0548е (е — 1) (2q — 1) ф (я — ф) (я — 2ф)].
Распределение напряжений показано на рис. 2, а, где'принято р = 1. Пример 3. Криволинейная часть контура нагружена постоянной равномерно распределенной нагрузкой, а прямолинейная — уравновешивающей нагрузкой, распределенной по закону (см. фиг. 2, б)
|
Яд _ |
|
35 128 |
|
Р; |
' + cos яд \ 4
Q (q) = k cos8
Коэффициент k, как и прежде, определим из условия равновесия і
Р = k J cos8 dq
Следовательно,
128
|
(60) |
35
|
Яд |
128 f g яе, 8 / 35 8 .
K = ~35~~ J 008 "rrfe = "35-^6 + —з. пяе
+ 1ЇГ sin 2ле - sinS яе + - Щ-sin 4яе);
128 8 л£> 8 /", , . _ 2 |j3 , 4 \
/?к = —gg - COS —= - gg - (1+4 COS яе + 6 cos + 4 cos яе - t - cos яе) =
G
= - gg-(l - f cosng)4;
Фк остается прежней (см. примеры 1 и 2).
Выполняя аналогичные вычисления [(только правой части уравнения (52)], получим
0,0333-3,26676лэ 2 0,1087 2 „,„„ 2 ,,,,
0 = - 0,0474939л5 ^ = "^Г ^ = 0-2319рло. (61)
Усилия определятся по формулам Тг = р |o,2319q (е - 1) [2 (е — 1) (я2 -- бяф + бф2) + (5q - 3) (я - ф)2 ф2j —
8 / 35 I 8 ■ , 7 ■ О 4 9 1 ■ А \)
~ Ж [т + ^5Ш Яе +5Ш 2яе - w5Ш е + "^ёsm е Л;
(62)
Г2 = р |"o,4638g (IOq2 — 12е + 3) (я — ф)2ф2 _ — (1 + cos ne)4J ; (63) S ■= —р [0,4638-2q (є — 1) (2q — 1) ф (я — ф) (я — 2<р)]. (64)
Распределение напряжений в профиле показано на фиг. 2, б, где принято р = 1.
1. Усилия Ту и Т2 с достаточной точностью могут определяться по приведенным формулам, т. е. в первом приближении; что касается сдвигающего усилия S, то потребуется, очевидно, взять второе приближение.
2. Приведенным в статье методом возможно рассчитывать профили, мало отклоняющиеся от круга, например очерченные по параболе четвертой степени.