ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ
Предложения по расчету несущей способности толстых железобетонных плит с напрягаемой арматурой
Ввиду пространственной формы, наличия бокового давления обоймы (являющейся функцией нагрузки) и других особенностей конструкции напряженное состояние, возникающее в момент разрушения плиты, охарактеризовать теоретически, с помощью положений сопротивления материалов или теории упругости, не представляется возможным.
В данном случае проще всего определить несущую способность конструкции, пользуясь методом предельного равновесия, предложенным Гвоздевым А. А. Согласно этому методу несущая способность может быть найдена как наибольшее усилие, удовлетворяющее условиям равновесия и предельным условиям состояния конструкции.
При рассмотрении напряженного состояния круглых толстых плит началом разрушения можно считать этап, на котором деформации еще достаточно малы, что позволяет пренебречь изменениями геометрических размеров образца. При достижении разрушающей нагрузки деформации конструкции возрастают без повышения усилия. 29$
В данном случае толстую цилиндрическую плиту можно рассматривать как элемент, нагруженный центрально приложенной нагрузкой и работающий на сжатие.
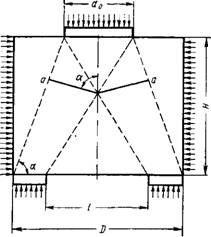
Предельное состояние бетона возникает в сечении а—а (фиг. 20), расположение и площадь которого зависят от геометрических размеров образца и штампа.
Условие равновесия в таком случае имеет вид
Рвн = °б/ sin а,
Где аб — сопротивление бетона; f—площадь рабочей поверхности; а — угол наклона внутреннего усилия коси z.
|
Фиг. 20. Схема распределения главных сжимающих напряжений в толстой цилиндрической плите, принятая для расчета. |
На основании опытных данных считаем, что разрушение бетона происходит в области II (см. фиг. 16) по некоторой поверхности, площадь которой равна fK. Для простоты принята схема напряженного состояния образца перед разрушением (фиг. 20).
Разрушающая нагрузка Рразр при этих условиях определяется из уравнения равновесия
Рразр = [o6]fK sin а; (1)
Здесь [об] — величина предельного сопротивления бетона на поверхности а — а в условиях объемного неравномерного сжатия. Площадь fK поверхности а — а может быть представлена в виде
|
Я di |
|
H |
(Ш)Si"8 а = (тті-)2 sin2а'
Где
Я di
Для определения а пользуемся формулой
2 Н
Tga =
D — d о
Величина сопротивления бетона [об] на поверхности а—а определена на основании результатов исрытания образцов серий ВП и КПО.
Виях всестороннего неравномерного сжатия при ох = сг2 = = <7<>; °з > Qi - Как известно, условие прочности бетона в этом случае имеет вид
0б = о3 = R"np + 4 о0, (2)
И разрушающая нагрузка определяется выражением
|
Разр |
Я/Я
(RnP + 4о0)
Где 03 — удельное давление под штампом; Rnp — предельная прочность бетона; о0 — величина бокового давления на бетон. При изменении соотношений о1, о2 и о3, а также величин D/d0 и 1/D условие (2) видоизменяется (фиг. 21).
|
Рравр = a (Rnp + bq) fu |
|
(3) |
|
Или, в общем виде, 300 |
По результатам испытания образцов серий ВП и КПО получена зависимость между Рразр, Rnp и q:
1 разр
Приравнивая правые части выражений (1) и (3), найдем a6fK sin а = a (RnP + bq) fMm или, подставляя значения fK и сокращая fmm, получим
|
2 Sin4 а |
__ °{КР + ья)
\ l + d0 )
Таким образом, условие прочности бетона в сечении а — а зависит от соотношений геометрических размеров образца, диаметров штампа и кольца.
Анализируя результаты испытаний всех образцов (серий ВП, КПО и КПБ) и используя выражения (2) и (4), получили следующую эмпирическую формулу для определения нагрузки, разрушающей образцы:
Рраэр = [Rnp + 4oJ 0,175nd0D Sin4 аг]тр, (5)
Н
Где о0 = \ ,2-jyq\
Х\тр — коэффициент, учитывающий влияние трения на поверхностях образца;
Л тр — н
Условием применения формулы является равенство
F шт ^ Рк >
Где Fк — площадь опорного кольца.
Для проверки правильности принятых предпосылок вычислены значения Рразр для плит, размеры которых соответствуют образцам серии КПБ. По результатам вычислений построены теоретические графики зависимости величины разрушающей нагрузки
От высоты плиты и диаметра штампа при - g-= 0,6 (фиг. 22, а).
Получено хорошее согласование результатов опыта и значений, вычисленных по формуле (5).
При одинаковой высоте плиты разрушающая нагрузка резко
Снижается при изменении отношения от 1 до 2. При увели-
И q
D г
Чении - г - до 5 разрушающая нагрузка снижается менее интен-
UQ
Сивно. С увеличением высоты плиты характер изменения Рраэр остается неизменным, но абсолютное значение^ разрушающей нагрузки повышается. ^
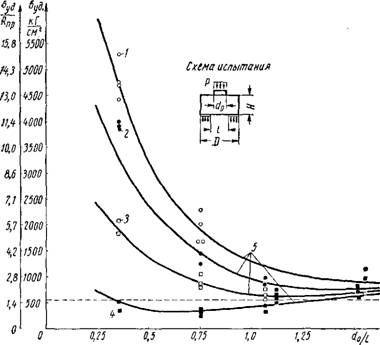
Представляется интересным проследить, в каких пределах изменяется величина удельного давления п(Тд штампом оуэ (фиг. 22, б).
1-4 — опытные данные при: *L =0,8 (/); 0,6 (2); 0,4 (3) и = 0 ,2
|
Фиг. 22. Сравнение теоретических и опытных значений разрушающей нагрузки (а) и удельного давления под штампом (б) при разрушении: |
|
В) |
(4); 5—теоретические графики.
При постоянных прочности бетона Rnp и увёлйчёйий предварительного напряжения а среднее удельное давление при разру-
Do, Н
Шении зависит от диаметра штампа и высоты образца
Для образца серии КПБ (q = 60 кГ/см2, R ^ 500 кГ/см2 и I — 0.55D) характер графика оуд, ~ изменяется в зависимо-
Н
Сти от высоты плиты. При = 0,2 величина ауд составляла примерно 2Rnp для = 0,25 и --=1,5. Для промежуточных значений предельное давление под штампом снизилось
До 0^5 = Rip. н
При = 0,8 величина удельного давления под штампом
При малых диаметрах штампа достигала 14—15 Rnp. С увеличением диаметра штампа эта величина снижается и стремится к некоторому значению, которое может быть вычислено по формуле (5), полагая в ней d0 = D и sin а = 1:
Оуд = 1.43 (Rnp + 4а0) х]тр.
Это значение для образцов серии КПБ изменяется от 530 до 570 кГ/см2 и в среднем может быть примерно равным 550 кГ/см2 (1,5Rnp).