ПОЛУПРОВОДНИКОВЫЙ ЭЛЕКТРОПРИВОД
ЗАМКНУТЫЕ СИСТЕМЫ УПРАВЛЕНИЯ АСИНХРОННЫМИ ЭЛЕКТРОПРИВОДАМИ С ПОЛУПРОВОДНИКОВЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
4.1. ДИНАМИЧЕСКИЕ СВОЙСТВА АСИНХРОННОГО ДВИГАТЕЛЯ ПРИ РАЗЛИЧНЫХ СПОСОБАХ ПАРАМЕТРИЧЕСКОГО УПРАВЛЕНИЯ
Как показано в ряде работ [6, 76—78, 83, 84], при применении замкнутых САУ удается значительно расширить функциональные возможности асинхронных электроприводов с полупроводниковыми преобразователями и обеспечить качественно новые свойства систем параметрического управления асинхронными двигателями. Используя в зависимости от технических требований различные виды обратных связей — по скорости; положению, току ротора (для двигателей с контактными кольцами) и статора, можно реализовать управляемые пускотормозные режимы, плавное регулирование скорости в широких пределах, позиционирование производственных механизмов и т. д.
Для обеспечения требуемого качества замкнутых САУ в переходных и установившихся режимах необходимо располагать обоснованными методами анализа и синтеза таких систем, основанными на изучении динамических свойств элементов, входящих в САУ, и, в первую очередь, методами исследования асинхронного двигателя как объекта регулирования.
Так как при управлении от полупроводниковых преобразователей осуществляется импульсное воздействие на асинхронный двигатель, то момент асинхронного двигателя даже при установившейся скорости имеет пульсирующий характер и содержит гладкую и переменную составляющие. Частота пульсаций последней (fn) зависит от схемы преобразователя. В рациональных схемах преобразователей, включаемых в статорные цепи для регулирования переменного напряжения (см. рис. 1.1,а; 1.2,6), /п^300 Гц при fo—50 Гц; в преобразователях, предназначенных для реализации режима динамического торможения (см. рис. 1.8,в, г), /п^ЮО Гц при fo=50 Гц и в преобразователях для импульсного управления в роторных цепях (см. рис. 1.5,a) fn^ЗОО-МЮО Гц. Очевидно, указанные значения fn значительно выше реально достижимой полосы пропускания (fnp) непрерывной части системы автоматического управления, так что всегда выполняется условие
fn>3fnp, (4.1)
позволяющее свести импульсное звено к непрерывному [79], т. е. пульсирующая составляющая момента не может оказать сколько - нибудь заметного влияния на динамические показатели САУ. В свя
зи с этим полупроводниковые преобразователи можно рассматривать как непрерывное звено, на выходе которого регулируется полезная составляющая управляющего воздействия, определяющая постоянную (среднюю) составляющую момента асинхронного двигателя. Укажем, что возможность рассмотрения систем с полупроводниковыми преобразователями путем выделения непрерывной полезной составляющей обоснована в [80].
В системах параметрического управления необходимо исследовать частотные характеристики асинхронного двигателя при следующих способах воздействия:
1) регулировании первой гармоники переменного напряжения (РПН), прикладываемого к статорным цепям двигателя. В этом случае изменяются действующее значение (Vі*) и амплитуда (Um) основной гармоники;
2) регулировании выпрямленного (постоянного) напряжения (РВН), когда изменяется значение Un в режиме динамического торможения;
3) регулировании добавочного сопротивления (РДС) в роторе асинхронного двигателя с контактными кольцами.
Вначале исследуем динамические характеристики асинхронного двигателя при его упрощенном описании без учета электромагнитных переходных процессов; такой подход используется в ряде работ [81, 83, 85].
Выражения (3.36), (3.61) позволяют определить установившийся момент асинхронных короткозамкнутых двигателей. Для двигателей с контактными кольцами способы управления, связанные с регулированием переменного или постоянного напряжения, могут быть реализованы при введении добавочных невыключаемых сопротивлений в роторную цепь (і?2д) • Кроме того, может быть осуществлено регулирование R? д. В этих случаях изменяется суммарное активное сопротивление роторной цепи ^22==^2+^2д - Для удобства дальнейшего рассмотрения целесообразно ввести безразмерный коэффициент r = /?22/i?2= (#2 + #2д)/#2 [81]. ОчЄВИДНО, для короткозамкнутых двигателей г— 1, при использовании способов управления РПН и РВН для двигателей с контактными кольцами г>1, r=const, при реализации способа РДС г^1, r=var. При включении добавочных сопротивлений изменяются коэффициенты затухания роторного контура arz=R'22,/Xr и a'rx = R,2z/cXr по сравнению с аналогичными величинами для короткозамкнутого ротора (ar=R'ъ/Хг и a'r=Rf2lоХг), однако при введении коэффициента г они связаны простой зависимостью: а'гл — агг, arz=arr. С учетом этого запишем выражения для установившегося момента асинхронного двигателя при различных способах параметрического управления:
РПН
|
(4.2) |
т _ _____________ Um2_ (1 — a)a/rs________________ Uт2 (Г — о)ar'rs
aXs [(а/а/ro — s)2 -f (а/r+а/ ,s)a] as Xs (a2 + b2)
где a=a'sa'rrc—s; fc = a/rr+!a'ss;
рдс, когда к статору приложено номинальное напряжение сети (Um= 1)
(і—к»» 43
сХ5(а* + !>«) ’
РВН
т = ~ ^°а(17 °)“Л -------------------- .------------------ (4.4)
За/ оЛ'у (агг)2+Ю2
Выражения (4.2) — (4.4), являющиеся уравнениями статических механических характеристик асинхронного двигателя, можно привести к форме записи в виде формул Клосса. Так, при регулировании первой гармоники переменного напряжения выражение для момента может быть записано в следующем виде:
щ _ 2mK(l j - е)__________________ 2тк>б(1 -)- e)Um2 ^ ^
s/sk + sK/s - f - 2е s/sK sK/s - f - 2є
где mK — критический момент двигателя на регулировочной характеристике; тК)б — критический момент двигателя на естественной (базовой) характеристике, когда Um= 1; є — конструктивный коэффициент двигателя.
Переходя от (4.2) к (4.5), получаем:
тк =------------ т v................................................. ; (4.6)
[V(*s2+ !)(«/+ !)+«/(!-«)]
s„ = *r'rVi(a; o' +1)/(«/ +1) = arr 1/(0./ + l)/(a/ + 0“); (4.7) . = a/ (1 _ a) / Y(a/ + 1) (a/ + 1). (4.8)
Значение тк, б определяется из (4.6) при подстановке в него Um=. При регулировании добавочного сопротивления в роторе в (4.5) также нужно брать Um= 1.
Для режима динамического торможения формула Клосса записывается в следующем виде:
т=2тк, д>т/ (юк/со+ш/сок) =
= 2тк, б,д, тС/п2/ (юк/со+со/сок), (4.9)
где тк, д>Т, сок — критический момент и скорость в режиме динамического торможения; тк, б.д. т — критический момент динамического торможения на базовой характеристике, когда Un= 1.
Приводя (4.4) к виду (4.9), получаем:
тк, д>т = - ипЦ-о)/ (6Xsas2); (4.10)
coK = a Гг. (4.11)
Значение тК)б, д,т определяется из (4.10) при подстановке в него Un= 1.
116
Для исследования динамических свойств асинхронного двигателя используем также уравнение динамики электропривода
т—mc—JD о. (4.12)
Как видно из (4.2) — (4.4), даже при упрощенном описании асинхронный двигатель является нелинейным объектом, и для анализа частотных характеристик целесообразно воспользоваться методом математической линеаризации нелинейных объектов путем разложения описывающих их уравнений в ряд Тейлора [79], что позволяет, используя теорию линейных САУ, изучить свойства объекта «в малом» при незначительном отклонении переменных от координат центра разложения, соответствующих выбранному установившемуся режиму.
Момент асинхронного двигателя зависит от управляющего воздействия X и скорости (скольжения) двигателя, т. е. m=fi(X, ю). Очевидно, для РПН X=Um, для РДС Х=г, для РВН X=Un.
Точка установившегося режима характеризуется координатами Ху, coy(sy), ту. Придадим приращение АХ управляющему воздействию в окрестности этой точки. Вследствие этого возникает приращение момента Ат и скорости Доз, а также скольжения As. Определим приращение момента асинхронного двигателя, воспользовавшись разложением в ряд Тейлора:
|
л і дт • Д<о-|------- х=ху |
|
АХ = /яу - J - kxAX |
|
х=ху |
|
т — ту -}- Ат = mv-f- у ди> |
— &2Дсо, (4-13)
где k=дт/дХ—коэффициент чувствительности момента двигателя по управляющему воздействию в центре разложения при <o=const; Дсо = 0; k2——дт/дсо — коэффициент жесткости механической характеристики двигателя в центре разложения при Х= =const, АХ=0. Подставим (4.13) в (4.12) и учтем, что в установившемся режиме my = mc, тогда уравнение динамики электропривода, записанное в «малом», примет следующий вид:
Am=kvAX—&2Д<о = /рДсо, (4.14)
что позволяет записать передаточную функцию асинхронного двигателя по управляющему воздействию, принимая в качестве выходной величины приращение скорости Дсо:
Wiy(p) =А(й/АХ=k/(Jp+k2) =kR/ (тм р+1), (4.15)
где kR—ki/k2 — коэффициент передачи (усиления) асинхронного двигателя в установившемся режиме; тм=//&2 — электромеханическая постоянная времени двигателя.
Аналогичным образом может быть получена передаточная функция асинхронного двигателя по возмущающему воздействию,
Рис. 4.1. Структурные схемы асинхронного двигателя в «малом» при упрощенном;
описании:
а — по управляющему воздействию; б — по возмущающему воздействию
т. е. при изменении момента статической нагрузки на Дтс, когда ЛХ = 0:
ТР1в (р) = Д-со/Дтс =
|
(4.16) |
■1 /{Jp + k2) = — 1/^2(ТмР+1).
На рис. 4.1 показаны структурные схемы для рассматриваемых случаев. Выражения для определения ku k2, kA, тм при различных способах параметрического управления приведены в табл. 4.1, где е=а'saVcr-fs; / = a'rr—a'ss.
|
(4.17) |
Как видно из рис. 4.1, передаточная функция асинхронного двигателя по управляющему воздействию представляет собой интегрирующее звено, охваченное внутренней обратной связью по скорости с коэффициентом k2, в прямой канал включено усилительное звено с коэффициентом ky. Анализ выражений для k2, £д, тм показывает, что при s<sK (РПН, РДС) или (d<g>k (РВН) k2>0r тм>0 и двигатель описывается устойчивым апериодическим звеном в соответствии с (4.15). Если же s>sK (РПН и РДС) или о)>сок (РВН), то &2<0, тм<С0 и двигатель представляет собой неустойчивое апериодическое звено
і і р — і
Динамические свойства асинхронного двигателя при рассмотрении в «малом» определяются значениями kA и тм, которые зависят от координат центра разложения (Um и s при РПН, г и s при РДС, Un и со при РВН). При использовании схемы ЗТТ или ШИП регулируемое переменное напряжение изменяется в следующих пределах: Um=6—1. Диапазон изменения Un зависит от выбранной схемы преобразователя. Для схемы двухполупериодного выпрямителя с шунтированием [23]:
|
_ 1/3 |
|
(4.18) |
(l + cosa,).
Минимальное значение ал = 30° и Unmax—1,028, т. е. для этой схемы ип = 0—1,028.
Пределы изменения г для систем РДС зависят от минимального значения момента, который необходимо обеспечить на регулировочных характеристиках, и требуемого диапазона регулирова - 118
|
РПН |
РДС |
РВН |
||||||||||||
|
Um |
5 |
•V |
тм |
г |
S |
Ъ |
V |
СО |
тм |
|||||
|
0,1 |
0,04 |
1,27 |
114 |
0,1 |
1,04 |
—0,1 |
5,2 |
0,1 |
—1,35 |
6,8 |
—11 |
|||
|
0,2 |
0,07 |
3,86 |
217 |
0,2 |
1,65 |
—0,2 |
10 |
0,2 |
—0,93 |
4,7 |
—11 |
|||
|
0,2 |
0,4 |
0,09 |
70 |
3230 |
1,0 |
0,4 |
2,02 |
-0,4 |
231 |
0,2 |
0,4 |
—0,52 |
7,5 |
—32 |
|
0,6 |
0,08 |
—25 |
—1167 |
0,6 |
1,93 |
—0,6 |
—50 |
0,6 |
—0,35 |
10,7 |
—69 |
|||
|
1,0 |
0,07 |
—18 |
—1052 |
1,0 |
1,54 |
-1,0 |
—48 |
1,0 |
—0,21 |
17,5 |
—185 |
|||
|
0,1 |
0,17 |
0,64 |
28 |
0,1 |
0,12 |
—0,01 |
36 |
0,1 |
—5,4 |
3,4 |
—2,8 |
|||
|
0,2 |
0,28 |
1,93 |
54 |
0,2 |
0,24 |
—0,02 |
37 |
0,2 |
—3,7 |
2,3 |
-2,8 |
|||
|
0,4 |
0,4 |
0,34 |
35 |
807 |
10 |
0,4 |
0,47 |
—0,04 |
39 |
0,4 |
0,4 |
—2,1 |
3,7 |
—3,1 |
|
0,6 |
0,33 |
—12 |
—292 |
0,6 |
0,68 |
—0,06 |
43 |
0,6 |
—1,4 |
5,4 |
—17 |
|||
|
1,0 |
0,27 |
—9 |
—263 |
1,0 |
1,04 |
—0,1 |
52 |
1,0 |
—0,85 |
8,8 |
—46 |
|||
|
0,1 |
0,39 |
0,42 |
13 |
0,1 |
0,06 |
—0,005 |
70 |
0,1 |
— 12 |
2,3 |
—1,3 |
|||
|
0,2 |
0,63 |
1,28 |
24 |
0,2 |
0,12 |
—0,01 |
71 |
0,2 |
—8,4 |
1,6 |
-1,3 |
|||
|
0,6 |
0,4 |
0,77 |
24 |
359 |
20 |
0.4 |
0,24 |
—0,02 |
73 |
0,6 |
0,4 |
—4,7 |
2,5 |
—3,6 |
|
0,6 |
0,74 |
—8 |
—130 |
0,6 |
0,36 |
—0,03 |
76 |
0,6 |
-3,2 |
3,6 |
—7,6 |
|||
|
1,0 |
0,60 |
—6 |
-.117 |
1,0 |
0,58 |
—0,05 |
82 |
1,0 |
— Г,9 |
5,8 |
—20 |
|||
|
0,1 |
1,10 |
0,25 |
4,5 |
0,1 |
0,025 |
—0,002 |
173 |
0,1 |
—33 |
1,4 |
—0,45 |
|||
|
0,2 |
1,74 |
0,77 |
8,7 |
0,2 |
0,05 |
—0,004 |
174 |
0,2 |
—23 |
0,9 |
—0,45 |
|||
|
1,0 |
0,4 |
2,14 |
14 |
129 |
50 |
0,4 |
0,1 |
—0,00g |
176 |
1,0 |
0,4 |
—13 |
1,5 |
—1,3 |
|
0,6 |
2,06 |
—4,9 |
—47 |
0,6 |
0,15 |
-0,01? |
178 |
0,6 |
—9 |
2,1 |
—2,7 |
|||
|
1,0 |
1,67 |
—3,6 |
—42 |
1,0 |
0,24 |
—0,02 |
183 |
1,С |
—5,3 |
3,5 |
—7,4 |
ния скорости. Как показывает анализ, практические требования могут быть удовлетворены, если г изменяется от 1 до 50—70.
Для иллюстрации существенного изменения параметров двигателя, определяющих его динамические свойства, в табл. 4.2 для двигателей MTKF111-6 (РПН, РВН) и MTF111-6 (РДС) приведены значения kR и тм при различных координатах центра разложения, а также указан установившийся момент двигателя цу= =My/MN, соответствующий этим координатам. Отрицательные значения тм указывают на то, что звено является неустойчивым и его передаточная функция описывается (4.17).
Таким образом, как показывают предварительные исследования, даже при упрощенном описании (без учета электромагнитных переходных процессов) асинхронный двигатель является нелинейным звеном, динамические свойства которого при рассмотрении в «малом» резко изменяются в зависимости от координат точки установившегося режима.
Для обоснованного синтеза замкнутых САУ необходимо исследовать частотные свойства асинхронного двигателя с учетом электромагнитных переходных процессов. В этом случае двигатель описывается системой нелинейных дифференциальных уравнений, и анализ его динамических показателей может быть также произведен только в «малом» путем математической линеаризации нелинейной системы в окрестности центра разложения. В ряде работ
проведено исследование указанным методом асинхронного двигателя как объекта автоматического регулирования при различных способах параметрического управления [82, 86—92].
Для построения частотных характеристик используем систему дифференциальных уравнений, записанную через переменные ^Ps, При исследовании способов РПН и РДС, когда схема включения машины симметрична, скорость вращения координатных осей может быть выбрана произвольной. Однако целесообразно принять (ок=1, так как в этом случае вектор us неподвижен в пространстве и Us=Um. При (ок=1 система уравнений (3.1) принимает следующий вид:
= (“s' + /) Is - <К Wr+ZWS; )
|
(4.19) |
0 = (а/ г+js) *V - a/ rks%, + DWj.
Она дополняется выражением для момента (3.2) и уравнением динамики электропривода (4.12).
Для режима динамического торможения используем следующую систему дифференциальных уравнений, записанную при (Ок=0 [93]:
|
рг, |
<$s
|
Ш_т jWr Дсо |
|
A Ws AFr |
|
(4.21) |
|
0 = DWar + 0LrrWar + 0 = OTpr — ksar'rWts — «Тт+а/гТрг, j a также уравнения (3.51), (4.12). Установившиеся значения переменных Ч^у, 4Vy, характеризующие работу электропривода в точке с заданными координатами, можно определить для РПН, РДС из (3.9), а для РВН из (3.58). Для отыскания передаточных функций придадим приращения переменным в (4.19), (4.20), разложим эти выражения в ряд Тейлора, отбросим члены более высокого порядка, чем сами отклонения, и вычтем уравнения установившегося режима. В результате получим систему линейных уравнений в приращениях, определяющую динамические свойства асинхронных двигателей в «малом» с учетом электромагнитных переходных процессов при различных способах параметрического управления. Эти уравнения, записанные в операторной форме при нулевых начальных условиях, имеют следующий вид: РПН а/+/+р — KaJ — ksar' г а/ г -{- js--p |
|
(4.20) |
|
РДС
|
|
ах |
|
Amc - |
|
Acj |
|
A(jJ |
|
Am |
|
Am |
|
_1_ _Jp_ щ(р) |
|
1 JP Wz(p) |
|
wi(p) |
|
S) |
|
a-) |
|
as P ^ ^ras' |
A %s |
AUJV3 |
||
|
0 a/r--p co |
AWar |
— |
—ЧГрг Aco |
|
|
— ksa/r —со ar'r--p |
A «V |
F«rAco |
|
Рис. 4.2. Структурные схемы асинхронного двигателя при рассмотрении в «малом» с учетом электромагнитных переходных процессов: а — по управляющему воздействию; б — по возмущающему воздействию |
|
(4.23)# |
|
Выражения для приращения момента имеют вид РПН и РДС |
|
Ш = -*£- Im [(ЧГ, X ЛТГ*) + (AW„ X Wr*)]; (4.24); алв РВН |
|
Am=kr/[War(AWv — -kAWfiг) +ДЧ'а, OFp^-^pr) ] laXs. (4.25) Определим по (4.24) или (4.25) приращение момента, что требует расчета установившихся значений потокосцеплений по (3.9), (3.58) и их приращений по (4.21) — (4.23). Выполнив указанные вычисления, получим Am{p) = Wi (р) АХ— W2 (р) Дсо, (4.26) где Wx(p)=Am(p)/AX(p) — выраженное в операторной форме отношение приращения момента к вызвавшему его приращению управляющего воздействия при co = const, Асо=0; №2(0) = =—Ат(р) /Дсо(р)—выраженное в операторной форме отношение приращения момента к вызвавшему его приращению скорости при Х=const, АХ=0. Как видно из (4.26), приращение момента определяется не только изменением управляющего воздействия, но также зависит от изменения скорости. Эта внутренняя обратная связь по скорости оказывает существенное влияние на динамические свойства асинхронного двигателя. Используя (4.26) и уравнение динамики электропривода, можно получить передаточные функции асинхронного двигателя при его описании с учетом электромагнитных переходных процессов Wx(p) |
|
РВН |
|
г (р) = Mel у Д Х(р) А<й(р) Атс(р) |
|
JP + W2(P) ’ 1 |
|
W2B(p) = |
Структурные схемы для этих случаев приведены на рис. 4.2. Значения W(p) и W2{p) определяются из следующих выражений:
РПН
W (р) = (1~а)аг'гит bp3 + [g(s— l)--bc]p'2 + 2s(ac + bd)p + 2s(a? + b2) гИ) а^(д2_|_62) jp4 _|_ 2ср»-f (c* + 2a + d?)p*+2(bd+ac)p--(a?+b2)’
(4.28)
0^(а24-62)
|
(4.29) |
а/r jP3 4- (а/r с + g — cfc)/?2 + (ЄС + df — ga/r - bs)p+{ae-- bf) p* + 2c/?3+ (c2 + 2a-f d*)p + 2{bd + ac)p + (a2 + 62)
X
где с == а/ - f - а/ r; cf = 1 - f - s;
РДС
(1 -- О - ) а/ s
|
X |
o^(«2 + 62)
|
(4.30) |
|
X |
а/ rp3 + (°/ rc + e — ds)p2 - f (ec + df + aa/ r — bs)p-- (де 4- bf) p4 4- 2cps 4- (C2 4- 2a 4- d2)p2 4- 2(bd + ac)p+ (a* 4- 62)
PBH
|
X |
|
(4.31) |
|
X |
|
(4.32) (4.33) |
|
PZ + K' + «/ г + arr)P2 + [v(2a/ + <*/r) + w2] P 4- a/ f(arr)2 4- CO2] ^7 /„4 _ (1 — a) a/ rUn*__________________ [(arr)3 + a/™> 1 P2 + ^ 2 Зо^а/2 [(arr)2 4- со2]2 p3 4- (a/ 4- a,/r 4- arr)p2 4- 4- {2(1—o)ar, arr2to24-[(afr)2 4- ft>2}[arr(a/-fa/r)—со2]} l+Ky)4—1 4- [arr(2a/ 4- a/r) 4- co2J p 4- 0/ [(arr)2 4- CO2] Выражение (4.27) можно записать в виде многочлена Ц7 /р _________________ ^д(Др3 Ч~ Др2 + А/7 Ч~ 1)________________________ п B1P5+B! P4 + B„Ps + B«f! + B. P+l ■ |
|
I/3aXs a/ [(arr)2 4- a>2] P2 + 2arrp 4- 2 [(arr)2 4- со2]________________ |
|
Kip) |
Значения коэффициентов многочлена для различных способов параметрического управления приведены в табл. 4.3.
Определение полюсов и нулей передаточной функции (4.33) для ряда двигателей показывает, что эта функция может быть представлена совокупностью элементарных звеньев первого и второго порядка, что позволяет записать (4.33) в следующем виде:
|
ІЧР + }) ІЧ2Р2 ±2ЪЧР + 1) |
|
ЧР + 1 (Ч2Р2 + 2Ї4ЧР + 0 (хб2/;2 + %ьЧР + !) |
РПН и РДС
|
Коэффициент |
РПН |
РДС |
PBH |
|
А |
ь 2 s(a2 + b2) |
/ ar г (де + 6f) |
0 |
|
А2 |
a(s— 1) + be 2 s(a2 + b2) |
a'rc +6 — ds ae--bf |
1 2[(arr)2 + <o2J |
|
Аз |
ас + bd a2 + b2 |
ec --df-- aar r — bs ae + bf |
arr (arr)2 + <o2 |
|
Вг |
JoXs(a2 + b2) |
J*Xs{a2 + b2) |
0 Продолжение табл. 4.3 |
|
(1—eJa'rL^ae + bf) |
(1 — e)cx'r(a<?-f6f) |
||
|
Коэффи циент |
РПН |
РДС |
РВН |
|
В, |
2cBi |
2c£i |
3JXso a' [(arr)2 + <08] (1 - aJv’t'jKv)*-»*] |
|
В* |
/ (c.+2e + d»)^ + -^L ae-j-6/ |
/ (ca + 2д + rf3) - f - ~~~r ae--bf |
(a, J-J-a'r + arr)j32 |
|
В< |
б + с о! г — ds 2(ac - f bd)B1 +--------------------------------- 1 ae + bf |
e-j - с air — ds 2(ac + Ы) В, H------------------- —---------- ae--bf |
[arr(2a' + a^r) + <o2] 32 + (arr)5 - f - a' rto2 + , as [(<V)4—*>4] |
|
Въ |
ec - j-df 4- aa'r—bs (a2 I ь-пр I r |
ec + df + aa' r — bs (fA 1 P 1 ' |
, 2(1 — ff)a^arr2a>2 а$[(аГг)а + <°2] B2 + , + as [(arr)4 — w4] arr((x'4-a'r) — w2 as 1Ы)2 — to2] |
|
V'* | U )L>i - J- ae + bf |
a Г & )#1 + . .„ ae + bf |
|
Т а б л и ц а 4.3 |
|
1-0 4* |
ю
сл
|
РПН |
РДС |
|||||||||||||
|
Um |
tl |
Кг |
*4 |
Ї4 |
*5 |
Те |
г |
S |
Ті |
*2 |
||||
|
0.1 |
1,09 |
2,96 |
0,13 |
111 |
1,65 |
0,81 |
1,18 |
0,47 |
0,1 |
2,06 |
1,06 |
|||
|
0.2 |
1.0 |
2,03 |
0,13 |
216 |
1,31 |
0,72 |
1,32 |
0,44 |
0.2 |
2,44 |
1,08 |
|||
|
0.2 |
0.4 |
0,89 |
1,29 |
0,06 |
3333 |
1.0 |
0,73 |
1,34 |
0,23 |
1.0 |
0,4 |
19,3 |
1,12 |
|
|
0.6 |
0,8 |
0.94 |
—0,02 |
—1149 |
0,89 |
0,71 |
1,22 |
0,11 |
0,6 |
— 1,8 |
1,08 |
|||
|
1.0 |
0,71 |
0,6 |
—0,15 |
—1041 |
0,76 |
0,65 |
1,0 |
0,04 |
1.0 |
—0,48 |
0,99 |
|||
|
0.1 |
1,09 |
2,96 |
0,13 |
27 |
1.69 |
0,78 |
1.18 |
0,48 |
0.1 |
0,21 |
1,03 |
|||
|
0.2 |
1.0 |
2,03 |
0,13 |
54 |
1,29 |
0,71 |
1,34 |
0,45 |
0.2 |
0,2 |
1,03 |
|||
|
0.4 |
0.4 |
0,89 |
1,29 |
0,06 |
840 |
1,0 |
0.73 |
1.34 |
0,22 |
10 |
0.4 |
0,2 |
1,03 |
|
|
0.6 |
0,8 |
0,94 |
—0,02 |
—292 |
0,89 |
0,71 |
1,22 |
0,11 |
0.6 |
0,21 |
1,03 |
|||
|
1.0 |
0,71 |
0,6 |
—0,15 |
—262 |
0,76 |
0,65 |
1.0 |
0,04 |
1.0 |
0,22 |
1,03 |
|||
|
0.1 |
1.09 |
2,96 |
0,13 |
11 |
1,75 |
0,74 |
1,18 |
0,5 |
0.1 |
0,11 |
1,01 |
|||
|
0.2 |
1.0 |
2,03 |
0,13 |
24 |
1,26 |
0,68 |
1,38 |
0.45 |
0,2 |
0,11 |
1,01 |
|||
|
0.6 |
0.4 |
0.89 |
1,29 |
0,06 |
381 |
1.0 |
0,72 |
1,34 |
0,22 |
20 |
0,4 |
0,11 |
1,01 |
|
|
0.6 |
0,8 |
0,94 |
—0,02 |
— 131 |
0.88 |
0,71 |
1.21 |
0,11 |
0,6 |
0.11 |
1,01 |
|||
|
1.0 |
0,71 |
0.6 |
—0,15 |
—117 |
0,76 |
0,65 |
1.0 |
0,04 |
1.0 |
0,11 |
1,01 |
|||
|
0.1 |
1,09 |
2,96 |
0,13 |
3,8 |
1,89 |
0.52 |
1.12 |
0,54 |
1.0 |
0,04 |
1,0 |
|||
|
0.2 |
1.0 |
2,03 |
0.13 |
8,8 |
1,15 |
0,64 |
1.5 |
0,41 |
0,2 |
0,04 |
1,0 |
|||
|
1.0 |
0.4 |
0,89 |
1,29 |
0,06 |
144 |
0,98 |
0,71 |
1.33 |
0,21 |
50 |
0,4 |
0,04 |
1,0 |
|
|
0,6 |
0,8 |
0.94 |
—0,02 |
—49 |
0,88 |
0,70 |
1.21 |
0,12 |
0,6 |
0,04 |
1.0 |
|||
|
1.0 |
0,71 |
0,6 |
—0,15 |
—42 |
0.75 |
0,64 |
1.0 |
0,05 |
1,0 |
0,04 |
1,0 |
1*7 <JJ) = —h-------------------------- T^1+..2W+1------------- ,e (4.35)
. ЧР + 1 (V> + }) (V/7* + 2Y4T4/; + О
где Ті, Vi — постоянная времени и коэффициент демпфирования типового звена.
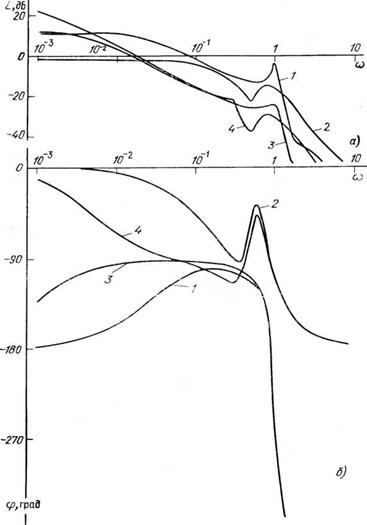
Анализ передаточных функций (4.34), (4.35), проведенный для различных типов асинхронных машин, показывает, что при параметрическом управлении динамические и статические показатели асинхронного двигателя как объекта автоматического регулирования подвержены резким изменениям в зависимости от координат центра разложения, так как параметры, определяющие свойства двигателя (&д, т/, v*)» изменяются при этом в широком диапазоне. Для иллюстрации этих общих выводов в табл. 4.2 приведены значения £д, в табл. 4.4 — значения ц, у і для двигателей MTKF111-6 (РПН, РВН), MTF111-6 (РДС), а на рис. 4.3—4.5 показаны логарифмические амплитудно-частотные характеристики (ЛАЧХ) и фазовые частотные характеристики (ФЧХ) при различных координатах центра разложения.
Рассмотрение передаточной, функции lF2y(p), описываемой
(4.34) или (4.35), позволяет сделать и другой важный вывод: в ней 126
|
РВН |
||||||||||||||
|
Tfs |
■»« |
Ї4 |
*5 |
Is |
"п |
О) |
fl |
її |
■*2 |
■*8 |
■*4 |
|||
|
0,24 |
4,26 |
2,02 |
0,61 |
1,11 |
0,49 |
0,1 |
5,6 |
0,43 |
1,35 |
—72,7 |
4,14 |
0,49 |
||
|
0.25 |
10 |
1,48 |
0,53 |
1,2 |
0,55 |
0,2 |
3,3 |
0,25 |
1,29 |
—22,8 |
4,43 |
0,53 |
||
|
0,31 |
249 |
1,32 |
0,25 |
1,02 |
0,69 |
0.2 |
0,4 |
1,73 |
0,13 |
1.38 |
—35.9 |
3,05 |
0,41 |
|
|
0,39 |
—52 |
0,9 |
0,69 |
1,21 |
0,14 |
0,6 |
1,17 |
0,09 |
1,62 |
—70,2 |
1,97 |
0,36 |
||
|
0,41 |
—49 |
0,77 |
0,63 |
0,99 |
0,06 |
1,0 |
0,7 |
0,05 |
2,04 |
—185,5 |
1,07 |
0,26 |
||
|
0,09 |
35 |
0,21 |
0,99 |
1,06 |
0,1 |
0,1 |
5,6 |
0,43 |
2,23 |
—62,5 |
1,74 |
0,46 |
||
|
0,098 |
. 36 |
0,206 |
0,99 |
1,05 |
0,099 |
0,2 |
3,3 |
0,25 |
1.69 |
-13.1 |
2,56 |
0,58 |
||
|
0,097 |
39 |
0,21 |
0.99 |
1,04 |
0,094 |
0,4 |
0,4 |
1,73 |
0,13 |
1.51 |
—11,68 |
2.56 |
0,5 |
|
|
0,094 |
43 |
0,21 |
0,99 |
1,02 |
0,09 |
0,6 |
1,17 |
0,09 |
1.7 |
—18,8 |
1,86 |
0,4 |
||
|
0,09 |
52 |
0,2 |
0,98 |
0,996 |
0,088 |
1,0 |
0,7 |
0,05 |
2.06 |
—46,8 |
і.06 |
0,27 |
||
|
0,09 |
70 |
0,11 |
0,99 |
1,03 |
0,09 |
0.1 |
5,6 |
0,43 |
2,78 |
—60.6 |
1,05 |
0,33 |
||
|
0,09 |
71 |
o. ll |
0,99 |
1,02 |
0,09 |
0,2 |
3,3 |
0,25 |
2,5 |
—10,9 |
1,53 |
0,5 |
||
|
0,09 |
73 |
0,11 |
0,99 |
1,02 |
0,09 |
0,6 |
0,4 |
1.73 |
0,13 |
1,78 |
—7,1 |
2.02 |
0,55 |
|
|
0,09 |
76 |
0,11 |
0,99 |
1,0 |
0,09 |
0,6 |
1,17 |
0,09 |
1,83 |
—9,42 |
1,69 |
0,44 |
||
|
0,09 |
82 |
0,11 |
0,99 |
0,99 |
0,09 |
1,0 |
0,7 |
0,05 |
2,09 |
—21,1 |
1,04 |
0,28 |
||
|
0,09 |
173 |
0,04 |
0,99 |
1,01 |
0,09 |
0,1 |
5,6 |
0,43 |
3,03 |
—59,6 |
0,61 |
0,2 |
||
|
0,09 |
174 |
0,04 |
0,99 |
1,01 |
0,09 |
0,2 |
3,3 |
0,25 |
3,01 |
—9,66 |
0,89 |
0,33 |
||
|
0,09 |
176 |
0,04 |
0,99 |
1,0 |
0,09 |
1.0 |
0,4 |
1,73 |
0,13 |
2,38 |
—4,49 |
1,31 |
0,51 |
|
|
0,09 |
179 |
0,04 |
0,99 |
1,0 |
0,09 |
0,6 |
1,17 |
0,09 |
2,13 |
—4,62 |
1,34 |
0,48 |
||
|
0,09 |
183 |
0,04 |
0,99 |
1,0 |
0,09 |
1,0 |
0,7 |
0,05 |
2,16 |
—8,11 |
0,99 |
0,31 |
практически всегда присутствует апериодическое звено с постоянной времени тз( табл. 4.4), значительно большей, чем постоянные времени остальных звеньев. Как видно из рассмотрения табл. 4.2 и 4.4, в реальном диапазоне изменения момента и скорости значение постоянной времени тз передаточной функции W2y{p) примерно совпадает со значением механической постоянной времени тм в функции Wly(p), т. е. в передаточную функцию асинхронного двигателя, полученную с учетом электромагнитных переходных процессов, входит составной частью передаточная функция (4.15), соответствующая упрощенному представлению двигателя. Апериодическое звено с коэффициентом усиления kA и постоянной времени тз, зависящей от механической постоянной времени двигателя, определяет частоту сопряжения (соСОпі) низкочастотной (наклон 0 дБ/дек) и среднечастотной (наклон 20 дБ/дек) части ЛАЧХ асинхронного двигателя и ее частоту среза. Частота сопряжения (ысопг) среднечастотной и высокочастотной частей J1A4X зависит от большей из электромагнитных постоянных асинхронной машины. Как правило, из-за указанного соотношения ц в (4,33) Ысопг значительно больше (Осопі - Присутствие в структуре двигателя колебательных звеньев обусловливает резонансный подъем ЛАЧХ, существенно возрастающий при малых уі, а из-за форсиру-
|
Рис. 4.3. ЛАЧХ (а) и ФЧХ (б) двигателя MTKF111-6 при регулировании переменного напряжения: = s=l: 2-Um=1, s=0,2; 3-ит=0,2, s=J; 4-Um=0,2, s=0,2 |
|
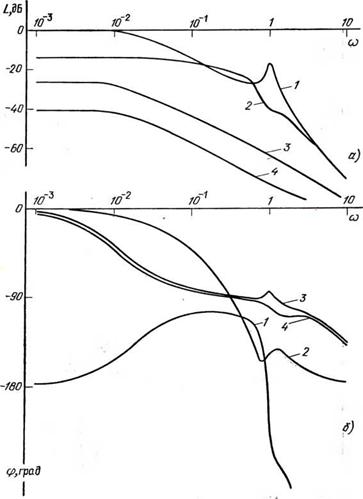
Рис. 4.4. J1A4X (а) и ФЧХ (б) двигателя MTF111-6 при регулировании добавочного сопротивления в роторе: 1 — Г=1, s=l; 2 — Г—1, s=0,2; 3 — г=20, s=l; 4—г=20, s=0,2 |
ющих звеньев второго порядка в JIA4X наблюдается провал. Анализ ЛАЧХ и данных табл. 4.4 также показывает, что из-за появления неминимально-фазовых звеньев не при всех координатах центра разложения асинхронный двигатель оказывается устойчивым объектом регулирования.
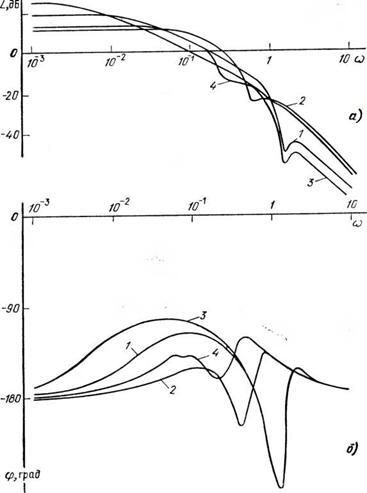
|
Рис. 4.5. ЛАЧХ (а) и ФЧХ (б) двигателя MTKF111-6 при регулировании постоянного напряжения в режиме динамического торможения: £/„=0,4, С0=1; 2 — ип=0,4, со=0,4; 3 — £/„=0,2; со=1; 4 — Un=0,2, (о=0,2 |