ПОЛУПРОВОДНИКОВЫЙ ЭЛЕКТРОПРИВОД
УПРОЩЕННЫЕ МЕТОДЫ РАСЧЕТА УСТАНОВИВШИХСЯ РЕЖИМОВ
Рассмотренные методы, основанные на решении системы дифференциальных уравнений, позволяют получить наиболее точные результаты при расчете установившихся режимов асинхронных
|
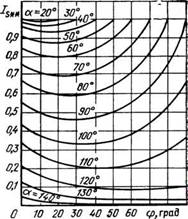
Рис. 2.26. Зависимость /«** Ч(<*> <р) для преобразователя, выполненного по схеме рис. 1.1,а |
|
20 40 60 <р, град |
|
|
|
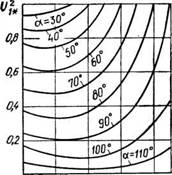
Рис. 2.25. Зависимость U2u=f(a, ф) для преобразователя, выполненного по схеме рис. 1.1,а |
|
Ю 20 30 40 50 60 |
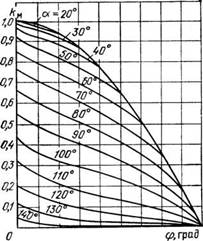
Рис. 2.27. Зависимость ku—f(а, <р) для преобразователя, выполненного по схеме рис. 1.1,а
электроприводов с полупроводниковыми преобразователями, однако требуют применения ЦВМ.
В ряде случаев целесообразно применять более простые модели для получения упрощенных расчетных методик, которые могут быть использованы для определения ряда показателей установившегося режима. Рассмотрим упрощенные методы расчета установившихся режимов при использовании различных схем преобразователей, оценим точность получаемых результатов и определим допустимые границы их применения.
Так, анализ схем ЗТТ при фазовом управлении в статоре показывает, что при изменении угла а происходит регулирование действующего значения первой гармоники фазного напряжения двигателя (Uф) и средний момент р, зависит практически только от £/іф, т. е. составляющими момента от высших гармоник (5, 7, 11, 13 в схеме ЗТТ) можно пренебречь [6]. Значение £ЛФ определяется^ при разложении в ряд Фурье функции uas=f(т). Однако ТОЧНЫЙ ВИД зависимости «as=f(x) может быть получен только при полном описании асинхронной машины и конкретном рассмотре-
нии того или иного асинхронного двигателя. Действительно, при изменении схем включения машины в процессе фазового управления, в частности при реализации несимметричного включения. 2Ф — С, в обесточенной фазе статора наводится ЭДС:
Uas:—Є as-— LDi at Lq (o)Z-oips4~
--iarR2~~toLrifir) /Lr. . (2.113)
Как видно из (2.113), eas, называемая! ЭДС вращения, зависит от скорости двигателя и его конкретных! параметров. Наличие этой ЭДС приводит не только к появлению напряжения Has При ias—0, но и изменяет, как следует из (2.49), напряжения других фаз. И в режиме ОФ — С, когда ias—ibs—ics=0, фазные напряжения статора также не равны нулю, так как в статорных обмотках наводятся ЭДС незатухшими токами ротора.
Следовательно, задача гармонического анализа (отыскания Uiф) при строгом учете ЭДС вращения приводит к необходимости использования рассмотренного метода переменных состояния для исследования установившихся режимов. Наиболее простой приближенный метод анализа установившихся режимов для рассматриваемого случая основан на представлении асинхронного двигателя пассивной эквивалентной активно-индуктивной нагрузкой [6], параметры которой определяются из однофазной схемы замещения. При выборе такой упрощенной расчетной схемы, не учитывающей ЭДС вращения, оказывается возможным провести в общем виде гармонический анализ и получить универсальные расчетные зависимости, позволяющие определить для конкретных электродвигателей U1*, р., /s, kM и др. При использовании Т-образной схемы замещения угол фэ и модуль Z3 эквивалентной нагрузки, зависящие от скольжения, определяются из следующих выражений:
|
(2.114) |
% = h («) = arctg (XJR,),
2, = Ш = VR,‘+X
V 2.
Э ’
где
Ra = Rt-f ---------------------------------- ;---- хэ = Xt+ X0---------- X°HX* ~b^o)—^
(X'2 + X0)* + Я'2/s* (X2' + *0)a + R'l/s2
На рис. 2.25—2.27 приведены универсальные зависимости iA*=f(a, <р), /s**=f(а, ф), ku=f(a, ф), рассчитанные для преобразователя, выполненного по схеме ЗТТ, /в**=/в//б2 — относительное значение действующего тока фазы статора (/б2=^ф^/^э), U2*=U$IU$n. Располагая этими кривыми, можно построить регулировочные механические и электромеханические характеристики и определить энергетические показатели, задавая значения а и рассчитывая по (2.114) для выбранного электродвигателя угол ф, зависящий от скольжения (скорости). Тогда
Я = ) /г, 1 , гч
где ie=MeIMN, Ie*=Ies/IsN — относительные значения момента (Ме) и тока статора (Ies) на естественной характеристике при заданном скольжении.
Значения показателей, рассчитанные по приведенной методике, должны отличаться от полученных при использовании точных методов. Существенного расхождения в расчетах следует ожидать при увеличении скорости и уменьшении среднего момента, когда влияние ЭДС вращения наиболее существенно. Расчеты показывают, что для асинхронных двигателей с увеличенным сопротивлением роторных цепей при (о^О,6^-0,7 и 0,4-МЗ,5 погрешность в расчете среднего момента точными, и, приближенными методами не превышает 15—18%, а для других показателей эта цифра еще ниже. В ряде работ [51—53] рассмотрены возможности учета ЭДС. вращения при расчетах с использованием схем замещения.
Широтно-импульсный преобразователь, применяемый, для регулирования напряжения в статорных цепях (см. рис. 1.2,6), можно представить источником, напряжение на выходе которого не зависит от параметров нагрузки. Схемы же включения асинхронного двигателя являются симметричными при работе ШИП, поэтому для расчета показателей установившегося режима вполне обоснованно может быть использована однофазная схема замещения [10]. Значение Uі* зависит только от параметра у:
Uu=y. (2.116)
Другие же параметры, в частности Is и k^i, связаны с ^ и частотой коммутации fK. Однако, как показано в [10], влияние fK незначительно, поэтому для получения простых расчетных формул целесообразно принять /к=°° (я=°о), тогда
Is**=y, (2.117)
= ]/у cos ср. (2.118)
При известных U* и /s** для конкретных электродвигателей могут быть рассчитаны [і и Is* с использованием (2.115). Сопоставление показывает, что относительные погрешности при расчете значений Is и kM по точным формулам (при п— 1) и по (2.117), (2.118) не превышают соответственно 5 и 1%, если ф^30° и у^ >0,5.
Регулировочные механические характеристики при импульсном управлении в цепи выпрямленного тока ротора аналогичны характеристикам при реостатном управлении [8, 9|, следовательно, при их расчете упрощенными методами необходимо определить эквивалентное сопротивление роторных цепей /?'2Д. Как показано в [9J, при заданном /?д (см. рис. 1.5,а) эквивалентное добавочное сопротивление в цепи выпрямленного тока
Яд.»=Яд(1—Y). (2.119)
При расчете характеристик следует учесть еще влияние трехфазного мостового выпрямителя и, в частности, ввести в цепь выпрямленного тока условнг '
сопротивление Ry, учитывающее снижение выпрямленного напряжения вследствие влияния перекрытия вентилей при работе моста:
3 Хг-{- Х2Г, .0 1Лт
где ke — коэффициент трансформации ЭДС асинхронного двигателя.
Эквивалентное сопротивление в цепи выпрямленного тока Rs=Rn,,r-Ry Приведение R9 к цепи трехфазного переменного тока можно выполнить из условия постоянства мощности, т. е.
R, td*=3RM (2.121)
где Id и І2 — действующие значения выпрямленного тока и переменного тока фазы ротора.
Из (2.121) получаем
J {j-X R, = (2-122)
Трудности определения /?2д связаны с тем, что при работе управляемого мостового выпрямителя отношение Idlh, а следовательно, и коэффициент кг не остаются постоянными. Как указано в [8J, при первом режиме коммутации (когда угол коммутации меньше я/3), k3 изменяется в следующих пределах: 0,5<&з<0,6.
При приближенных расчетах регулировочных характеристик можно пользоваться постоянным значением ks, а также не рассчитывать отдельно Ry, учитывая влияние перекрытия вентилей некоторым увеличением #д, э, по сравнению с определенным из (2.119). Как показывают расчеты, с учетом указанных допущений целесообразно принять й3=0,55-н0,57. Тогда
«^=Фа(1-ї>«д - (2123)
В [54] приведена инженерная методика определения R'2д с учетом значения выпрямленного тока /<г. Зная /?'2д, можно рассчитать характеристики, соответствующие реостатному регулированию. Расхождения в значении среднего момента при использовании точных и приближенных методов расчета не превышают 8— 10%, если y^0,95 и Rb,> (10-г-15)#2-
Анализ режимов тиристорного динамического торможения, реализуемых по схемам одно - и двухполупериодного выпрямления с шунтированием, показывает, что значение среднего момента может быть определено довольно точно, по постоянной составляющей выпрямленного тока /п, а гармонические составляющие не оказывают заметного влияния на значение р. Ошибка в расчете р по (2.31) и по выражению, аналогичному формуле Клосса в режиме динамического торможения, не превышает 2—4 %, если р>0,05.
В схемах выпрямления с шунтированием нет необходимости использовать функцию is=f(т) для определения /п. Напряжение на выходе таких преобразователей не зависит от параметров нагрузки, а однозначно определяется углом ал, поэтому рассчитывается постоянная составляющая выпрямленного напряжения Un, а затем и Ia — UalRs, a, где /?э, п — эквивалентное сопротивление нагрузки по постоянной составляющей. В рассматриваемом случае R3,n=R- Как следует из рис. 2.21,а и 2.22,а:
] * _ 1/Г
Г7П —------ I |,/ 3 sin idi =--------------------------- (1-j-cosa^), (2.124)
fTljK J
ал
где іїі = 1 для схемы двухполупериодного выпрямления, тх= 2 для схемы однополупериодного выпрямления;
/п " 2/^71#! (1+cosa->)- (2.125)
В схеме динамического торможения, реализуемой при использовании ШИП в статоре (см. рис. 1.8,г), значение среднего момента также определяется значением постоянной составляющей тока, которая может быть определена при заданной частоте коммутации. Так, при /к = 300 Гц
|/Г / y31 Y71
7"=І^ГІ|-С08Т+,/з slnVj - (2Л26>
Разница в значении /п, найденном при разложении в ряд функции is^fit) и по (2.125), (2.126), не превышает долей процента.
Таким образом, в ряде случаев гладкая составляющая момента может быть определена с достаточной для практических расчетов точностью при использовании упрощенных методов. При этом системы ФУС и ИУС могут рассматри
ваться как регуляторы первой гармоники переменного напряжения, ШИП в цепи выпрямленного тока ротора — как регуляторы добавочного активного сопротивления, схемы выпрямления для реализации режима динамического торможения — как регуляторы постоянного напряжения. Присутствующие в спектре тока (напряжения) составляющие, кроме полезной, практически не оказывают влияния на момент, развиваемый электродвигателем, а изменяют энергетические показатели электропривода.