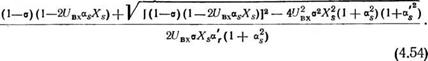ПОЛУПРОВОДНИКОВЫЙ ЭЛЕКТРОПРИВОД
ТЕХНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ СИСТЕМ С АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
Как следует из рассмотрения частотных свойств асинхронного двигателя в «малом», задачу синтеза САУ в общем случае нельзя решить на основе математической линеаризации уравнений асинхронной машины; такой подход возможен, очевидно, только в режиме стабилизации скорости [91], когда электропривод работает при малых отклонениях от координат центра разложения. Строго говоря, используя указанный метод и применяя корректирующие 130
і
|
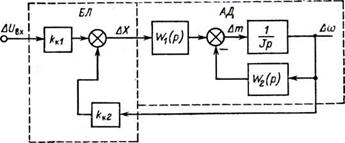
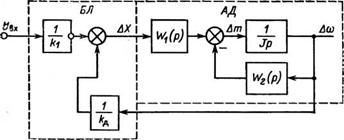
Рис. 4.6. Структурная схема асинхронного двигателя совместно с блоком линеаризации при рассмотрении в «малом» |
устройства неизменной структуры [91], нельзя обеспечить одинаковые показатели качества, а иногда и устойчивость системы даже в режиме стабилизации скорости, если заданные значения скорости различны. При синтезе САУ и построении регуляторов без учета изменяющихся свойств асинхронного двигателя тем более нельзя решить задачу обеспечения стандартных показателей качества, если координаты электропривода (например, при управляемых пускотормозных режимах) изменяются в широком диапазоне.
Задача синтеза САУ с заданными показателями может быть решена путем технической линеаризации нелинейного объекта, т. е. при использовании корректирующих устройств, функционально связанных с изменяющимися параметрами электропривода (м или s, Um, Uu, г) и компенсирующих его нелинейности таким образом, чтобы по отношению к промежуточному входному сигналу (Uвх) объект управления совместно с блоком линеаризации (БЛ) мог быть представлен типовым звеном, параметры которого не зависят от рабочих координат электропривода. Такие устройства могут быть включены в прямой канал и в цепь обратной связи.
Как показано в [93], при создании БЛ может быть поставлена задача выделения в передаточной функции линеаризованного объекта интегрирующего звена с неизменной постоянной времени тн. Для решения указанной задачи (при рассмотрении в приращениях) необходимо охватить объект регулирования корректирующей положительной обратной СВЯЗЬЮ с коэффициентом &К2 И включить в прямой канал усилительное звено с коэффициентом kK (рис. 4.6). Передаточная функция объекта совместно с блоком линеаризации примет следующий вид:
,уг, . ^К1^2у (р)
1 &К2^2у (р)
К іМЛр3 + Л/;2 + Л/Ч-1)
£iP6+£2P4+(£3—'kRkK2A2)p* + (Вь—>kRkK2A3) p+(l—,kakK2)
Приняв Ти =/, что соответствует выделению уже имеющегося в ис-
9* 131
ходной структуре асинхронного двигателя интегрирующего звена 1 Пр, определим из (4.36) значения &К1 и kK2l
ka = №)
Запишем (4.36) с учетом kkl и kki из (4.37), (4.38):
и7і. Лр)= л“
ДІЛ
вх
Ар3 + а*р2 + лзР + 1
в, В2 Во — Л 0 вл — л2 1
|
jp |
[в.-А. Р'+ В,-А, Р + В.-А, Р + В,-А, Р+ J
= _1_|Г(/>). (4.39)
Jp
Значения коэффициентов компенсирующих связей kK, kK2, зависящие от kn, Л3, Bs, будут существенно изменяться при различных координатах центра разложения.
Дальнейшая задача заключается в том, чтобы синтезировать блок линеаризации при рассмотрении системы в «большом», когда параметры электропривода изменяются в значительном диапазоне. Очевидно, техническая линеаризация двигателя, позволяющая исключить влияние нелинейностей объекта на динамические и статические свойства САР, принципиально может быть решена на основе использования выражений (4.37), (4.38), с помощью которых задаются необходимые значения компенсирующих связей при рассмотрении в приращениях. Действительно,
ДХ=ЛкіДС/вх+Лк2Дю, (4.40)
и рассчитываемая при технической линеаризации компенсирующая функция X=fi(UBK, со) должна удовлетворять следующим условиям при заданных координатах центра разложения:
a/,/ (0t/BX) =kKl = (в5-Лз)/ (*д/); (4-41)
df/d(D=kK2— 1 /&д - (4.42)
Однако, как показывает анализ, вычислить первообразную функцию fi(UBX, со) в этом случае не представляется возможным.
Задача значительно облегчается, если для построения блока линеаризации использовать упрощенное описание асинхронного двигателя без учета электромагнитных переходных процессов [94, 96]. Как было показано ранее, при таком рассмотрении момент двигателя является функцией двух переменных, имеющей вид:
РПН
|
(4.43) |
Структурные схемы двигателя при таком описании показаны на рис. 4.7. При представлении асинхронного двигателя звеном с одной (механической) постоянной времени блок линеаризации
выполняется таким образом, чтобы получить следующую пере
даточную функцию линеаризованного объекта:
Л£/вх /Р
Так как Дт=р/Асо, то (4.48) может быть удовлетворено в том случае, если Дт=Л{Увх, или
m=UBX. (4.49)
Условие (4.49) позволяет получить вид функциональной зависимости X=f2 (Uвх, to), реализуемой блоком линеаризации
при его построении на основе упрощенного описания асинхрон
ного двигателя. Подставляя в (4.49) значения момента из (4.2),
(4.3) или (4.4), для разных способов параметрического управления получаем:
|
|
РПН:
(4.50)
|
|
РВН
(4.51)
В (4.50) и (4.51) /2 (со) = l//j (со);
|
(4.52) (4.53) |
РДС
Г =/аИМ^вх).
|
где |
/2 (со) =1 — со;
|
|
Укажем, что при подстановке (4.54) в (4.52) определяется одно из двух возможных значений г, обеспечивающих работу электропривода в заданной точке. При расчете г с использованием
(4.54) двигатель при заданных т и s будет работать на устойчивой части механической характеристики, когда s<sK.
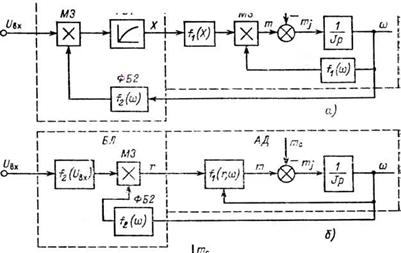
Структурные схемы асинхронного двигателя, линеаризованного на основе упрощенного описания, приведены на рис. 4.8. Как следует из приведенных выражений, функциональный блок ФБ1 (рис. 4.8,а) осуществляет операцию извлечения квадратного корня. С помощью (4.44), (4.46) рассчитывается ФБ2 на рис. 4.8,а, с помощью (4.53), (4.54)—ФБ2 и ФБ1 на рис. 4.8,6. Для иллюстрации на рис. 4.9 приведены функциональные зависимости для конкретных двигателей. Так как максимальный момент т1Пах— =mK, ТО U вхтах== Ш к. Это ЗНЭЧеНИе U вх является предельным в
(4.54) . При Uвх^-> Uвхтах подкоренное выражение в (4.54) принимает отрицательные значения. Отметим, что у ряда двигателей (например, краново'металлургическигх серий), имеющих экскаваторную естественную характеристику, коэффициент k2 (см. рис. 4.1) при регулировании переменного напряжения очень мало зависит от скорости в большом диапазоне ее изменения. В этом случае из БЛ может быть исключен функциональный блок ФБ2, а если не используются другие способы параметрического управления, кроме РПН, то и множительное звено.
Рассмотрим передаточные функции и частотные характеристики асинхронного двигателя с учетом электромагнитных переходных процессов при применении БЛ, реализованного на основе 134
|
|
|
1 |
т ^ |
mJ, |
1 |
|
Jp |
|
Рис. 4.8. Структурные схемы технически линеаризованного асинхронного двигателя при упрощенном описании (ФБ1, ФБ2 — функциональные блоки): о — РПН, РВН; б — РДС; в — эквивалентная схема по промежуточному входному сигналу |
|
|
|
(UBX) для всех способов параметрического управления |
|
fi(o) |
|
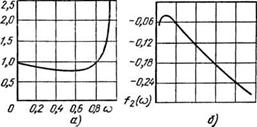
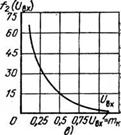
Рис. 4.9. Зависимость /г(о>) для двигателя MTKF111-6 при регулировании переменного (а) и постоянного (б) напряжения и зависимость f2—f(UBX) для двигателя MTF111-6 при регулировании добавочного сопротивления |
|
|
|
О 0,2 0£ 0,6 О, в со |
упрощенного описания асинхронной машины. При исследовании в «малом» получаем
АХ = />Ы^. И) ш jhggi м> дш. (4.55)
оивх ди>
Определение частных производных функции /г(£Лзх, to) по
(4.50) , (4.51), (4.54) показывает, что для различных способов
|
Рис. 4.10. Структурная схема линеаризованного асинхронного двигателя в «малом» при синтезе блока линеаризации по упрощенному описанию |
параметрического управления справедливы общие соотношения
df2(U„, v)/dUBX= 1/Л,; (4.56)
df2(U„, со)/дсо=1/&д. (4.57)
Структурная схема двигателя совместно с блоком линеаризации
для этого случая приведена на рис. 4.10. Передаточная функция, соответствующая структуре рис. 4.10, принимает следующий вид:
тт^ / . Асо W2y(р) __
ал [Р) ~ А^вх ~
__ ________________________________ Р3 ~Ь АгР2 Ч~ - А3р -|- 1______________________________
I В, В2 В3 — Ах а В4 — А2 1
|
k2(Bi |
- Л)^+^+^+- л"+’ J
±-W'(p), (4.58)
1-р
где
= k,(B5-A3). (4.59)
Анализ требуемых (4.41), (4.42) и полученных при упрощениях (4.56), (4.57) корректирующих связей, а также рассмотрение соответствующих передаточных функций (4.39), (4.58) показывает, что df2/d(i)=dfi/d(i). Это позволяет в обоих случаях выделить в передаточной функции интегрирующее звено. Однако если в (4.39) всегда ти=/, то при создании БЛ по упрощенному описанию конкретное значение постоянной времени т'и (4.59) зависит от способа параметрического управления.
Так, при РПН
V = / + К ЄС +-ft_+ aar'r ь a' + ¥..' (4.60)
и ' 1 2 ae + bf 2 o2 + 62
Анализ показывает, что для асинхронных двигателей с повышенными коэффициентами затухания рассчитанная по (4.60) т'и»/, т. е. т'и~ти. Для иллюстрации этого вывода в табл. 4.5
|
РПН |
PBH |
|||||
|
Um |
s |
9 CD cp |
Un |
CO |
І CO cp |
|
|
1,0 |
1,0 |
0,0399 |
0,4 |
1,0 |
—0,86 |
0,0419 |
|
1,0 |
0,1 |
0,0360 |
0,3 |
0,6 |
-0,79 |
0,042 |
|
0,2 |
1,0 |
0,0401 |
0,2 |
0,6 |
—0,35 |
0,0409 |
|
0,2 |
0,1 |
0,0399 |
0,1 |
0,2 |
—0,23 |
0,0345 |
|
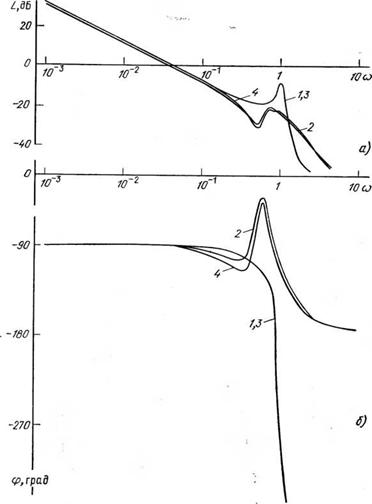
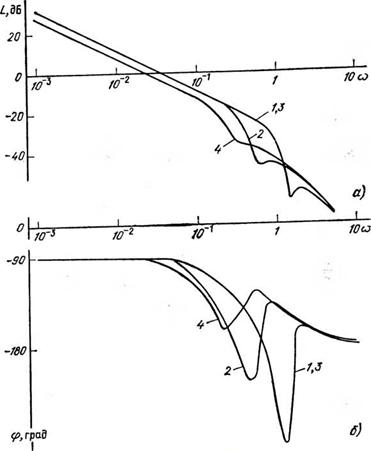
Рис. 4.11. ЛАЧХ (а) и ФЧХ (б) линеаризованного асинхронного двигателя MTF111-6 при регулировании переменного напряжения: 1 — Um=l, s=l; 2~um=l, s=0,2; 3 — Um=0,2, s=l; 4 — Um=0,2, s=0,2 |
приведены частоты среза со'СР= 1 /т'и для двигателя MTKF111-6, у которого ти=/ = 24,93, a g>cP= 1/ти=0,0401.
При РВН
«г ' — J I /з [ 2(] — °)а/гагг2й)а, grr(a/+grV) — Ц2 _ у ~] ^ gj.
L <К“г04-“41 'КО2 - to2] (су^ + со2 ]' 1 * }
В этом случае значения т'и могут существенно отличаться от ти=/. Эти различия увеличиваются с возрастанием момента (значения Un) и уменьшением скорости двигателя. Анализ показывает, что у асинхронных двигателей с повышенными коэффициентами затухания разница между ти и т'и не превышает 30—35%, если ц^1 (t/n^0,3-^-0,4), ю^0,2. Обычно при соС С0,2 т'и>ти, следовательно, и реальное быстродействие будет
|
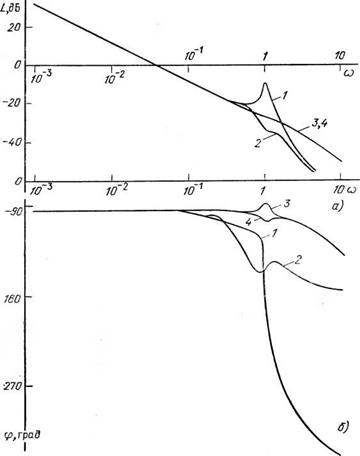
Рис. 4.12. ЛАЧХ (а) и ФЧХ (б) линеаризованного двигателя MTKF111-6 при ререгулировании добавочного сопротивления: / —г= 1, s=l; 2 — г= 1, s=0,2; 3 — г=20, 5=1; 4 — Г=20, s=0,2 |
|
Рис. 4.13. ЛАЧХ (а) и ФЧХ (б) линеаризованного двигателя MTKF111-6 при регулировании постоянного напряжения в режиме динамического торможения: / — £/„=0,4, ю=1; 2 — £/„=0,4, <о=0,4; 3 — £/„=0,2; (0=1; 4 — £/„=0,2, со=0,2 |
меньше, чем рассчитанное из условия ти=/, т. е. изменение со'ср не может привести к неустойчивой, работе САУ, синтезированной в предположении, что TH=/=const. В табл. 4.5 приведены некоторые значения (о'ср для двигателя MTKF111-6 при регулировании выпрямленного напряжения.
При РДС значения коэффициентов В5 и Л3 таковы (см. табл. 4.3), что T'H=/=const при любых координатах центра разложения, т. е. в этом случае даже при построении БЛ на основе упрощенного описания асинхронного двигателя всегда обеспечивается T/n=Tn=/ = COnst.
Таким образом, как показывает анализ, при технической линеаризации асинхронного двигателя, реализуемой по упрощенно
му описанию, в передаточной функции линеаризованного объекта (4.58) удается выделить интегрирующее звено, постоянная времени которого т'и остается неизменной или изменяется несущественно при реальном диапазоне изменения координат электропривода. Значение т'и значительно больше, чем постоянные времени остальных типовых звеньев, входящих в (4.58). В связи с этим частота среза J1A4X передаточной функции (4.58) определяется значением т'и (соСр—1/т'и), т. е. при указанном способе линеаризации обеспечивается наклон 20 дБ/дек в среднечастотной части J1A4X и практически одинаковое быстродействие электропривода при различных координатах его рабочих точек, так как частота среза J1A4X изменяется незначительно. При правильном выборе полосы пропускания внутреннего контура регулирования САУ и ограничении ее таким образом, чтобы электромагнитные переходные процессы, определяемые параметрами звеньев (Передаточной функции W'{p), не могли оказать влияния на динамику электропривода, линеаризованный асинхронный двигатель при различных способах параметрического управления может быть представлен интегрирующим звеном с постоянной времени їй=/ в соответствии со структурной схемой рис. 4.8,в.
Анализ передаточных функций (4.33) и (4.58) показывает [96], что при рассмотренном способе линеаризации происходит изменение только свойств апериодического звена &д/(тзр+1)
(4.34) , (4.35) и его преобразование в интегрирующее звено с постоянной'времени tV Параметры же остальных звеньев (4.33), определяющих вид электромагнитных переходных процессов, остаются практически без изменения.
Частотные характеристики линеаризованного двигателя при различных способах/ параметрического управления приведены на рис. 4.11—4.13.