ПОЛУЧЕНИЕ КОМПОЗИЦИОННЫХ. ГРАНУЛИРОВАННЫХ МАТЕРИАЛОВ. В ПЛАНЕТАРНОМ ГРАНУЛЯТОРЕ

. Кинетика гранулообразования в аппаратах барабанного типа

В процессе гранулирования выделяют 3 этапа. На начальной стадии процесса образуются ядра, размер которых не превышает 0,1-0,5 мм. На втором этапе роста ядер избыточная влага выдавлива­ется на поверхность гранул. Влажная оболочка ядра обеспечивает
рост гранул за счет простого наслаивания или агломерации ряда час­тиц. На заключительной стадии процесса происходит рост гранул и их дробление на более мелкие частицы. Рост гранул оценивается уменьшением удельной поверхности гранулы в виде следующего уравнения:

ln (F - Fo) = ка + С, (1.16)

где F - удельная поверхность ядер на единицу объема; га - частота вращения барабана; к - константа скорости роста;

F0, С - постоянные, определяемые из экспериментальных дан­ных.

Известны и другие работы, в которых рассматриваются различ­ные механизмы образования гранул в зависимости от размера исход­ных частиц. Принимая, что движущей силой процесса гранулирова­ния является сила сцепления частиц в агломерате, авторы рабо­ты [15] предлагают следующую зависимость для расчета среднего размера гранул:

dсp = do exp m(Qx - Qo)n, (1.17)

где d^ - средний диаметр гранул;

d0 - диаметр гранул в начальный момент гранулирования;

Q* - содержание жидкой фазы;

Q0 - содержание жидкой фазы в момент начала гранулирования;

m, n - эмпирические коэффициенты, определяемые опытным путем.

Для веществ, не растворимых в связующем, в работе [16] при­нимают, что движущая сила целиком определяется количеством свя­зующей жидкости, вводимой извне, т. е. влагодержанием шихты. При этом Qж = и.

Средний диаметр гранул зависит также от количества вводимого су­хого ретура g и размера частиц ретура dp. Чем больше ретура и чем он крупнее, тем меньше поверхность частиц и выше их влагосодержание.

Диаметр гранул может определяться по формуле

(1.18)

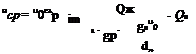где gp - относительное количество ретура в продукте.

Эта формула справедлива лишь в случае, если ретур не погло­щает влагу.

Реально используемый для удобрений, ретур при смешении с влажным порошком с течением времени насыщается влагой. Со­держание жидкой фазы на поверхности окатываемых частиц при этом уменьшается на то количество влаги, которое диффундировало внутрь гранул ретура, т. е. на величину ug (где ир - влагосодержание ретура). Влагосодержание ретура зависит от времени контакта, тем­пературы и т. д. Поэтому авторы [16] приводят расчетную формулу для определения среднего диаметра гранул, полученных методом окатывания, к следующему виду:

n

Эта зависимость может быть использована только при условии [1]

Влагосодержание шихты превышает минимальное значение, не­обходимое для гранулирования. При Qобщ < Qж гранулообразование не происходит.

Исследования процесса роста гранул влажного песка показали, что максимальный размер частиц тем меньше, чем меньше поверх­ностное натяжение связывающей жидкости.

Рассмотренные выше зависимости для расчета роста гранул и установленные закономерности гранулирования, как правило, но­сят частный характер. Их применение ограничено условиями тех экспериментов, данные которых необходимо использовать в расчет­ных выражениях.

В работах [11, 17] принято, что все мелкие частицы накатыва­ются на крупные, равномерно распределяясь по их поверхности сло­ем одинаковой толщины, независимо от размера зародышей. Полу­чено следующее уравнение для расчета размера гранул:

(1.21)

V рнас )

где di - диаметр исходного зерна, м; р - плотность крупных частиц; рнас - плотность комкуемого материала в неокатанном состоянии [11],

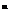a - -

где pm - количество комкуемого материала;

p - то же, в каждой фракции.

Отношение поверхности комкующих фракций к объему мелких комкуемых фракций названо коэффициентом скорости гранулирова­ния кс. г. Чем больше коэффициент кс. г, тем быстрее мелочь накатыва­ется на крупные зерна. В этом коэффициенте не учтены параметры, характеризующие природу материала, способность его взаимодейст­вовать с водой, поэтому кс. г интересен лишь для идеального случая принятого механизма гранулообразования. Исходя из того же меха­низма гранулообразования, для расчета среднего размера гранул по­лучено уравнение [18]:

d 0exp3m(W - W0) - d d - d + t,

t

где тср - среднее время пребывания материала в грануляторе, с; т - текущее время, с;

dq, - средний диаметр исходных частиц, м;

d0 - диаметр частиц, соответствующий началу гранулообразования;

W0 - минимальное содержание связующего, при котором начи­нается гранулообразование;

m - экспериментально определяемый коэффициент, характери­зующий свойства гранулируемого материала.

Уравнение (1.22) справедливо лишь для гранулирования мето­дом наслаивания и поэтому применимо в узком интервале изменения режимных параметров [11].

Механизм равномерного наслоения подтвержден для некоторых случаев экспериментально. В работе [3] отмечено, что приращение массы гранул прямо пропорционально d2, здесь же указывается на прямо пропорциональную зависимость количества налипающей ме­лочи от площади свободной поверхности. Это явление обнаружено при имитации непрерывного процесса периодическим удалением части мелких гранул из аппарата.

Таким образом, в рассмотренных работах утверждается, что скорость роста гранул в непрерывном процессе не зависит от их раз­мера, а в периодическом процессе, когда мелочь для наслоения не загружается извне, не образуется в результате истирания небольших агломератов, скорость увеличения диаметра гранулы тем выше, чем больше гранула.

Схема процесса, в котором каждый зародыш покрывается толь­ко одним слоем исходного вещества, рассмотрена в работе [11]. Предложена формула для расчета диаметра гранул:

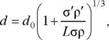(1.23)

где d0 - диаметр зародыша, м;

а' - объемная доля твердого вещества в зародыше; р' - плотность материала зародыша, кг/м3;

L - соотношение масс зародыша и слоя; а - объемная доля твердого вещества в слое; р - плотность частицы, кг/м3.

Отмечается, что частицы радиусом более 0,6 мм всегда будут действовать, как зародыши. Основным фактором, определяющим выход гранул, как отмечает автор, является эффективность, с кото­
рой слой прилипает к ядру. Этого-то показателя как раз и нет в урав­нении (1.23). Оно, как и уравнения (1.21), (1.22), пригодно только для частных случаев послойного роста гранул.

Приведенные выше формулы позволяют определить средний размер частиц после гранулирования. Как известно, продукт всегда имеет некоторое распределение по размерам, и этот показатель явля­ется важным.

Авторы [11] рассматривают процесс гранулирования в барабане как объединение мелких зародышей, беспорядочно движущихся и перемешивающихся в плотном слое. Частота столкновений являет­ся функцией размера данного зародыша и распределения размеров остальных зародышей, а также динамических характеристик бараба­на. С учетом функции вероятности основное уравнение кинетики гранулирования для фракций i и j имеет вид

где Х(т) = kp(x)/2 - функция скорости агломерации;

Р(т) - функция интенсивности столкновений, порозности заро­дышей, их размера, способности к деформации, пластичности;

ni(x), njx) - число зародышей определенного размера, имеющих объем Vi и Vj;

N(t) - полное число зародышей в системе на время т.

При суммировании уравнения (1.24) по всем размерам гранул получается:

^N^ =-X(t)N (т). (1.25)

dx

После ряда преобразований автором получены уравнения для определения доли фракций гранул объемом более Vi:

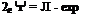(1.26)

Уравнения (1.25), (1.26) справедливы для периодического про­цесса. Распределение гранул по размерам стремится к линейной за­
висимости. Отношение максимального размера гранул к минималь­ному в этой линейной области распределения является величиной постоянной и не превышает 3.

Используя механизм дробления и наслоения, авторы [11] пока­зали, что его действие приводит в конечном итоге к некоторому ус­тойчивому распределению гранул по размерам, описываемому урав­нением

(1.27)

где dm - медиана распределения;

R(d/dm) - кумулятивная фракция частиц, размер которых равен или превышает данный размер гранулы;

dx - размер максимальной гранулы;

в - функция dm/dx, которая остается неизменной в ходе процесса.

Распределение (1.27) резко заканчивается при R = 1, в то время как эксперименты указывают на наличие определенного «хвоста» в области мелкодисперсных гранул. Поэтому при R > 0,7-0,9 опыт­ные данные не согласуются с уравнением (1.27). Указывается, что причиной этого несоответствия может быть принятое допущение о том, что при столкновении разрушаются только наименьшие грану­лы [3]. Более рационально предположить, что существует опреде­ленная вероятность разрушения гранул всех размеров, но вероят­ность разрушения самых мелких гранул наиболее велика.

Кинетика периодического процесса гранулирования, достигае­мого дроблением и наслоением, описывается в [11] уравнением со­хранения количества гранул:

B(x, т) - фракция гранул размером (объемом) х, разрушающихся в единицу времени;

G(x, F) - скорость роста гранул размером выше х из дробленого материала, объем которого F(t).

Скорость роста и функция разрушения В зависят от природы вещества и, следовательно, могут быть уточнены только опытом.

Приведенные уравнения (1.26), (1.27), (1.29) позволяют рассчитать гранулометрический состав продукта в периодическом процессе, т. е. при одновременных вводе сырья и выгрузке продукта, методика расчета должна учитывать распределение по времени пребывания.

В работе [11] предложен аналитический метод расчета диаметра частиц при гранулировании с использованием грануляторов бара­банного типа. В процессе гранулирования во вращающемся слое ка­ждая частица совершает движение двух видов: вращательное и по­ступательное. Предполагается, что температура слоя гранул не изме­няется по длине гранулятора, то есть рассматривается изотермиче­ский установившийся процесс гранулообразования. На частицу раз­мером d за один оборот её вокруг собственной оси наслаиваются другие частицы, образующие пленку толщиной X. Авторы предпо­ложили, что при движении гранулы по спиралевидной траектории на протяжении пути А/ ее диаметр увеличивается на величину Ad, рав­ную 2NX:

(1.30)

где N - число оборотов гранулы вокруг своей оси на пути А/; X - толщина наслаивающейся пленки.

С другой стороны, А/ определяется как

(1.31)

где Яб - радиус барабана;

а - угловая частота вращения барабана; а ос - скорость движения продукта вдоль оси барабана;

AL6 - длина барабана.

Обозначая в уравнении (1.31) А£б/а через Ат, с учетом (1.30) по­сле дифференцирования получается:

ddd = ^ -^^Ыт. (1.32)

Это уравнение представляет собой математическую модель рос­та частиц при гранулировании методом окатывания.

В общем случае изменение гранулометрического состава во времени может быть описано уравнением

p(d)d[p(d)] = f 2^6Ю Jp(X)dT, (1.33)

где p(d) - массовая плотность распределения частиц по размерам; р(Х) - плотность распределения пленок, наслаивающихся на

пути А/.

На практике гранулометрическая характеристика материала оп­ределяется ситовым анализом и представляется дискретными фрак­циями. Тогда уравнение (1.33) для /-го интервала можно записать следующим образом [3]:

2R аХ jdx

п

До сих пор рассматривались идеальные процессы роста гранул при условии неизменности структуры, отсутствия истирания, дроб­ления и других сопутствующих процессов, приводящих к изменению размера гранул [3].

Реальные процессы гранулирования, протекающие в плотных гравитационных слоях дисперной фазы, сопровождаются, как прави­ло, уплотнением структуры формируемых гранул, их истиранием, измельчением и т. п.

Учитывая тот факт, что при гранулировании порошкообразных материалов окатыванием наряду с процессами роста гранул проте­кают процессы, проводящие к уменьшению их размеров, под толщи­ной наслаиваемой пленки необходимо понимать разность:

Х = Хir - Хiu, (135)

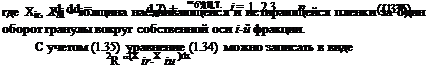Рассмотрим частные случаи модели (1.36) [11]. Пусть Xir = const и Xiu = 0, т. е. предполагается, что в течение всего времени гранулиро­вания на гранулу i-го размера наслаивается на каждом отрезке А/ пленка одинаковой толщины Xir. Примером может служить процесс гранулирования при значительном избытке ретура, т. е. когда по всей длине гранулятора вероятность столкновения гранулы с наслаиваю­щимися частицами одинакова. В результате интегрирования уравне­ния (1.36) получается

Пусть при т = 0 величина Xir = d^, т. е. в начальный период про­цесса гранулирования происходит агломерирование частиц началь­ного размера di0. При увеличении т величина Xir ^-0, т. е. на гранулу наносится пленка все меньшей толщины вследствие уменьшения ве­роятности столкновения гранулы с наслаивающимися частицами (их число со временем уменьшается). Такой механизм наблюдается при гранулировании увлажненной шихты с подачей незначительного ко­личества сухого ретура. В этом случае можно рассмотреть два вари­анта решения модели (1.36). Если толщина наслаиваемой на гранулу пленки уменьшается по длине барабана по линейному закону

Xi = dt0 - £jT, (1.38)

где k1 - кинетический коэффициент, зависящий от свойств гранули­руемого материала и параметров процесса, то при Xu = 0 получается:

dt = 2R“ dx. (1.39)

n(d,0 - ^т)

После интегрирования выражения (1.39) получим:

dt d ^j(di0 - Мт. (1.40)

Если толщина наслаиваемой пленки уменьшается по экспонен­циальному закону

X i = dt 0exp( - k2 т), (1.41)

где k2 - кинетический коэффициент, то выражения (1.36), (1.41) при Xiu = 0 преобразуются:

dtddt = 2R^ . (1.42)

ndi0 exp(-k2T)

После интегрирования выражения (1.42) получим:

di = dio + 4d'0RGЮ [1 - eXP( k2т)]. (1.43)

nk 2

В общем случае, когда Xir « Xiu, решения уравнения (1.36) прини­мают боле сложный вид. Подставляя в эти уравнения экспериментально полученные кинетические коэффициенты X и решая совместно с урав­нением распределения по времени пребывания в данном грануляторе, можно рассчитать гранулометрический состав продукта для любых ус­ловий гранулирования в аппаратах барабанного типа [11].