Расчет составов полимербетонов
Определение оптимальной толщины пленки связующего, обусловливающей максимальную прочность, проводилось нами на смоле ФАМ вязкостью 20 с по ВЗ-4, которая была принята эталонной. При постоянном расходе связующего изменялось количество наполнителя, имеющего одинаковую удельную поверхность. Из приготовленной мастики формовали литые цилиндрические бездефектные образцы и стандартные лопатки (ГОСТ
11262—68) п определяли предел прочности при разрыве.
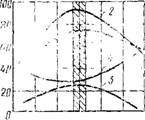
Результаты испытании показали, что с увеличением количества наполнителя прочность на разрыв повышается, достигает своего максимума, а затем падает. Оптимальная толщина пленки связующего вокруг зерен наполнителя соответствует' максимальной прочности мастики (рис. 12). Аналогичная закономерность при определении прочности эпоксидных мастик в зависимости от удельной поверхности кварцевого наполнителя отмечена в [141]. Обобщенная зависимость прочности полимерной мастики о г дисперсности наполнителя характеризовалась максимальным значением в интервале 2000— 3000 см2/г.
С увеличением до определенного предела степени наполнения экстремально изменяются средняя плотность, пористость и прочность при сжатии и изгибе. При этом экспериментальные значения этих характеристик распределяются в довольно узкой области (см. рис, 12).
Следовательно, оптимальному содержанию в системе наполнителя соответствует определенная структура и комплекс оптимальных физико-механических сзойств, названный нами правилом экспериментальных значений [1І7]. Из этого правила следует, что если у правильно подобранного состава материала две-три определенные характеристики оптимальны, то можно с достаточной уверенностью предполагать, что и ряд других характеристик будет иметь оптимальные значения.
|
/>,иф R^jMfla JflfflJ |
|
У. уПП 1500 Woo 500 |
|
50 100 150 200 250 300 КоличестЪо наполнителя,% |
|
Рис. 12. Изменение характеристик полимерных мастик в зависимости от содержания наполнителей 1 — плотность; 2 — предел прочности при сжатии; 3 — предел прочности на растяжение при изгибе; 4 — пористость |
Таким образом, можно сделать очень важные выводы. для каждого вида термореактивною синтетической смолы и минерального наполнителя существует строго определенная степень наполнения, обеспечивающая максимальную прочность мастики; уменьшение или увеличение степени наполнения приводит к значительному
падению прочности системы; оптимальное количество
Наполнителя определяется не только природой синтетической смолы и наполнителя, но и дисперсностью последнего.
Зная закономерность изменения прочности в зависимости от степени наполнения, вязкость синтетической смолы и удельную поверхность наполнителя, можно вычислить математическую зависимость этих величин и дать расчетную формулу для определения минимально необходимого количества связующего при составлении рецептуры той или иной мастики.
Исходя из экспериментальных данных толщина пленки может быть рассчитана по формуле
Где б —толщина пленки связующего, см; Vcb — объем связующего, см[6]; 5н — удельная поверхность наполнителя, см3/г; тк — масса наполнителя, г; г)уСл — отношение фактической вязкости смолы ФАМ к вязкости этой же смолы, принятой за эталон (20 с по ВЗ-4).
После преобразования формула принимает более удобный для расчета вид:
Б = тсъ %сл/(5Уд тн рсв), (12)
Где /Лев — масса связующего, г; ірсв — плотность связующего, г/см3.
Расчеты показывают, что для оптимальных составов полиэфирных, фурановых и других мастик приведенная толщина пленки связующего вокруг каждого зерна наполнителя составляет 1,5—2 мкм, а общая толщина пленки между зернами в монолитной композиции колеблется в пределах 3—4 мкм.
Тогда расход связующего для мастики определяют по формуле
Бмаст = (Sh тн рсв6>|усл) Ю-3J,] (13)
Где Омаст —оптимальный расход связующего для мастики, кг; SH — удельная поверхность наполнителя (минеральной муки), см2/кг; тн — масса наполнителя, кг; рсв — плотность связующего, кг/дм3; ё—толщина пленки связующего (б«0,00015 см).
Расчеты количества связующего по формуле (13) показывают, что в этом случае отношение связующее: наполнитель составляет 1:1,5—1:2. Мастики с таким количеством наполнителей обладают максимальной прочностью и жесткостью.
Для известного гранулометрического состава сухой смеси заполнителей оптимальное количество связующего для полимербетона находят по формуле
G„.6=[K{Simi + S2m3 +S3m3 + S„ )рсвб%сл]10-3, (14)
Где Gп. б — оптимальное количество связующего для полимербетона принятого состава, кг; Si; S2; S3 и S„~ удельная поверхность заполнителей различных фракций (щебень крупный, щебень мелкий, песок), ^см2/кг; пи, т2, т3 и mn — масса заполнителей различных фракций, кг; К.—коэффициент, учитывающий увеличение количества связующего, необходимого для раздвижки зерен заполнителя мастикой, /(=1,05.
Для определения удельной поверхности мелкодисперсных наполнителей разработано большое количество различных приборов, методика определения достаточно подробно изложена Г. С. Ходаковым [143].
Удельную поверхность заполнителей с достаточной для практических целей точностью можно вычислить методом ситового анализа по формулам:
Яуд. п = 0,06 [аі {qi /рПі) Ki + а2 (q2 /рПг) Кї + а3 (qz /рп„) X
ХКз+Щ (Яі /рп,) Ка + as (<7s /рП5) Кб]', (15)
5уД. щ = 0,06 [aL (qi /рЩі)К"і + а2 {q2 /рЩг) Кч + аз (q$ /рЩ]) X X Кз + а4 (qi /рщ<) Кі + аь (дь /рЩб) Кь ], (16)
Где 5уд. п и 5уД. щ — удельная поверхность песка и щебня соответственно, см2/кг; а — пустотность заполнителей; qi, q2, q3, qt, q5 — остаток заполнителя, г (при навеске 1 кг), на ситах с отверстиями соответственно 2,5; 1,2; 0,6; 0,3 и 0,15 мм для песка и на ситах с отверстиями соответственно 5, 10, 20, 30 и 40 мм для щебня; ipn и Рщ—плотность песка и щебня, кг/дм3; Ki, К2, Кз, Кі, Ка— соответственно коэффициенты геометрической формы заполнителей.
Значения коэффициентов К и а могут быть приняты но таблицам, приведенным в [23].
Таким образом, зная удельную поверхность наполнителей и заполнителей, количество синтетического связующего для полимербетонов оптимального состава определяют по формуле (14). Однако она не позволяет установить в каждом конкретном случае размер зерен заполнителя и оптимальное соотношение между отдельными фракциями.
Существуют два принципиально различных способа подбора гранулометрического состава плотных смесей многокомпонентных систем: с прерывистой и непрерывной гранулометрией. Первый способ не нашел достаточного распространения при подборе составов цементных бетонов ввиду некоторой сложности определения прерывистости фракций и дополнительных расходов, связанных с рассевом щебня и песка. Кроме того, как показали исследования Б. Г. Скрамтаева, К. Г. Зеленова, В. В. Кураєва и других авторов, при использовании смесей с прерывистой гранулометрией не было получено преимуществ, оправдывающих эти дополнительные расходы. Так как даже незначительное снижение расхода полимерного связующего, которое может дать сверхплотный подбор составов заполнителей, приводит к значительному снижению стоимости полимербетонов, то в этом случае экономически целесообразно пойти на подбор составов с использованием прерывистой гранулометрии.
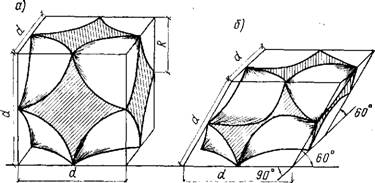
Если рассмотреть наиболее плотную упаковку зерен заполнителей на геометрических моделях, состоящих из однородных шаров, то оказывается, что минимальным количество шаров в единице объема будет в том случае, когда центры их совпадают с узлами кубической решетки (рис. 13,а), и максимальным — при ромбоэдрической укладке (рис. 13,6). Тогда коэффициент заполнителя объема при укладке шаров одинакового диаметра может быть определен по формуле
/Csan = ^'[6(l —cosGKi + 2 cos 01. (17)
Отсюда для кубической укладки шаров (0 = 90°) Кзап = 0,5236, а ДЛЯ ромбоэдрической (0 = 60°) Кзал = = 0,7405. Следовательно, при изменении угла от 60 до 90° пустотность колеблется в пределах 0,4764—0,2595.
Если эти пустоты последовательно заполнять шарами соответствующего диаметра, то теоретически можно получить коэффициент заполнения, бесконечно близкий к единице.
Акад. Н. В. Белов считает, что при кубической укладке шаров одинакового диаметра образуются октаэдриче - ские пусготы, а при ромбоэдрической — тетраэдрические по типу геометрических фигур, образуемых шарами вокруг соответствующей «дырки» (рис. 14). Для случая бесконечной укладки шаров можно рассчитать количество пустот каждого сорта, приходящихся в среднем на один шар.
Если при плотной упаковке пустоты заполнить соответствующими им по диаметру шарами, то нетрудно подсчитать, что шар, наиболее плотно заполняющий октаэдр ическую пустоту, имеет диаметр, равный 0,414 диаметра основного шара, а диаметр шара для тетраэдр и - ческой пустоты составит 0,225 диаметра основного шара (рис. 15).
Для шаров одинакового диаметра наиболее вероят-
3* Зак, 251
|
Плотной укладки шаров |
Рис. 13. Кубическая (а) и ромбоэдрическая (б) схемы
|
Рис. 14. Размеры и геометрическая форма пустот, образованных в результате кубической (а) и ромбоэдрической (б) укладки шаров |
Рис. 15. Схема заполнения пустот шарами эквивалентного диаметра
|
-0,225£>„ |
|
Змакс |
Ная и устойчивая форма укладки — ромбоэдрическая. Иная картина наблюдается при укладке шаров различного диаметра. Например, коэффициент заполнения произвольного объема гранулами полистирола случайного гранулометрического состава колеблется в пределах 0,58—0,62. Это говорит о том, что укладка гранул полистирола, которые являются почти идеальными шарами, более близка к кубической. Кроме того, как указывает акад. Н. В. Белов, значительная часть существующих в природе минералов тоже имеет кубическую упаковку. Следовательно, с достаточным основанием можно предположить, что укладка зерен заполнителя также должна иметь кубическую упаковку. Тогда, если обозначить диаметры основных шаров через Dь а диаметр шаров, заполняющих соответствующие пустоты, через D2, Dз и т. д, то для строго кубической упаковки и бесконечной укладки шаров имеется следующая математическая зависимость: Dj :D2 : D3=l : ] : 2. При этом D2=0,414Di и
D3 = 0,224Ј>;.
При отклонениях размеров щебня от среднего размера максимальные диаметры последующих шаров не могут быть больше размеров пустот, образованных минимальными размерами основного шара. В этом случае
£)2макс = 0,414/)1Мин и Д
Если принять £>1 = 1, то объем, занимаемый тремя фракциями щебня, составит: D + D2+D3 = 0,5230+0,037+ + 2(0,0057) =0,5714.
Видно, что третья фракция щебня увеличивает степень заполнения примерно на 1%. Поэтому для полимербетона с максимальной крупностью щебня до 30 мм можно рекомендовать одну фракцию щебня, а для полимербетонов с крупностью щебня 35—50 мм — две фракции. В этом случае одна фракция щебня D{ займет 52,3% объема, а две фракции D{--D2= 56% объема. Объем пустот составит: V, = 1—0,52 = 0,48 и У2= 1—0,56=0,44.
|
|
|
= 1,3 |
|
•н |
|
[Gn = у |
Для получения плотного и достаточно пластичного в процессе укладки состава полимербетона необходимо, чтобы полимерная мастика заполнила все пустоты между зернами песка и щебня и раздвинула их на размер, равный средней крупности зерен наполнителя (муки); 1 ч. по массе полимерной мастики может заполнить пустоты песка, взятого в следующем количестве:
1 1/Рн + mCB/m,
П Vn + a
Где G„ — расчетное количество песка, кг; у'п — насыпная плотность песка, уд = 1,3 ... 1,4 кг/л, рн — плотность наполнителя, кг/см3; гпв — масса связующего и наполнителя, кг; Vn — объем пустот в песке, Vn = 0,4; а — коэффициент удобоукладываемости, а «0,5.
Таким образом, для получения плотного полимербетона с двумя фракциями щебня 1 ч по массе мастики и примерно 1,12 ч. по массе песка должны заполнить 44% пустот, образованных щебнем, т. е. 21% мастики и 23% песка.
При рассмотрении реальных систем неправильная геометрическая форма зерен заполнителей, их шероховатость, образование в процессе укладки сводов или сот значительно искажают картину и влияют на плотность упаковки. К этому необходимо добавить влияние краевого эффекта, так как в отличие от геометрической модели с бесконечной укладкой шаров реальные конструкции имеют вполне определенные размеры. В этом случае вокруг основных зерен заполнителя, граничащих с плоскостью опалубки или оснастки, группируется меньшее число зерен, эквивалентных соответствующим пустотам, или размеры этих пустот отличаются от размеров пустот в объеме изделия. Все эти отклонения практически не поддаются математической обработке. Поэтому закономерности, справедливые для идеальных систем, были приняты нами в качестве исходных. При подборе оптимальных составов полимербетонов все величины экспериментально уточнялись.
Для уточнения оптимального состава заполнителей по наибольшей плотности в сухом состоянии был использован достаточно простой и надежный способ, разработанный в Белорусском политехническом институте и несколько модернизированный в НИИЖБ.
Фракционированный подбор заполнителей производится в специальном приборе, предназначенном для этих целей. ■
Прибор представляет собой съемный цилиндр 3, укрепленный на основании 6 (рис. 16) с внутренним диаметром цилиндра 160 и высотой 400 мм. В направляющей втулке 2, смонтированной на двух стойках 4, свободно перемещается шток 1 с наглухо укрепленным диском 5. Шток имеет метрическую шкалу с ценой деления 1 мм; 10 мм по штоку соответствуют 200 см3 цилиндра. Весь прибор струбцинами крепится к плите лабораторного вибростола. По разности между суммой объемов до
смешивания и объемов, полученных после смешивания и виброуплотиепия, строится графих изменения плотности сухой смеси, который показывает, что максимальная плотность смеси получается при определенном соотношении крупной и мелкой фракции заполнителя. За постоянное значение принимают массу смеси двух ранее взятых фракций и к ней добавляют массу щебня следующей более мелкой фракции.
Таким образом, можно последовательно осуществить плотный подбор сухого состава заполнителей с любым количеством фракций. При этом необходимо иметь в виду, что на приборе с внутренним диаметром цилиндра 160 мм максимальный размер щебня не должен превышать 40 мм.
Как показали проведенные исследования, при получении составов с прерывистой гранулометрией основная трудоемкость падает на рассев мелкодисперсных фракций и определение их оптимального количества в смеси. При этом разница в размерах последующих и предыдущих зерен не выходит за пределы размеров стандартного набора сит, а эффект уплотнения по сравнению с эффектом уплотнения нерассеянных составов становится столь незначительным, что теряется смысл в таком фракционировании. Поэтому нами был принят способ подбора плотных составов полимербетонов с использованием «полупрерывистой гранулометрии», который предусматривает фракционирование одного лишь щебня и выбор соответствующего модуля крупности песка. Тонкомолотые добавки имеют непрерывную гранулометрию, т. е. они используются без рассева. Этим способом были подобраны плотные составы полимербетонов с расходом синтетической смолы от 7,5 до 8,5% (165—185 кг/м3) по массе наполнителей и заполнителей (табл. 14, 15) при ранее принятом расходе связующего от 220 до 240 кг/м3, а в некоторых случаях и до 320 кг/м3.
Проведенные исследования позволили разработать экспериментально-теоретический метод подбора оптимальных составов полимербетонов, который имеет следующие особенности. Составы полимербетонов проектируют в три стадии: вначале экспериментально определяют оптимальный состав клеящей мастики, затем теоретически вычисляют размеры щебня для состава бетона с «полупрерывистой гранулометрией», количество фракций и их соотношение между собой, после этого состав заполнителей уточняется на приборе для подбора сухой смеси.