ПОЛИЭТИЛЕН ВЫСОКОГО ДАВЛЕНИЯ

МОЛЕКУЛЯРНО-МАССОВОЕ РАСПРЕДЕЛЕНИЕ

Как было сказано выше, макромолекулы ПЭВД обладают характер­ной разветвленной структурой вследствие того, что условия радикальной, полимеризации этилена благоприятны для передачи цепи на полимер. Эти же реакции оказываются определяющими для формирования ММР ПЭВД.

Внутримолекулярная передача цепи посредством образования пере­ходного 6-членного кольца приводит к обрыву полимерной цепи (рас­щепление третичного радикала), происходящему достаточно часто, чтобы образовать большую фракцию полимера сравнительно малой молекуляр­ной массы. Поскольку именно эта реакция как основная реакция обрыва полимерной цепи (см. гл. 4) определяет величину Мп, то последняя ока­зывается сравнительно малой (1 • 104-5 • 104).

Межмолекулярная передача цепи на полимер, а также возможная внут­римолекулярная передача цепи далее, чем на 5-й атом С макрорадикала, вызывают многократное возобновление роста макромолекулы. Рост осу­ществляется путем образования длинных боковых ветвей, сравнимых по молекулярной массе с Мп, ибо их длина также определяется реакцией расщепления третичного радикала. Вероятность возникновения длинных боковых ветвей определяется, с одной стороны, размером мертвой мак­ромолекулы (или макрорадикала), на которую передается цепь, а с дру­гой стороны, концентрацией полимера в реакционной смеси: она увели­чивается и с ростом макромолекулы, и с ростом концентрации. Поэтому образование длинных ветвей — процесс самоускоряющийся, приводящий к образованию больших, сформированных из отрезков-ветвей макромо­лекул, молекулярная масса которых в десятки и сотни раз превосходит Мп, и, следовательно, обеспечивающий большую полидисперсность ПЭВД по молекулярной массе.

Попытки описать характер ММР и разветвленность ПЭВД, исходя из кинетических особенностей радикальной полимеризации этилена, пред­принимались многими авторами. Обзор этих работ можно найти, напри­мер, в [38, 104, 112]. Остановимся на их основных чертах.

Впервые ММР продукта радикальной полимеризации с многократной передачей цепи на полимер в применении к полиэтилену рассмотрел Вис­ли [58, с. 445]. Это рассмотрение относится к проведению непрерывного процесса полимеризации в реакторе автоклавного типа. Введя в уравне­ние кинетики полимеризации параметр ДЦР |3, равный вероятности однократного разветвления среднечисленной цепочки с молекулярной массой Мп о, он получил функцию распределения, названного его именем:

<?„(М) = а/(1 + а/ЗМ) 1 + 1/(3. (7.7)

Средние значения молекулярной массы связаны с параметрами а и (3 уравнениями:

М„ = 1/а(1-(5); Mw = 2ja(\ — 20) .

Отсюда следует, что а = 1 /Мп0.

Функция Бисли предсказывает ММР, характеризующееся высокомо­лекулярным „хвостом" и большими значениями отношения Mw/Mn, од­нозначно определяющимися величиной (3:

Mw/Mn = 2(1 - (3) / (1 — 2(3) .

В работе [112, с. 154] показано, что функция (7.7) может быть по­лучена из обобщенной леммы о равновесном распределении живых це­пей, если принять, что эффективная скорость роста цепей возрастает с М, что справедливо для случая многократной передачи цепи на полимер, и что при таком рассмотрении безразлично, возникали и росли ветви по­следовательно друг за другом (цепь прекращала рост, а затем активиро - * валась и вновь росла) или одновременно (самоускоряющийся рост).

Распределение, полученное Бисли, близко к таковому Бэмфорда и Томпа [36, с. 298]. Решив задачу нахождения относительного содержа­ния многократно разветвленных фракций, образовавшихся в подобном процессе полимеризации, Бэмфорд и Томпа получили распределение, ко­торое с хорошим приближением может быть описано следующим уравне­нием [112, с. 153]:

Qn(M) = ae-aMll-p+a0M+0(a0M)1IP]/[l - (а/3М)1].

Расчеты Бисли получили дальнейшее развитие в работе [113], осно­ванной на реалистической модели кинетики радикальной полимеризации зтилена, учитывающей все реакции молекулярного обрыва.

В последние годы получили развитие статистические методы расчета функций ММР ПЭВД. В работе [114] проведен расчет моментов ММР, но при этом не учтено Д-расщепление третичного радикала. В работе [115] на основании теории ветвящихся процессов рассчитаны мгновенные зна­чения ММР с учетом ДЦР и КЦР.

В работах [105] предложен новый подход к определению моментов( ММР разветвленных полимеров в терминах вероятностей роста основной Цепи и образования боковых ветвей. В модели подразумевается гребне­образное строение полимера, но авторы и другие исследователи [107, 116] применили такой подход к ПЭВД. Далее предложенная модель изу­чена методом производящих функций и получены аналитические выра­жения для численной функции распределения и моментов ММР [106].

Кинетическая схема полимеризации не конкретизируется ни в [107], нив [106].

Разветвленность макромолекул, широкое ММР, связанная с высокой і степенью кристалличности нерастворимость ПЭВД в органических раст­ворителях при температуре ниже 80 °С весьма затрудняют, а иногда и де­лают невозможным определение молекулярной массы этого полимера методами, успешно применяемыми к другим полимерам [84]. Так, наличие низкомолекулярных фракций искажает результат определения Мп методом осмометрии, завышая его вследствие диффузии полимера через мембрану. Присутствие даже весьма незначительной доли очень больших полимерных частиц, так называемого „микрогеля", не позволя­ет правильно определить Mw методом светорассеяния.

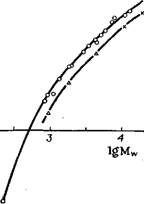
Широко используемый метод определения молекулярной массы по характеристической вязкости [г?] неприменим для ПЭВД как для раз­ветвленного полимера, поскольку [г?] является функцией не только мо­лекулярной массы, но и разветвленности, а связь между этими двумя характеристиками обычно заранее не известна. Кроме того, нельзя реко­мендовать определение молекулярной массы ПЭВД по [г?], так как зави­симость [г?] от М на протяжении большого интервала значений М очень слаба или даже исчезает с ростом М (см. рис. 7.9). Исключение здесь со­ставляет область малых значений М, соответствующая фракциям ПЭВД, не содержащим макромолекул с длинными ветвями. На рис. 7.10 пред­ставлена в логарифмическом масштабе зависимость [г?] образцов неболь­шой полидисперсности в различных по термодинамическому качеству растворителях от Mw в интервале значений молекулярной массы от 100 до 20000 [117]. В области • 103 зависимость [17] от М линейна и описывается следующими соотношениями.

Внонане при 110°С: [т?]=4,40 • 10_5М-5,63 • Ю-3 дл/г.

В декалине при 135 °С: [т?] = 4,10 • 10"sM-8,40- Ю-3 дл/г.

В «-ксилоле при 85 °С: [17] = 3,33 • 10"sM-5,30- 10"3 дл/г.

Эти данные могут быть использованы для определения средневязко - стной молекулярной массы Мц низкомолекулярных образцов полиэти­лена (воски, фракции полидисперсных образцов).

В 50-х-60-х годах сведения о ММР ПЭВД получали с помощью пре­паративного фракционирования с последующим определением молеку­лярных масс фракций. Проведение фракционирования при температуре выше температуры кристаллизации полимера в растворе и выделение достаточно большого числа (не менее 20) фракций обеспечивает удовлет­ворительное фракционирование ПЭВД по молекулярной массе, а отсут­ствие большой полидисперсности позволяет избежать ошибок в опреде­лении молекулярной массы фракций названными выше методами. Все зто является залогом успешного определения ММР ПЭВД с помощью фракционирования, однако длительность и трудоемкость анализа делают нежелательным применение этого метода.

Рис. 7.10. Зависимость lg [17] от lgМ для об - \6\tf\ разцов полиэтилена малой полидисперсно - д

Сти в различных растворителях: о — декалин, 135°С; Д — 1-бромнафталин, 110°С; X — дифениловый эфир, 161,4°С (©-растворитель)

В настоящее время для определе - j ния ММР, а попутно и ДЦР, ПЭВД обычно используют сочетание данных аналитического экспресс-фракциони­рования (ГПХ, скоростная седимен­тация) и результата определения сред - _2 _ ней характеристики массы или разме­ра макромолекул исследуемого поли­дисперсного образца, например [17], с последующей обработкой данных анализа с помощью ЭВМ или сочетание _ j. данных двух разных методов экспресс - фракционирования [110, 111; 118, с. 283]. Все зти способы анализа мо­лекулярной структуры в той или иной мере используют модельные пред­ставления о влиянии разветвленности на размеры и массу макромолеку­лы и являются косвенными методами. Остановимся на одном из них.

Наиболее распространенный метод характеристики разветвленного полимера по молекулярной массе и разветвленности — метод ГПХ в со­четании с характеристической вязкостью исходного образца требует предварительных сведений о связи между числом узлов ветвления в мак­ромолекуле и ее молекулярной массой, т = f{M). Полидисперсность по­лимера по молекулярной массе может сопровождаться и полидисперсно­стью по степени разветвленности, характеризуемой отношением \ = т/М, однако в программах расчета параметров ММР и разветвленности ПЭВД по данным ГПХ и [г?] обычно используют линейное соотношение между т и М, т. е. априори предполагается независимость частоты узлов ДЦР от М, Х = const.

Кроме того, при таком рассмотрении обычно не разделяют эффектов КЦР и ДЦР, считая вклад КЦР в общий эффект уменьшения размера раз­ветвленной макромолекулы по сравнению с линейным изомером пренеб­режимо малым. Но если предположение о пренебрежимой малости вкла­да КЦР несправедливо, то величина X лишается физического смысла: она Уже не характеризует ДЦР, но не характеризует и суммарного эффекта разветвленности, поскольку найдена способом, справедливым только Для ДЦР. В работе [119] рассмотрены последствия предположения, что Х = const, и неучета вклада КЦР при анализе ПЭВД этим методом. Рассмот­рение проведено для образца, обладающего 2,2 короткими бутильными ветвями на 100 углеродных атомов и характеризующегося зависимостя-
ми: т~М, т~М°'&, т~М1>2. Фактору описывался соотношениями gn =ge {т), где є = 0,5 - 1,5, =/z3 (т).

Оказалось, что исключение эффекта КЦР не влияет на значение Мп и приводит к уменьшению Mw, а следовательно, и Mw/Mn, на 10-20%, а также к слабому уменьшению отношения Mz/Mw. Значение X при этом уменьшается более существенно: в 1,8-1,5 раза. При этом увеличение значения є усиливает влияние эффекта КЦР на определение М и умень - - шает — на определение т.

Росту экспонента в соотношении т ~ М соответствует снижение сред - нечисленных значений величин М и т и повышение более высоких сред­них значений их, т. е. возрастание полидисперсности по М и т. При этом увеличение полидисперсности по т более существенно, чем по М: в зави­симости от показателя степени є отношение Mw/Mn увеличивается в 1,2— 1,6 раза, a mwlmn — в 3,7—8,6 раза.

Соотношение между средними значениями величины X при \Фconst соответствует тенденции изменения X с изменением М. Значение X, най­денное в предположении т~М, лежит между средними значениями Хш и Хг, найденными при \Фconst.