ПОДГОТОВИТЕЛЬНЫЕ ПРОЦЕССЫ ОБОГАЩЕНИЯ

ДРОБЛЕНИЕ

ТЕМА 5 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЦЕССА РАЗРУШЕНИЯ ГОРНЫХ ПОРОД

1. Способы разрушения горных пород при дроблении и измельчении.

2. Свойства горных пород, имеющие значение при разрушении.

3. Стадии дробления. Степень дробления.

4. Гипотезы дробления и измельчения.

Процессы дробления и измельчения применяются для доведения материала до необходимой крупности, гранулометрического состава или заданной степени раскрытия минералов, т. е. для получения свободных минеральных зерен. При этом куски горных пород разрушаются внешними силами. Разрушение – это процесс зарождения и роста трещин и пор. Происходит по ослабленным сечениям, имеющим трещиноватости или другие дефекты структуры. Разрушение наступает после перехода за предел прочности нормальных и касательных напряжений, возникающих в материале при его упругих деформациях: сжатии, растяжении, изгибе или сдвиге. Предел прочности – предельное значение напряжения, выше которого образец разрушается практически мгновенно, а ниже – живет неограниченно долго.

Различные способы дробления и измельчения отличаются видом основной необратимой деформации, вызвавшей разрушение. В соответствии с этим способы разрушения делятся на (рис. 2.1):

1) раздавливание – наступает после перехода напряжений за предел прочности на сжатие;

2) раскалывание – после перехода напряжений за предел прочности на растяжение;

3) излом - после перехода напряжений за предел прочности на изгиб;

4) срезывание - после перехода напряжений за предел прочности на сдвиг;

5) истирание - после перехода напряжений во внешних слоях кусков за предел прочности на сдвиг;

6) удар – воздействие динамических нагрузок на материал, деформации возникают те же: сжатие, растяжение, изгиб, сдвиг.

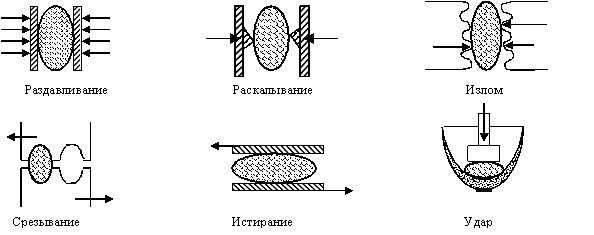Рисунок 2.1 – Способы разрушения материалов

Эти способы разрушения являются общими и для операций дробления, и для операций измельчения, однако эти процессы различаются по своему технологическому назначению. Принято считать дроблением такой процесс разрушения, в результате которого большая часть продукта имеет крупность выше 5 мм. При измельчении получают продукт мельче 5 мм. Размер 5 мм принят условно.

Все машины, применяемые для разрушения кусков горных пород делятся по технологическому назначению на дробилки и мельницы. Отличительными особенностями этих типов машин являются:

Дробилки – 1) между дробящими телами всегда есть зазор, который свободен на холостом ходу и заполнен материалом на рабочем ходу; 2) выдают в основном кусковой продукт с преобладанием крупных фракций.

Мельницы – 1) измельчающие детали соприкасаются на холостом ходу, а на рабочем – разделены слоем материала; 2) выдают порошкообразный продукт с преобладанием мелких фракций.

В различных конструкциях машин могут использоваться сразу несколько способов разрушения, но преобладающим является один из них:

- раздавливание – в щековых, валковых и конусных дробилках;

- раскалывание – в зубчатых и игольчатых дробилках;

- удар – в молотковых дробилках и дезынтеграторах;

- истирание – в мельницах.

Для процессов разрушения наиболее важны прочность (крепость), дробимость, измельчаемость и абразивность горных пород. Прочность – способность твердого тела сопротивляться разрушению от действия внешних сил. Характеризуется предельными напряжениями, которые могут быть созданы в опасном сечении тела.

С точки зрения физико-механических свойств пород наиболее выгодно разрушать их растяжением. Но по конструктивным соображениям в основном используется раздавливание. Поэтому для сравнения прочностных свойств пород используют напряжение на сжатие или коэффициент крепости, разработанный проф. Протодьяконовым М. М. По шкале Протодьяконова все породы делятся на 10 категорий с коэффициентами крепости от 0.3 для самых слабых до 20 для наиболее прочных пород.

Дробимость – это обобщающий параметр для многих механических свойств пород и выражает энергоемкость процесса дробления.

Измельчаемость оценивают по удельной производительности мельницы по вновь образованному расчетному классу.

Абразивность оценивают по износу материала рабочих поверхностей машин в процессе дробления (измельчения) при трении.

Оценка результатов дробления (измельчения) производится по степени дробления (измельчения) и эффективности работы машин. Степень дробления – отношение размеров кусков исходного материала к размеру кусков продукта дробления.

I = D / d, (2.1)

Где i – степень дробления, D, d – средний или максимальный размер куска в питании и дробленом продукте, соответственно.

Нет таких дробильных машин, которые могли бы принимать исходную руду и выдавать конечный продукт. Поэтому применяют несколько приемов (стадий) дробления (см. схему). В зависимости от крупности исходного и дробленого материала различают следующие стадии дробления и измельчения, показатели для которых приведены в табл. 2.1.

Таблица 2.1 – Стадии дробления и измельчения

При дроблении (измельчении) в несколько последовательных стадий общая степень дробления (измельчения) определяется как произведение всех степеней дробления в отдельных стадиях:

I = i 1• i 2 • i 3 • i n. (2.2)

Дробилки (мельницы) могут работать в открытом или замкнутом цикле. При открытом цикле материал проходит дробилку один раз, при замкнутом - надрешетный продукт грохота непрерывно возвращается в дробилку на додрабливание, образуя циркулирующую нагрузку. В случае мельниц – пески (крупный продукт) гидроциклона или классификатора возвращаются на доизмельчение. Замкнутые циклы обеспечивают более высокую степень дробления (измельчения) по сравнению с открытыми.

Если продукт дробления представляет собой свободные зерна полезного минерала, то дальнейшее дробление не имеет смысла, т. к. будет только приводить к переизмельчению материала. Процесс является энергоемким, поэтому проф. Г. О. Чечет сформулировал принцип НЕ ДРОБИТЬ НИЧЕГО ЛИШНЕГО. При разрушении происходит преодоление сил сцепления между частицами и образование новой поверхности. Энергия, потребляемая при дроблении (измельчении) расходуется на: 1) упругую деформацию разрушаемых зерен, т. е. рассеивается в окружающее пространство в виде тепла; 2) образование новой поверхности, т. е. превращается в свободную поверхностную энергию измельченных зерен. При измельчении расход полезной энергии – на образование новой поверхности – составляет около 1% общего ее расхода.

Пусть разрушается зерно в виде куба с размером d, представленное на рис. 2.2.

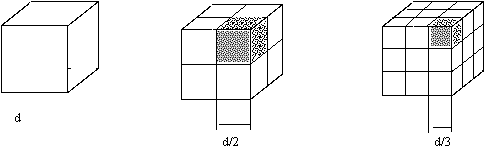Рисунок 2.2 – Изменение суммарной поверхности зерен при дроблении

Тогда поверхность частиц будет:

До дробления: S 1 = 6• d 2 •1 Кубик. (2.3)

После дробления: S 2 = 6 • ( d / 2 ) 2 •8 Кубиков = 6 d 2 •2; (2.4)

S 3 = 6 ( d / 3 ) 2 •27 = 6 d 2 •3; (2.5)

…………………..; (2.6)

S n = 6 d 2 •n. (2.7)

Здесь n – количество частиц.

Таким образом, при уменьшении размеров кусков руды происходит увеличение общей поверхности частиц.

Для оценки порошкообразных материалов используется понятие удельной поверхности, т. е. поверхности, приходящейся на единицу веса материала. В данном случае:

S yд = 6 d 2 / d 3 δ = 6 /d δ . (2.8)

Обозначим 6 / δ = К. Для частиц малого размера К = соnst.

При дроблении Q весовых единиц материала со средним размером кусков D получим столько же весовых единиц материала со средним размером d. Поверхность материала до дробления:

S 1 yд = K Q / D. (2.9)

После дробления:

S 2 yд = K Q / d. (2.10)

Вновь образованная при дроблении поверхность будет:

ΔS = S 2 – S 1 = K Q / d – K Q / D = K ( 1 / d – 1 / D ) Q (2.11)

Известно несколько гипотез энергетической оценки процессов дробления и измельчения. Одна из них – гипотеза Риттингера (1867г): Расход энергии на дробление пропорционален величине вновь образованной поверхности. В математическом выражении имеет вид:

E = K 0 ΔS = K 0 К ( 1 / d – 1 / D) Q. (2.12)

Здесь E – расход энергии, K 0 – коэффициент пропорциональности, по физическому смыслу представляет собой расход энергии на образование одной квадратной единицы новой поверхности.

Обозначим: Ko K = K1 . (2.13)

Тогда E = K1 ( 1/d – 1/D ) Q. (2.14)

Умножим и разделим правую часть уравнения (2.14) на D, получим

E = K1 ( 1/d – 1/D ) Q • D/ D = K1 ( D /d – D /D ) Q / D = K1 ( i – 1 ) Q / D. (2.15)

Таким образом, по Риттингеру расход энергии на дробление одной весовой единицы материала пропорционален степени дробления i минус единица.

По гипотезе Кирпичева (1874г.) и Кика (1885г.) энергия, необходимая для дробления и измельчения материала пропорциональна его весу (или объему):

E1 = K0 Q. (2.16)

Из выражения (2.16) следует, что затрачиваемая энергия не зависит от крупности материала. Коэффициент Ко выражает расход энергии на единицу веса при данной степени измельчения. Можно выбрать схему с одинаковыми степенями дробления в каждой стадии:

I 1 = i 2 = i 3 = …..= i n. (2.17)

Тогда с учетом (2.17) общая степень дробления составит:

I = i n, (2.18)

Где n – число стадий дробления.

При этом энергии дробления в каждой стадии будут равны между собой:

E 1 = E 2 = E 3 . (2.19)

С учетом выражений (2.16) и (2.19) общая энергия дробления по всей схеме будет:

E = K0 Q • n. (2.20)

Для исключения степени в выражении (2.18) выполним его логарифмирование и выразим n:

Lg I = n lg i, (2.21)

N = lg I / lg i (2.22)

Подставим соотношение (2.22) в формулу (2.20) и получим:

E = K0 Q lg I / lg i. (2.23)

Для одного и того же материала и при одной и той же степени дробления в каждой стадии величины К0 и i будут постоянными, поэтому можно обозначить

K2 = K0 / lg I, (2.24)

Тогда энергия дробления (измельчения) определится с учетом соотношения (2.23) как:

E = K2 Q lg I, (2.25)

Математическое выражение для степени дробления (2.1) можно представить в виде

D / d = (1/d) / (1/D). (2.26)

Тогда

Lg I = lg [ ( 1/d ) / ( 1 / D )] = lg ( 1 / d ) – lg ( 1 / D ). (2.27)

С учетом соотношений (2.25) и (2.27) выражение для энергии дробления будет иметь вид:

E = K2 [ lg ( 1 / d ) – lg ( 1 / D ) ] Q. (2.28)

Формула (2.28) представляет собой математическое выражение гипотезы Кика-Кирпичева аналогично выражению гипотезы Риттингера. По Риттингеру расход энергии пропорционален поверхности, по Кику-Кирпичеву – объему. Соответственно эти законы носят название поверхностного и объемного законов дробления (измельчения). Данные экспериментов и промышленной практики показали, что эти законы справедливы лишь в определенных диапазонах крупности. Гипотеза Риттингера хорошо согласуется с практикой при тонком измельчении, а гипотеза Кика-Кирпичева – при крупном дроблении.

Академик Ребиндер (1941г.) предложил гипотезу, охватывающую любой случай разрушения полезных ископаемых, математическое выражение которой имеет вид:

A = σ ΔS + K ΔV. (2.29)

Здесь A – работа, затрачиваемая на разрушение твердого тела, σ – поверхностная энергия на единицу твердой поверхности (σ - избыток свободной энергии в пограничном слое), ΔS – поверхность, вновь образуемая при разрушении, ΔV – часть объема тела, подвергшаяся деформации, K – работа упругой и пластической деформации, приходящаяся на единицу объема.

При крупном дроблении больших кусков руды K ΔV >> σ ΔS, т. к. приращение поверхности незначительно, и работа будет в основном пропорциональна объему (гипотеза Кирпичева):

AK ≈ K ΔV = КK D 3. (2.30)

При разрушении мелких кусков руды (измельчение) σ ΔS >> K ΔV, т. к. приращение поверхности значительно. При этом работа почти пропорциональна величине новой образованной поверхности (гипотеза Риттингера):

AR ≈ σ ΔS = KR D 2. (2.31)

Гипотеза Ребиндера связывает процесс разрушения с физико-механическими свойствами пород и минералов (поверхностная энергия, твердость).

Разделим обе части уравнения (2.29) на ΔS и получим:

A / ΔS = σ ΔS / ΔS + K ΔV / ΔS, (2.32)

Отсюда

A / ΔS = σ + K ΔV / ΔS. (2.33)

Обозначим в выражении (2.33):

σ + K ΔV / ΔS = H s . (2.34)

Тогда с учетом соотношений (2.33) и (2.34) получим:

H s = A / ΔS. (2.35)

Величину H s надо рассматривать как коэффициент твердости, равный работе образования единицы новой поверхности. Вместе с тем величина H s связана с поверхностной энергией соотношением (2.34). Таким образом, чем больше поверхностная энергия твердого тела, тем больше его твердость, а, следовательно, и больше работа, которую надо затратить на разрушение – образование новой поверхности.

Гипотеза Ребиндера пригодна для любого диапазона крупности, т. к. она сводится к закону Риттингера или Кирпичева при определенных значениях крупности. Эта гипотеза учитывает оба вида энергии – поверхностную и потенциальную энергию деформации в объеме дробимого тела.

Американский ученый Бонд (1950г.) предложил гипотезу, промежуточную по отношению к законам Риттингера и Кирпичева:

По гипотезе Бонда элементарная работа пропорциональна приращению параметра, являющегося среднегеометрическим между объемом и поверхностью :

(2.38)

Практика показывает определенную связь между индексом работы по Бонду и коэффициентом крепости пород по Протодьяконову.