ОТОПЛЕНИЕ И ВЕНТИЛЯЦИЯ

ВОЗДУХОВОДЫ РАВНОМЕРНОЙ РАЗДАЧИ И РАВНОМЕРНОГО ВСАСЫВАНИЯ

Воздуховоды равномерной по длине раздачи и равномерного по длине всасывания находят в технике широкое применение. Приточные воздуховоды, подающие воздух равномерно по длине, применяют в воз-

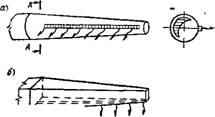
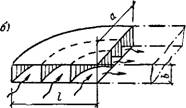
Рис. XI.13. Воздуховод равномерной раздачи посто­янного поперечного сечения с переменными по дли­не размерами отверстий

А — общий вид воздуховода: 1 — n — номера отверстий: If—f N—площади отверстий; б — направление движения

Воздуха из отверстий; в — направление движения воздуха при устройстве внешнего экрана

4 -4 і і. і f/t-f

1 2 "і ТТ fj-i N

Душных завесах, для сдувания вредных вы­делений с поверхности испарения, для раз­дачи воздуха в помещениях. Вытяжные воз­духоводы, удаляющие воздух равномерно по длине, применяют в местных и бортовых отсосах и других вентиляционных и техно­логических устройствах. Термин «равномер­ность» предполагает линейную зависимость ном сечении воздуховода от его длины.

Равномерную раздачу воздуха можно техническими приемами.

Наиболее часто применяют воздуховоды постоянного поперечного сечения с переменной по длине площадью отверстий или щелей в стен­ках для выхода воздуха (рис. XI. 13,а). Другая разновидность — возду­ховоды переменного сечения с одинаковыми по длине отверстиями или щелями для выхода воздуха.

Конструктивное оформление отверстий и щелей в стенках возду­ховода весьма разнообразно. Самое простое устройство для выхода воз­духа — это поперечная или продольная щель в стенке воздуховода либо отверстие с острыми краями. Недостатком такого устройства является неоднородность струй воздуха по скорости и направлению (рис. XI.13, б). Иногда возможно налипание струй, выходящих из щелей или отвер­стий, на наружную поверхность воздуховода. В этом случае воздуховод равномерной раздачи создает в помещении весьма неравномерные пото­ки. Простейшим устройством, направляющим струи и препятствующим налипанию их на воздуховод, является внешний экран (рис. XI. 13,в). Для этой же цели служат различные направляющие решетки, козырьки и внутренние экраны. Хорошие результаты дает раздача воздуха через мелкие круглые или прямоугольные отверстия — перфорацию. Перфори­рованные воздуховоды широко применяют на практике.

При расчете воздуховодов равномерной раздачи принимают сле­дующие допущения: коэффициенты местного сопротивления выхода для отверстий или щелей постоянны по длине воздуховода, сопротивление движению воздуха по воздуховоду создается трением (местное сопро­тивление при делении потока не учитывается).

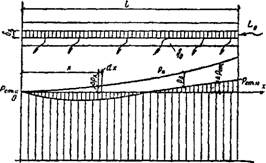
Рассмотрим схему давлений в приточном воздуховоде равномер­ной раздачи при постоянном сечении его (рис. XI.14). Предположим, что число отверстий очень велико, и можно считать, что они составля­ют сплошное продольное отверстие высотой 6х-

Статическое давление в конце воздуховода при х=0

Р^ЗЫХ

Рст. к = £вых --------------------------------------------------------------------------- • (X* •78)

Динамическое давление в этом сечении равно нулю, так как рас­ход в направлении х отсутствует. Следовательно, полное давление Раж в этом сечении равно статическому.

Рис. XIЛ 4. Распределение дав­лений по длине воздуховода равномерной раздачи

Рп, Рст, Рд — соответственно пол­ное, статическое и динамическое давление по длине воздуховода; I — дайна воздуховода; fo— пло­щадь воздуховода; l0 расход воздуха через воздуховод

В произвольном сечении х изменение полного давления определя­ется потерями давления на трение:

Dx

D (Дрх) = Яхр —Рях, (XI. 79)

Где ХТр — коэффициент сопротивления трения; d — диаметр круглого воздуховода или эквивалентный по скорости диаметр прямоугольного воздуховода; рд* — динами­ческое давление в сечении х, определяемое по формуле

/ lq yjl

РдХ ~ fo1 1 2

Или

Рд* - - = *2РдЬ (XI.80)

Где L — расход воздуха на 1 м воздуховода; рді — динамическое давление в се­чении воздуховода при х~1 м.

Проинтегрируем выражение (ХЇ.79), предположив режим движе­ния соответствующим гидравлически шероховатым воздуховодам:

Дрх = Яхр-^-рді. (XI.81)

При этом постоянная интегрирования равна нулю.

Полное давление в воздуховоде в произвольном сечении х:

Рп* = рст. к+др*. (XI. 82)

Количество воздуха, выходящего через отверстие в боковой стен­ке воздуховода, определяется значением статического давления:

Рстл - = Ршг — Рдлг, (XI. 83)

ИЛИ

Рстх = Рст. к + —~ Рді — *2рді. (XI. 84)

Следовательно, величина рстх изменяется по длине воздуховода. Ана­лиз этой функции при произвольных значениях аргумента xjl>0, в том числе при x(l= 1, показал наличие экстремальной точки, в которой рстх принимает минимальное значение. Конфигурация кривой рстх по­казана на рис. XI.14.

Значение рст. к, которое определяется скоростью выхода воз-духа и коэффициентам местного сопротивления отверстия [формула (XI.78)],

Рис XJ.15. График изменения Дрст* по длине воздуховода равномерной раздачи при постоянном сечении его 1 — при ATp=const; 2 — при ЛТр (Re)

Можно ^принять за условный нуль. Тогда изменение статического дав­ления по длине воздуховода будет определять величина

Д ___________ ____ 2 I ^тр

&РсТХ— Рстх Рст-к — Рді Х 1

(XI. 85)

Эту формулу можно записать в обобщенном виде, если ввести аргу­мент х:

^Рстх — ^ »

Где Дрстх — обобщенное изменение статического давления по длине воздуховода, равное

Арст-г / Ятр 4 2

Ьрстх — '

Рді

Х — обобщенная абсцисса, равная

Згі/Рцф *

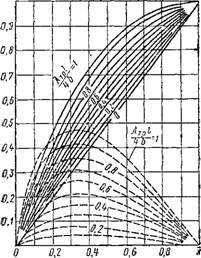
На рис. XI. 15 представлен график изменения Лрстх по длине возду­ховода равномерной раздачи при постоянном сечении его. Характерна конфигурация кривой.

Для «коротких» воздуховодов, когда х<. 1 (л;<Зс? Дтр), статическое давление в начале воздуховода меньше, чем в его конце (при х==0). При этом на расстоянии х=2/3 от конца воздуховода наблюдается мини­мальное статическое _давление (АрСт =—0,148). Для «протяженных» воздуховодов, когда х> (x>3d/XTP), статическое давление в начале воздуховода больше рст. к и при увеличении его длины резко возрастает.

При выводе формул (XI.86) — (ХІ.88) не учитывалась зависимость Хтр от v и, следовательно, от х. Это справедливо лишь для режима дви­жения, соответствующего гидравлически шероховатым воздуховодам.

Аналогичный результат можно получить для режима движения, соответствующего гидравлически гладким воздуховодам, с учетом из­вестной зависимости, справедливой Для Re^ll d/K'-

Я________________________________________ d_

~~ Re0'25 '

Формула (XI.84) для этого режима движения принимает вид

2 75

Рстх — Рст-к + Яг * ш Рді — X2 Рдъ (Х1 • 89)

А формулы (XI.86) — (XI.88) соответственно

Лрс™ = *2,75-*2; (XI. 90)

* (XI. 92)

2,75d/Яр

Здесь Яг — коэффициент сопротивления трения воздуховода

Зависимость (XI.90) представлена на рис. XI.15 пунктирной ли­нией.

Расчет воздуховода равномерной раздачи при постоянном сечении его проводят в такой последовательности.

1. Определяют, расход воздуха через одно отверстие или на 1 м длины воздуховода:

Т, А)

Или 1^ = — .

Определяют величину рдь

2. Вычисляют статическое давление в конце воздуховода по фор­муле (XI.78) при заданном значении Рбыху-

3. Определяют режим движения воздуха и распределение стати­ческого давления вдоль воздуховода ио формуле (XI.84) (для области гидравлически шероховатых груб и переходной) или по формуле (XI.89) (для области гидравлически гладких труб).

Величину pax можно определить также по графику на рис. XI.15.

4. Определяют площадь отверстий по одной из следующих формул:

F _ (^вых Р у»

N 2рстх J

Или

Ь = ТГ1- (ir—) ~ (XI.93)

Л^вых 2р,

Или ширину щели в сечении XI

С L0 /£вых р

(XI. 94)

I 2рс

Примечание Определение f можно проводить не для каждого отверстия, а для группы их, разбив воздуховод по длине на четыре — десять участков в зависимо­сти от его протяженности.

Пример XI.4. Рассчитать воздуховод равномерной раздачи при постоянном по­перечном сечении (200X600 мм) с выпуском воздуха через щель переменной по длине ширины.

Расход приточного воздуха Lo = 4000 м3/ч, длина воздуховода 1=5 м Абсолют­ная шероховатость стенок воздуховода /С=0,1 мм. Скорость на выходе иВых=8 м/с, КОЭффИЦИеНТ МеСТНОГО СОПрОТИВЛеНИЯ ВЫХОДа £вых = 2,6 (Цвых=0,62)

Решение. 1. Расход воздуха на 1 м длины воздуховода

4000

1 = збоо1 = 0'222 м3/(с'м)-

Значение

Р / Lj 2 1,2 / 0,222 а

Рлі= —М =—— --------------------------------------------- 1------ =2,05 Па

2 f ) 2 0,2-0,6 /

2 Статическое давление в конце воздуховода по формуле (XI.78):

1 2-82

Рстк = 2.6 —---------------------------------------------- = ">8 Па-

3. Определяем режим движения: средняя по длине воздуховода скорость движения воздуха

4000-2,5

3600-5-0,2-0,6

Эквивалентным диаметр

2-0,2-0,6 dv = = 0,3 м (300 мм);

0,2 + 0,6

Фактическое значение критерия Рейнольдса

4,63-0,3 Re - .„ , _L6 = 0,09-106;

15,6-10"

Критическое значение

300

11 — = 33 000 < Re;

Следовательно, режим движения соответствует переходной или гидравлически шерохо­ватой области.

Коэффициент сопротивления трения для средней вдоль воздуховода скорости по формуле А. Д. Альтшуля.

О 1,25 + -0,02.

^0,09-10® 300/

Определяем рстх по формуле (XI.84) при разных значениях х- Результаты заносим в табл. XI.6.

Таблица XI.6

Расчет к примеру Х1.4

6„, м

4. Определяем 6-е по формуле (XI.94), результаты расчетов также заносим в табл. XI.6.

Расчет воздуховода с постоянным по длине статическим давлением

Впервые был проведен проф. К. К - Баулиным. Искомой величиной в этом расчете является площадь поперечного сечения воздуховода, со­ответствующая условию dpnx=d(&px) (изменение динамического дав­ления на участке воздуховода равно потерям давления на этом участ­ке). Щель или отверстия для выпуска воздуха не изменяют своих раз­меров по длине, так как рСт = const.

Используя упомянутое выше условие, можно записать для возду­ховода с произвольной формой поперечного сечения (при площади его fx и периметре Пх):

Пх р / Lx 2 *тр ~7Г~ "7Г ( Т2-) dx = dP&x. (XI. 95)

4/ж 2 W* /

При равномерной раздаче воздуха справедлива зависимость

L

(XI. 96)

Поэтому равенство (ХІ.95) можно преобразовать в выражение

П У2 2xdx 2х2 f 'dx

-Тdx-^т - -—з— > <Х1-97>

4 /2 f2 g

Из которого получим дифференциальное уравнение для определения fx:

Fx-— Пх = 0. (XI.98)

X о

Это уравнение решено для частных случаев: воздуховод прямоугольного сечения (клинообразный) —К. К. Баулиным; воздуховод круглого сече­ния (конусообразный) — В. Н. Талиевым. Для клинообразного возду­ховода (рис. XI.16) Пх—2(ах--Ь); fx~axb f'x=a'xb, поэтому уравнение (XL98) можно преобразовать так:

V+ Йг——) + ■= (Х1.9ЭД

Х 4Ь х J 4 v

Интегрируя это уравнение и вводя вспомогательные функции, получим:

Ax = q>a0 + yb, (XI. 100

^тР 1 - і ' 1- _

Гдеф^-^0-** ; (XI. 101)

4 Ь J "

Х = х/1 (начало координат совпадает с конечным сечением воздуховода, в кото­ром азс=0).

На рис. XI. 17 представлена номограмма для расчета значений Ф и ij) при Ширина щели в данном случае определяется по до­

Пустимой скорости воздуха на выходе vnon-

6щ = т^-. (XI. 102)

Доп

Значение статического давления, постоянного по длине воздуховода:

Рст — ъвых п

Или

Р«=г-і(іУ2- <х,-103)

Раздача воздуха может быть организована также через попереч­ные щели или через перфорированную стенку (имеющую ширину Ь). При этом метод расчета размеров остается таким же.

Значение полного давления в начальном сечении воздуховода равно:

Рт - + Рл» - U. f + f (-£-)'. (XI. 104)

Пример XI.5. Рассчитать воздуховод с постоянным статическим давлением, если 1о=8000 м3/ч, размеры его в начальном сечении а<,ХЬ=0,5X0,7 м, длина /=3 м. Раз-

Рис. XI. 16. Клинообразный воздуховод прямоугольного сечения с постоянным статическим давлением

I, Ь — длина и высота воздуховода; а0 — на­чальная ширина воздуховода; La, va — соот­ветственно расход и скорость движения воз­духа в начальном сечении воздуховода; — ширина щели воздуховода

Рис. XI. 17. Номограмма для определе­ния коэффициентов ф (сплошные линии) и ф (пунктирные линии)

Дача воздуха осуществляется через продольную щель с отбортованными краями (р-вых —0,81; £выу = 1,5). Скорость воздуха на выходе 6 м/с. Решение. 1 Скорость воздуха в начальном сечении

L0 8000

V _------------------------------------------ 2— =-------------------- ------ 6 35 м/с

0 3600 а0Ь 3600-0,5-0,7

Эквивалентный Диаметр в начальном сечении

2-0,5-0,7

Dv = —------------------------------------------------------ = 0,584 м.

У 0,5 + 0,7

Число Рейнольдса

6,35-0,584 Re0 = ' ь = 240 000.

0 15,6-10~6

Коэффициент сопротивления трения по формуле А. Д. Альтшуля?

/ 68 , 0, 1о>25

ЯтР = 0,11--------------------------------------------------------------------- г ~ I =0,016.

Тр V 240 000 584/

2. Вспомогательная величина

АтР I 0,016-3

= ------------------------------------------------------------- = 0,017.

46 4-0,7

Результаты дальнейшего расчета сведены в табл. XI.7. Коэффициенты ф и ij) определены по номограмме на рис. XI.17. Искомая величина в сечениях через 0,5 м приведена в последней графе таблицы.

Таблица XL7

0

Z

Рис. XI. 18. Воздуховоды постоянного статического давления с линейно-изме­няющейся площадью поперечного сече­ния

А — конусообразный; б — клинообразный; в — прямоугольный с разделительной стенкой

Рис. XI.19. Прямоугольный воздуховод равномерного всасывания постоянного поперечного сечения со щелью перемен­ной ширины

В практике строительства находят широкое применение воздухо­воды приблизительно равномерной раздачи воздуха, поскольку для упрощения заготовительных и монтажных работ целесообразно допус­тить некоторую неравномерность раздачи воздуха по длине. Это — воздуховоды с постоянным поперечным сечением и одинаковыми от­верстиями для выпуска воздуха. Неравномерность раздачи можно оце­нить по кривым на рис. XI. 15. Хорошие результаты дают клино - и ко­нусообразные воздуховоды, у которых площадь поперечного сечения изменяется по длине линейно (рис. XI. 18). Применяются также и сту­пенчатые воздуховоды, у которых размеры поперечного сечения отдель­ных участков изменяются по длине скачкообразно или плавно (с ис­пользованием конфузоров).

Равномерное всасывание воздуха может осуществляться воздухо­водами различного конструктивного исполнения. Например, прямо­угольными (рис. XI. 19) или круглыми воздуховодами постоянного попе­речного сечения со щелью неременной ширины. Эти воздуховоды обес­печивают постоянство расхода воздуха по их длине, однако скорость входа воздуха непостоянна по длине щели. При необходимости обеспе­чения постоянства по длине и расхода и скорости применяют воздухо­воды переменного поперечного сечения с отверстием (щелью) постоян­ной ширины (рис. XI.20). Для выравнивания потока в эти воздуховоды встраивают рассечки разных конструкций. Назначение рассечек — вы - равиять сопротивления входу воздуха на различных участках возду­ховода, сохранив постоянство ширины отверстия для входа воздуха.

Рассмотрим принцип расчета воздуховода равномерного всасыва­
ния при постоянном прямоугольном сечении (см. рис. XI. 19). Выделим сечение х, в котором статическое давление (разрежение) равно рстх, а динамическое давление

( H 2 Р

Потери давления на трение до сечения х (потери на смешение потоков не учитываются) равны:

Х

-Г п

Артр = J ^тр Prx dx. (XI. 105)

О

Подставив значения периметра П0, площади поперечного сечения f0 и динамического давления рдх, выраженные через a, b и х, и проинтегри­ровав равенство (XI. 105) при условии ЯТр=const, получим:

Д а / L0 V Р *3 a + b /YT infil

Лртр-Ц— ]Т — — . (XI. 106)

Постоянная интегрирования равна нулю, так как при £=0 потери ЛрТр= =0. Статическое давление в сечении х можно определить, во-первых, как сумму Арвхх—о, ЛрТр и рдсс" во-вторых, через потери давления на входе в воздуховод через щель шириной 6Х:

Рувх*

Рстх = Свх-------------------------------------------------------------------------- jp- - (XI. 108)

С учетом выражений (XI. 106), (XI. 107) и (XI.108) можно записать уравнение

Ъвх 2 2 6 /0 ; 2 /2 ab f0 ; I2 2

Если учесть, что

f0 { Lq fo

/о; /в,' а v fo;

То уравнение (XI. 109), связывающее 8Х с х, можно записать в упрощен­ном виде:

Г ■ ІТР. у2 /VI пт

Ьвх ~ = £вхГ^І------------------------------- « х - (Ai. JJU)

Бї 6 b 6 о

Решение уравнения относительно 8Х дает

--------------------------------------------- , (XI.111)

—— X® ^^ Я-рр ЛГ* ^^ х^

60 6£вха26 ' 6£вх а3 £вха2

Здесь бо — начальный размер щели для входа воздуха в воздуховод; как правило, принимается б0 —Ь. Коэффициент местного сопротивле-

14___ АО* ния £вх обычно равен 1,5. При этих условиях выражение (XI.111) мож­но преобразовать так:

(XI. 112)

А / + а2

Максимальная скорость в щели при х=1 равна vBsi—L0l(lbi). Эта скорость не должна превышать допустимую для данного помещения скорость в щели. Полное давление (разрежение) в сечении х—1 для учета в аэродинамическом расчете всей системы равно рЛ=рСгі—рш-

Пример ХІ.6. Рассчитать воздуховод равномерного всасывания при постоянном по длине поперечном сечении и переменной по длине ширине щели. Сечение воздухово­да 800X800 мм, длина / = 5 м, расход удаляемого воздуха L—10 000 м3/ч, материал воздуховода—сталь (К = 0,1 мм), £Вх = 1,5.

Решение. 1. Средняя по длине воздуховода скорость

0,5-10 000

0,8-0,8-3600

Эквивалентный по скорости диаметр

2-0,8-0,8

D __-------------------------------------------------- = 0,8 м.

0 0,8 + 0,8

2,2-0,8

110 000.

15,6. Ю-6

Коэффициент сопротивления трения по формуле А Д. Альтшуля:

68

0,1 0,25 + — = 0,018. 110 000 800/

2. Ширина щели определяется по формуле (XI.112) с занесением результатов расчета в табл. XI.8.

Таблица XI.8

10 000

— 3,7 м/с.

3600-5-0,151 4. Полное давление (разрежение) в сечении х = 1: 1,5-3,72-1,2 4,342-1,2

12,2 — 11,3 = 0,9 Па.

Расчет воздуховодов равномерного всасывания при постоянных скоростях и расходах в щели постоянной ширины (см. рис. XI.20, а, б) сводится к обычному аэродинамическому расчету разветвленных си­стем. Специфика заключается в том, что целью расчета является подбор длины и шага рассечек, устанавливамых в этих воздуховодах. Для расчета таких воздуховодов имеются инженерные способы, приведен­ные в справочных пособиях [44].