ОТОПЛЕНИЕ И ВЕНТИЛЯЦИЯ

ТЕПЛО — И ВЛАГООБМЕН В АППАРАТАХ КОНДИЦИОНИРОВАНИЯ ВОЗДУХА

Распространенными аппаратами для тепловлажностной обработки воздуха в установках кондиционирования являются форсуночные каме­ры, орошаемые насадки и другие устройства, позволяющие осущест­влять изменения его параметров в широком диапазоне. В теплый пе­риод года можно охлаждать и осушать воздух, охлаждать его при неиз менном влагосодержании, охлаждать и увлажнять его. В холодный пе­риод года используют адиабатическое увлажнение, а также контактный нагрев воздуха.

Постановка задачи расчета тепло - и влагообмена в аппаратах кон­диционирования воздуха встречает значительные трудности, что застав­ляет вводить в описание картины процесса упрощающие предпосылки и часто ограничиваться только экспериментальными данными. Экспери­ментальные характеристики получены для различных аппаратов, в ко­торых воздух специально приготовляется путем контакта с нагретой или охлажденной водой. В одних аппаратах вода разбрызгивается и воздух продувается через дождевое пространство с каплями различной дисперсности, в других она может стекать в виде пленок, образуя вспе­ненный слой или гладкую свободную поверхность. Взаимное направле­ние потоков воздуха и воды (рис. VI.1) и продолжительность их кон­такта между собой также могут быть различными.

Рассмотрим общую физическую картину процесса и влияние от­дельных факторов в логической последовательности, обычно принятой в теории тепло - и массообмена. Прежде всего следует определить тер­модинамические потенциалы и силы, а также потоки тепла и влаги, воз­никающие в системе «воздух — вода». Далее необходимо выявить рав­новесные состояния между воздухом и водой при различных их коли­чественных соотношениях и параметрах. Имея эти данные и составив ба­лансовые уравнения для воздуха и воды, а также уравнение обмена, можно рассмотреть динамику нестационарных процессов тепло - и вла­гообмена. При расчетах аппаратов кондиционирования обычно необхо­димо знать промежуточные состояния воздуха и воды в процессе их перехода от произвольного начального состояния к некоторому равно­весному конечному состоянию.

Оценка термодинамических потенциалов, сил и потоков в системе «воздух — вода». Рассмотрим, следуя U. Marmai («Luft-und Kaltete-

Рис. VI.1. Схемы взаимного движения а'________________

Воздуха и воды в камерах орошения Ь

А — параллельный ток; б — противоток; в — перекрестный ток

5—425

Chnik», 1974, № 5), полную систему «воздух — вода», включающую тол­щу воздуха и толщу воды с соответствующими пограничными слоями у поверхности раздела. Уравнения передачи тепла и влаги в соответствии с теорией тепло - и массообмена запишем с учетом взаимного влияния процессов. Для потоков явного «я» и полного «п» тепла q и влаги / от поверхности воды в воздух:

92--------------------------------------------------- 4v'B-e/VPB; (VI. 28)

<£ = <7в+ [3]/в; 1 (VI. 29)

/в = — VPb — Sq =— Ив V®b - (VI. ЗО)

Для потока тепла из воды к ее поверхности

<7ж = — Яж^ж. (VI. 31)

Граничное условие теплообмена на поверхности воды имеет вид

Й = ЯІ + ІІь = Яж. (VI. 32)

Для системы в целом потоки тепла и влаги определяются разностью температур и разностью потенциалов влажности толщ воздуха и воды:

<7в-ж = + Бі д@в-ж; (VI.33)

/в-ж = В* ©в_ж + Bq (VI.34)

В приведенных уравнениях градиенты у поверхности V и разностиД температур t, парциальных давлений водяного пара р и потенциалов влажности ©* обозначены индексами, относящими их соответственно к воздуху (в), воде (ж) или системе «воздух — вода» (в—ж). Эти гра­диенты и разности термодинамических потенциалов (t, р, ©) являются силами, вызывающими соответствующие потоки тепла и влаги. В урав­нениях приняты также следующие обозначения: ?ів и — проводимость тепла соответственно в воздухе и воде; 8} и 8q — показатель соответ­ственно влаготепло - и тепловлагопроводности; DB — проводимость диф­фузии водяного пара в воздухе; кв— проводимость влаги в воздухе; /Си В — коэффициент передачи соответственно тепла и влаги; Бд и Бч — показатель соответственно влаготепло - и тепловлагопередачи. Показа­тели тепловлаго - и влагогепло-проводности и передачи учитывают вза­имное влияние явлений тепло - и влагообмена.

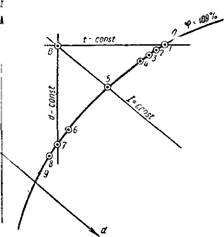
Анализ полной системы уравнений (VI.28) — (VI.34) показывает, что характерных критических точек в процессе тепло - и влагообмена воз­духа с водой не три, как это следовало из простейших представлений (см. § 15), а восемь (рис. VI.2). Эти точки соответствуют следующим состояниям:

1 — градиент температуры в воздухе у поверхности воды V/B = 0;

2 — поток явного тепла в воздухе qkl~6;

3 — разность температур воздуха и воды Д^в_ж=0;

4 — поток тепла от воздуха к воде дв~ж = 0;

5 — поток тепла и градиент температуры в воде у ее поверхности qm = 0, Vf* = 0;

6 — поток влаги и градиент потенциала влажности в воздухе у по­верхности воды /в=0, V©B=0, а также поток влаги /в-ж=0;

7 — градиент парциального давления водяного пара в воздухе у поверхности воды VpB=0;

8 — разность потенциалов влажности воздуха и воды Д©в-Ж = 0.

Точки 0 и 9 на рис. VI.2 и VI.3 не относятся к характерным крити­ческим точкам.

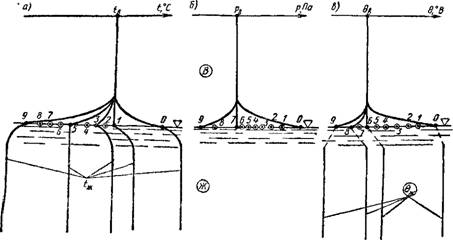
На рис. VI.3 показаны кривые распределения температуры, парци­
ального давления и потенциала влажности, соответствующие этим критическим точкам.

Из общей постановки задачи те­пло - и влагообмена в системе «воз­дух — вода» следует, что для полу­чения количественных результатов нужны данные о проводимости и пе­редаче тепла и влаги, а также о по­тенциале влажности влажного воз­духа.

Число Льюиса и уравнение Меркеля. Следующей важной зада­чей является выявление соотноше­ния интенсивностей тепло - и влаго­обмена, которое определяется чис­лом Льюиса. С ним связано уравне­ние Меркеля, используемое для ра­счета передачи полного (явного и скрытого) тепла. По поводу право­мерности применения этих зависи­мостей имеются довольно противоречивые мнения.

Для нахождения соотношения интенсивностей тепло - и влагообме­на (числа Льюиса) удобно воспользоваться аналогией Рейнольдса, предложенной для отыскания подобия между теплообменом и трением в турбулентном потоке жидкости.

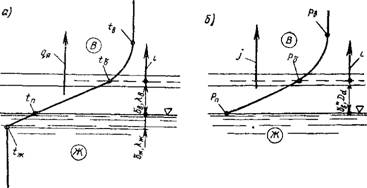
На рис. VI.4 показаны две трактовки обменных процессов. Первая из них основана на законе Ньютона, согласно которому
точно, но не изменяет существа дела, так как в обычном для кондицио­нирования воздуха диапазоне параметров [tm 20° С, В ж 106 Па, см. формулу (III. И)] Д(і^0,84Др, и поэтому pd~l,2pp.

Вторая трактовка основана на аналогии Рейнольдса, согласно кото­рой обмен происходит в результате молярного переноса масс влажного воздуха. Масса влажного воздуха і, перенесенная из пограничного слоя,

5)

Trh=L

/3d-

Рис VI.4. Тепло - и влагообмен воздуха с водой

А — при использовании закона Ньютона; б — при использовании аналогии Рейнольдса; і — погра­ничный слой воздуха; 2 — толща воздуха

В силу сплошности и неразрывности среды компенсируется такой же массой і, переносимой из ядра потока в пограничный слой. Тогда при теплоемкости влажного воздуха с

Приравнивая правые части соответствующих уравнений (VI.35) — (VI.38), получим

A = fc; (VI. 39)

Р d=t. (VI.40)

Из последней записи ясно, что

Как обычно и записывают соотношение Льюиса. Отсюда можно сделать следующий важный вывод: в случае, есш обменные процессы полно­стью определяются молярным переносом масс влажного воздуха, то со­отношение (число) Льюиса будет, безусловно, справедливо незавйсимо от термо - и гидродинамических условий процесса.

Распространяя принятое сопоставление на обмен полным теплом, получим, с одной стороны,

Яп = a (h - /2) + фа {d1 - d2);

С другой стороны,

Яп=і(Іі-І2).

Учитывая, что по формуле (VI.40) i—|3d, запишем зависимость

Яп = (h~h),

Которая является уравнением Меркеля. Следовательно, сделанный ра­нее вывод об условиях применимости соотношения Льюиса полностью распространяется и на уравнение Меркеля.

Из выполненного анализа также следует, что в условиях, соответ­
ствующих применимости аналогии Рейнольдса, все формы тепло - и вла­гообмена могут быть определены одним коэффициентом переноса

Q« = $db(ct); (VI.45)

/ = (VI. 46)

?скр = М(М); (VI. 47)

<7п=М/. (VI. 48)

При некоторых соотношениях параметров воздуха «1» и воды «2» могут возникнуть условия, когда поток явного тепла от воздуха к воде будет противоположен потоку влаги и скрытого тепла от воды к возду­ху. Тогда

Яп ~~ Яя <?скр = Pd {ctt — с/а) — ft* (Idi — Idj) = [(c^ + Idj) — (ct2 + ld2)] =

(VI.49)

Т. e уравнение Меркеля и в этом случае качественно соблюдается.

Но так обстоит дело, подчеркнем еще раз, только если передача тепла и влаги определяется молярным переносом и молекулярным об­меном можно пренебречь. В действительности молекулярный перенос над плоской поверхностью воды, над поверхностью капель может играть заметную роль в общем обмене.

Чтобы дать количественную оценку совместного молярного и мо­лекулярного переноса, воспользуемся предложением Прандтля, который развил аналогию Рейнольдса введением эффектов молекулярного пере­носа в пограничных слоях.

В воздухе и воде у поверхности раздела — поверхности испарения — формируются пограничные слои. В воздухе пограничные эффекты про­являются сильнее, в воде они выражены менее рельефно. Картина теп­ло - и влагопереноса оказывается такой: по мере удаления от поверхно­сти раздела наблюдается постепенный переход от молекулярного к мо­лярному турбулентному обмену.

В противовес рассмотренному чисто молярному переносу разберем второй крайний случай, когда процесс обмена полностью определяется только молекулярным переносом. Такое положение возможно при ма­лой скорости движений сред относительно друг друга и небольшой ин­тенсивности обмена в условиях параллельно-струйного течения вдоль поверхности (поток Куэтта). В этих условиях обмен определяется мо­лекулярной проводимостью тепла и влаги в пределах пограничных сло­ев, и его уравнения можно записать в двух видах:

<?я = « (*в Ив - *жУ, (VI. 50)

°t

/ = РР (Рв - Рж) = ~- (Рв - Рж). (VI. 51)

Следовательно, соотношение интенсивности тепло - и влагообмена (число Льюиса) в этом втором крайнем случае будет равно:

Сс сс Яв б

Т = = Т7Г • <VI-52)

Рр 0,84 Pd О tDB

Если предположить, как это часто делают, равенство толщин теп­лового бt и гидродинамического б пограничных слоев, то искомое соот­ношение будет пропорционально отношению теплопроводности возду­ха Хв и диффузии водяного пара в воздухе DB:

А %в

^=0,84 —. (V1.5D

Следовательно, число Льюиса — отношение коэффициентов тепло - и влагообмена — в общем случае молярно-молекулярного переноса мо­жет находиться в пределах, определяемых соотношениями (VI.41) и (VI.53), т. е

Ос. Яв

При температуре влажного воздуха около 0° С подстановка соответ­ствующих числовых значений в соотношение (VI.54) дает1

0,284 (0,245) >—>0,271 (0,234). Р d

Чтобы установить физическую природу перехода от одного предель­ного значения к другому, рассмотрим схему обменных процессов с уче-

Том пограничного слоя (рис. VI.5). Примем, что в пределах погранич­ного слоя воздуха толщиной бв (до температуры t6) происходит только молекулярный перенос тепла, а от границы этого слоя — только моляр­ный перенос. Тогда

= (v1-66)

Ив

Или

1

— = а((п — tB).

Бв, I

----------------------------------------------- 1----

Ав їс

Если учесть, кроме того, долю | явного тепла (в общем потоке пол­ного тепла), преодолевающую сопротивление пограничного слоя воды толщиной бж:

Рассуждая аналогичным образом применительно к процессу мас - сообмена от поверхности воды через гидродинамический пограничный

Слой в воздух, имеем «

/ =-------------------- —~(dn-dB)=----------- (da-dB)^$d(dn-dB). (VI.60)

5В

-f —- 1 + — і й D*d

Из полученных зависимостей следует, что искомые соотношения ин - тенсивностей тепло - и влагообмена равны:

<5

1 + D 1

---------------------------------------------------------------------- - СТ) (VI .61)

Р d, , Ов

1+ 1С Ав

Или с учетом передачи доли явного тепла через пограничный слой воды

Б:

--СЦ', (VI.62)

Где г] и г]' — поправочные коэффициенты к соотношению (числу) Льюиса (соот­ветственно для а/р<г и К'/fid), учитывающие доли участия молярного и молекулярного переноса в общем процессе тепло - и влагообмена воздуха с водой

Передача полного тепла в рассмотренной схеме равна:

Бж _бв_ _J_ [*ж *R ( К + *с )j Аж Яв 1С

^ж — ^в + ~ jj = /С (г'ж — *услЬ (VI. 63)

ГДе /уел — условная температура воздуха с температурной добавкой, учитываю­щей теплообмен скрытым теплом фазовых превращений воды: /уел —

В рассмотренной расчетной схеме принят ступенчатый переход от молекулярного к молярному переносу. В действительности этот переход будет постепенным, и для получения более точного результата вместо сложения соответствующих сопротивлений в условных пограничных слоях необходимо провести довольно сложное интегрирование, которое здесь не рассматривается.

Равновесное состояние в системе «воздух — вода». При решении задачи о нестационарном обмене в переходном процессе от заданного неравновесного состояния к равновесному установившемуся состоянию необходимо знать, кроме основных уравнений баланса и обмена, гра­ничные временные и пространственные условия и в качестве одного из временных граничных условий конечное равновесное состояние, к ко­торому стремится рассматриваемая система.

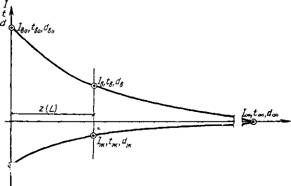
Задача (рис. VI.6) состоит в отыскании предельного равновесного состояния, к которому придут в результате тепло - и влагообмена воздух и вода при заданных начальных количествах и параметрах.

Заданы начальные условия для воздуха: tB0, /во, dB0, его количество GB и начальные условия для воды: /жо, ^жо, ее количество Gm (здесь и далее символами 1 ж и и® обозначены энтальпия и влагосодержание насыщенного водяными парами воздуха непосредственно у поверхности воды с температурой /«).

Требуется определить конечные параметры равновесного состояния too, I ОО, d<X>. которые будут общими и для воздуха и для воды. Величи­ны GB и Gjk останутся практически неизменными, так как предполага­ется, что Gm>GB(doo—dB0).

Запишем уравнение баланса полного тепла, согласно закону сохра­нения энергии, в виде

Д(3п = СвО - ■' -) '°в= - 'жо) °жСж (VI .64)

Или, обозначив G® /G В----

И уравнениями связи между параметрами воздуха на линии насыще­ния ф= 100%:

/ = 9,2+ 1,48/+ 0,0485 /а или / = 2,2 + 0,354? + 0,0116/2; (VI.67)

D = 3,8+ 0,25^+0,017^. (VI .68)

Подставляя в балансовое уравнение (VI.65) разность энтальпий по выражению (VI.66) и заменяя d зависимостью (VI.68), после простых преобразований получим:

І во + 4,18 ц /жо —9,65 /во + Міжо —2,3 спч

* ~------------------------------------------------- или tm к,------------------------------- . (VI. 69)

1,79 + 4,18 її + 0,0418 /жо 00 0,43 + ц + 0,01^жо V '

Имея too, величину /оо можно получить или из уравнения (VI.65) в виде

Или по уравнению (VI.67). Также, зная too, по выражению (VI.68) по­лучим doо.

Уравнения обмена и баланса тепла и влаги в системе «воздух — во­да». В аппаратах кондиционирования воздуха происходят переходные процессы тепло - и влагообмена воздуха с водой. Однако из-за ограни­ченности протяженности поверхности обмена или продолжительности Дг контакта воздуха с водой на выходе из аппаратов они не успевают до­стигнуть своего равновесного состояния, а имеют некоторые промежу­точные параметры (см. рис. VI.6). В связи с этим возникает необходи­мость в рассмотрении общей задачи нестационарного обмена. Задача может быть прямая, когда для заданного аппарата и режима его рабо­ты надо рассчитать параметры на выходе, или обратная, когда по за­
данным параметрам на выходе необходимо определить режим работы или размеры аппарата. Полная физико-математическая постановка за­дачи для этих случаев будет общей. В аппаратах возможно различное взаимное направление движения воды и воздуха (см. рис. VIЛ), но, на­пример, для оросительных камер с несколькими рядами разнонаправ­ленных форсунок наиболее характерным режимом является хаотическое перемешивание, когда можн< задать только некоторую продолжитель­ность контакта воздуха с водой.

Имеется множество предложений по написанию основных диффе­ренциальных уравнений процесса. Отличие в основном состоит в выбо­ре поверхности или объема, определяющих обмен. Поскольку в реаль­ных аппаратах площадь фактических поверхностей обмена установить чрезвычайно трудно, представляется целесообразным для рассмотрения полной постановки задачи пользоваться общими показателями тепло­передачи К и влагообмена Ва для аппарата в данном режиме его ра­боты.

Если принять для упрощения, что при хаотическом перемешивании и больших скоростях сред определяющим является молярный перенос, и, следовательно, справедливо уравнение Меркеля, то уравнение пол­ного теплообмена можно записать в виде

DQn — Bd (/в —(VI. 71) а уравнение явного теплообмена — в виде

DQa = K(tB — tyK)dz. (VI. 72)

Приращения энтальпии и температуры потока воздуха равны:

DQn

Dlв = (VI. 73)

Gti

DQn

= (VI. 74)

T'в св

Приращение температуры потока воды равно:

Dt-M. . (VI.75)

^ж сж

Последнее уравнение можно преобразовать, имея в виду возмож­ность получения производной dtnJdla из соотношения между энтальпией и температурой воздуха на линии насыщения (VI.67):

DQn

D/x=--------------------------------------------------------- ТЗГТ - (VI-76)

Dh

Используя рассмотренные соотношения, можно записать общие дифференциальные уравнения нестационарного тепло - и влагообмена воздуха с водой в аппарате в следующем виде:

Для воздуха по полному теплу

GBdIB = Bd(IB-IyK)dz; (VI. 77)

Для воздуха по явному теплу

" GB св dtB = К (гв - *ж) dz; (VI.78)

Для воды по теплу

Ож СЖ dIM = Bd (/ж - /в) dz - (VI.79)

Шж

Для воздуха по влаге

IBddB = Bd(dB-dx)d2. (VI. 80)

Обычно дифференциальное уравнение для тешюобменных аппара­тов записывают относительно разности'параметров обменивающих сред. Для нашего случая, пользуясь уравнениями (VI.77) и (VI.79), получим

/ 1 а!/ж/Йж d (/в - /ж) - — + г dQn =- mdQn. (VI. 81)

"ж Сж /

Из уравнения (VI.67) имеем

TOC o "1-3" h z dl Ж dl А!

1,48 +0,0485 илк -—^- = 0,354 + 0,0116ґж, (VI.82)

DUк dt_

Поэтому т здесь можно представить в виде

1 , 1,48 + 0,0485 tm 1 0,354 + 0,0116**

-т = — +------------------------------------------- или — т— — Ч—-------------------------- (VI.83)

"в ^Ж СЖ 'JB ^Ж Сж

С учетом уравнения (VI.71) дифференциальное уравнение для раз­ности энтальпий имеет вид

DUs — Іж)

—~~=—mBddz. (VI. 84)

'в —'ж,

Решение уравнения вида (VI.84) известно из курса «Строительной теплофизики». Оно имеет вид

„ / в — I ж —тВЛг

= "Г---------------------------------------------------- Г~ = е • (VI.85)

'во 'жо

.Из него, в частности, следует, что средняя разность энтальпий воз­духа и воды Д/=/в—/ж в этом процессе определится как среднелога - рифмическая разность, т. е. в виде

— Д/0 — Д/

. (VI.86)

Где Д/о=/во-~^жо; А/ = /в-—/ж в конце процесса обмена.

В выражении (VI.85) принято, что т и Bd постоянны, хотя в дей­ствительности они изменяются в процессе обмена. Учет этого обстоя­тельства осложнит решение, но его логическая последовательность оста­нется неизменной.

Решение (VI.85), написанное для разности энтальпий, не позволя­ет, однако, получить параметры воздуха на выходе из аппарата (прямая задача), что часто должно быть основным результатом расчета. Ответ на этот вопрос можно получить, решая уравнения (VI.77), (VI.78), (VI.80) и определяя параметры равновесного состояния рассматривае­мой системы «воздух — вода» по уравнениям (VI.69) и (VI.70). В об­щем виде решение имеет вид, известный из курса «Строительной тепло­физики»:

E=e-Fo. (VI. 87)

В уравнении (VI.87) в является относительным избыточным значе­нием искомого параметра, например температуры воздуха

®tB~ 1Ъ~[°° . (VI.88)

Ь0

Показатель степени в уравнении (VI.87) есть критерий Фурье, опре­деляемый относительно соответствующих показателей общей емкости С, общего сопротивления обмену R и его продолжительности ДZ, в виде

Az

Ро=—. (VI.89)

Например, для обмена явным теплом потока воздуха

1 АгК

С ~ GB св; /?= — ; Fo=—— , К GBcB

И решение для определения температуры воздуха на выходе из аппара­та при продолжительности контакта Дz получим в виде

A ZK

EiB= ° ~ GbV (VI.90)

В0

Для расчета обмена полным теплом и влагообмена воздуха с водой С= GB и R= l/Ва; в остальном решение аналогично (VI.90).

Решение (VI.87) справедливо также для определения параметров воды на выходе из аппарата.

Рассмотренная задача, как было сказано, относится к случаю хао­тического перемешивания воды и воздха в течение ограниченного про­межутка времени. Если в аппарате четко определено взаимное направ­ление потоков (например, в пленочных камерах), то решение можно по­лучить в той же последовательности, заменив продолжительность кон­такта соответствующей протяженностью поверхности контакта. В этом случае сопротивления обмену должны быть отнесены к единице протя­женности поверхности контакта. Взаимное направление потоков воды и воздуха (см. рис. VI. 1) может быть учтено поправочными коэффици­ентами, обычно применяемыми при расчете теплообменников.