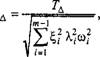Основы ТЕХНОЛОГИИ МАШИНОСТРОЕНИЯ
Расчет плоских размерных цепей
Методика расчета размерных цепей, расчетные формулы зависят от выбранного метода достижения точности замыкающего звена. В связи с этим ниже излагаются методики расчета размерных цепей по каждому из методов достижения замыкающего звена.
Расчет размерных цепей методом полной взаимозаменяемости. При решении прямой задачи, когда требуется установить допуски на составляющие звенья, исходя из допуска замыкающего звена, должно соблюдаться условие:
|
M-1
|
Сначала назначают допуски на составляющие звенья одним из способов, изложенных в п. 1.3.2.1. Наиболее часто вначале определяют средний допуск
Принимая его за допуск составляющего звена.
Затем для каждого составляющего звена осуществляется корректировка допуска со значением коэффициента сложности его достижения.
Далее проводится проверка правильности назначения допусков путем решения уравнения (1.3.3). Если получится неравенство, то в допуски на составляющие звенья вносят соответствующие коррективы.
Затем определяют координаты середин полей допусков на составляющие звенья, за исключением одного. Решая уравнение (1.3.5) с одним неизвестным, находят координату его середины поля допуска.
При расчете полей допусков и координат их середин часты случаи, когда приходится учитывать ограничения, установленные стандартами и другими нормативными материалами; обязательность их учета не затрагивает существа расчетов и их методической направленности.
Правильность рассчитанных допусков может быть проверена путем определения по установленным значениям полей допусков составляющих звеньев и координат их середин предельных отклонений замыкающего звена и сопоставления их с условиями задачи.
Предельные отклонения замыкающего звена могут быть найдены по следующим формулам:
TOC \o "1-3" \h \z m-1 m-1
І=і (=і
M-1 m-1
1=1 ы
где Днд - нижнее предельное отклонение замыкающего звена; ДвД - верхнее предельное отклонение замыкающего звена.
. Рассмотрим пример обеспечения требуемой точности замыкающего звена методом полной взаимозаменяемости.
Задача. Обеспечить зазор между торцами зубчатого колеса и про - ставочного кольца в механизме (рис. 1.3.11) в пределах 0...0,2 мм.
Замыкающим звеном АЛ является размер, связывающий торцы зубчатого колеса и проставочного кольца; уравнение размерной цепи имеет вид
ЛА = - Л1 + Л2-Л3.
Из условий задачи следует, что поле допуска замыкающего звена ТАй =Дмд-Д„лд = 0,2-0 = 0,2 мм, а координата середины поля допуска замыкающего звена
Долд = 0,5(Дмд + )=0,5 (0,2 + 0) = +0,1 мм.
Поскольку размерная цепь является линейной j^. | = 1, то и при
Назначении допусков на составляющие звенья необходимо соблюдение условия
M-1
2 ТА, = ТА д * i=l
При назначении допусков на составляющие звенья надо учитывать степень сложности достижения их точности в процессе изготовления.
Из трех составляющих звеньев наиболее сложно достигается точность звена А2, так как этот размер является наибольшим по величине, кроме того, доступ к нему затруднен и поэтому обработка поверхностей производится консольным инструментом.
Легче обеспечить точность размеров А, и А3; из них проще достигается точность размера А3. Учитывая изложенное, примем
ТАх = 0,03 мм, ТАг = 0,15 мм, TAj = 0,02 мм
И координаты середин полей допусков
Д0/)і =-0,015 мм, Аоа = 0,075 мм.
Координату середины поля допуска третьего звена находим из урав-
Т-1
Нения Л0Ал = ^a. Aqa. =-A<m, + аоа2 - дсмз. где неизвестным являет - 1=1
Ся A0Aj ; тогда 0,1 = 0,015 + 0,075 - А0Л} .
Решая последнее уравнение относительно Аоа, получим А0Лз =
= -0,01 мм. Правильность назначения допусков проверяется через определение предельных отклонений замыкающего звена:
M-1 m-1
/-і (=1 = (0,015 + 0,075 + 0,01) - 0,5 (0,03 + 0,15 + 0,02) = 0;
M-1 m-1
Двл = Х^Аа - +Z = /=1 і=І
= (0,015 + 0,075 + 0,01) + 0,5 (0,03 + 0,15 + 0,02) = 0,2 мм.
Сопоставление с условиями задачи показывает, что допуски установлены правильно.
Расчет размерных цепей методом неполной взаимозаменяемости.
При расчете допусков по методу неполной взаимозаменяемости используют уравнение (1.3.10) на с. 56.
Исходным для решения прямой задачи является величина допуска замыкающего звена и допустимая доля риска Р (в %) выхода замыкающего звена в партии изделий за пределы поля допуска.
Выбор величины Р обосновывается технико-экономическим расчетом. Например, для партии изделий необходимо учесть затраты на изготовление деталей и сборку изделий в количестве, соответствующем доле Р, и сопоставить с общей выгодой, которую дает расширение допусков на составляющие звенья при изготовлении деталей и сборке изделий.
Расчет начинается с установления среднего допуска на составляющие звенья с помощью уравнения
|
|
|
Т |
(1.3.13)
Зная величины Т, m и Р, определяем коэффициент риска t и коэффициент А,-, характеризующий закон рассеяния отклонений 2-го составляющего звена, после чего определяется значение как среднеарифметическое значение X' всех составляющих звеньев.
Значение коэффициента риска? д выбирают из таблиц значений функции Ф(гд) Лапласа в зависимости от принятого риска Р (в %). При нормальном законе распределения отклонений и равновероятном их выходе за обе границы поля допуска
|
Риск Р, %........... Коэффициент t |
Некоторые значения коэффициента? приведены ниже:
32,00 10,00 4,50 1,00 0,27 0,10 0,01 1,00 1,65 2,00 2,57 3,00 3,29 3,89
Значения Хі устанавливаются с учетом возможных условий, в которых будут протекать технологические процессы.
Наиболее распространенными законами, которым подчинено рассеяние отклонений, являются:
- нормальный закон (закон Гаусса), Я.; = 1/9 ;
- закон Симпсона (закон треугольника), = 1 / 6 ;
- закон равной вероятности, А,^ = 1 / 3.
Наиболее вероятным в условиях массового и крупносерийного производства является нормальный закон рассеяния отклонений составляющих звеньев. В тех случаях, когда трудно предвидеть законы распределения отклонений составляющих звеньев размерной цепи, принимают закон Симпсона или закон равной вероятности. При этом следует иметь в виду, что несоответствие фактических законов распределения, принятых в расчете, может повлечь за собой большую долю выхода отклонения замыкающего звена за пределы установленного допуска.
После определения величины среднего допуска производится его корректировка по каждому составляющему звену размерной цепи с учетом сложности достижения его точности. Затем правильность назначенных допусков на составляющие звенья проверяется по формуле (1.3.10).
Координаты середин полей допусков рассчитывают по формуле (1.3.5) так же, как и при методе полной взаимозаменяемости; эти формулы являются общими для всех пяти методов достижения требуемой точности замыкающего звена.
|
|
|
|
Правильность установленных допусков может быть проверена сопоставлением предельных отклонений замыкающего звена с заданными его значениями:
(1.3.14)
(1.3.15)
Для иллюстрации методики расчета допусков при достижении требуемой точности замыкающего звена методом неполной взаимозаменяемости возьмем ранее рассмотренный пример (см. рис. 1.3.11), полностью сохранив условия задачи.
Итак, Тл = 0,2 мм, Т0Ад = +0,1 мм. Зададим значение коэффициента риска tA& , считая экономически оправданным Р = 1 % . Такой доле риска соответствует tA& = 2,57.
Примем, что распределение отклонений составляющих звеньев будет близким к закону Гаусса, тогда Х2Л. = 1/9 .
Учитывая трудности достижения требуемой точности каждого составляющего звена и используя формулу (1.3.10), примем следующие значения полей допусков:
TAj = 0,1 мм; ТАг = 0,20 мм; ТА} = 0,06 мм. При этих значениях ТА
А, д = ТХ = 2,57^|1(0,12 +0,22 +0,062) = 0,2 мм.
Для двух составляющих звеньев установим следующие значения координат середин полей допусков: Д0і4) = 0, А0Лі = 0,1 мм. Значение Д0Лз
Найдем из уравнения: Д0Лд = Д0^ + Д,^ + Д0^, т. е. 0,1 = 0 + 0,1 -
-Долз •
В результате получим Д0/1з = 0.
Правильность установленных допусков проверяется по формулам (1.3.14) и (1.3.15). Используя их, определяем
|
M-1 |
|
Ч 2 , |
M-1
ЛнЛд " ~(Аа 1 X
(=1
|
= 0,1-0,1 = 0; |
|
= (0 + 0,1-0)-2,57, |
( ОД2 + 0,22 + 0,Об2
|
M-1 |
|
І± v 2 у |
|
І=1 |
M-1
ЛвИд - Z^A/li + tA&J X Й,.
1=1
|
0,1 + 0,2 + 0,06 |
|
= 0,1 + 0,1 = 0,2. |
J ((\ i2 , л т2 , л пс2
= (0 + 0,1 - 0) + 2,57 J—
Представляют интерес для выбора одного из двух методов достижения точности данные, приведенные в табл. 1.3.1 и 1.3.2.
|
Таблица 1.3.1
|
|
* Риск Р = 1 %. |
|
Таблица 1.3.2
|
В табл. 1.3.1 приведено сопоставление степени увеличения допусков, рассчитанных методом полной взаимозаменяемости, по сравнению с методом неполной взаимозаменяемости. В табл. 1.3.2 показано увеличение среднего значения допускав? в зависимости от .
Рассмотренные данные иллюстрируют основное преимущество метода неполной взаимозаменяемости - возможность установления значительно больших допусков на составляющие звенья размерной цепи по сравнению с допусками при использовании метода полной взаимозаменяемости, что упрощает и делает более экономичным изготовление деталей.
При использовании метода неполной взаимозаменяемости для одновременного решения нескольких задач у одного и того же изделия или на одном и том же объекте необходимо учитывать, что общий риск может быть больше любого из частных значений риска, принятых при расчете допусков для каждой из размерных цепей.
|
I-na-ft) |
Действительно, если приняты следующие значения риска (в долях единицы): <7і - для первой, q2 - для второй, ..., qs - для s-й размерной цепи, то на основании теоремы об умножении вероятностей общий риск будет
100 [1 - (1 - <?,) (1-92) ... (1 - q,)% = 100
Например, при одновременном использовании метода неполной взаимозаменяемости для достижения точности в трех размерных цепях изделия или объекта общая величина риска
£>з = 100 [(q, + q2 + Яъ) - ІЯі Я і + Я і </з + Яі Яз) + Я і Яг Яъ )%■
При решении обратной задачи, когда известны поля и законы рассеяния составляющих звеньев и координаты их середин полей рассеяния, надо определить возможную величину поля рассеяния замыкающего звена и долю выхода (в %) его значений за пределы установленного допуска у партии изделий.
Расчет возможной величины поля рассеяния замыкающего звена проводится с помощью уравнения (1.3.11).
Расчет Р осуществляется следующим образом: сначала решается уравнение
|
|
|
T |
После по величине гд устанавливается величина Р.
Расчет размерных цепей методом групповой взаимозаменяемости. Расчет начинается с определения Тй9 по методу полной взаимозаменяемости. Величина Гер позволяет оценить уровень точности составляющих звеньев и сопоставить с возможностями производства по его достижению.
На основе этого определяют величину расширения п для получения производственного допуска T'L,
П=пП.
Далее распределяют величину Гд по составляющим звеньям из тех же соображений, что и при расчете методами полной и неполной взаимозаменяемости.
Рассмотрим метод групповой взаимозаменяемости на примере трех - звенной размерной цепи, поскольку любую многозвенную размерную цепь можно привести к трехзвенной размерной цепи.
Чтобы все изделия после групповой сборки правильно выполняли свое служебное назначение, средняя величина зазора или натяга в соединениях каждой группы должна быть одинаковой. Это достигается выпол
нением следующего условия: сумма полей допуско^ увеличивающих звеньев должна быть равна сумме полей допусков ум^ньшающих звеньев, т. е.
Ш-1
/fc+І
Где к - количество увеличивающих звеньев.
Увеличение допусков увеличивающих и умен^шающих звеньев должно осуществляться в таких направлениях, чтобы сохранялась координата середины поля допуска замыкающего звена. У рассматриваемой трехзвенной размерной цепи одно составляющее звено является увеличивающим, а другое - уменьшающим.
|
(=1 |
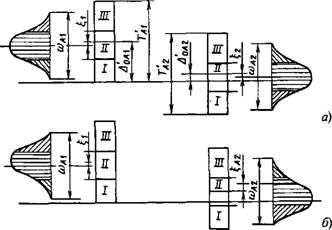
Как следует из рис. 1.3.28, а, замыкающим звеном размерной цепи является зазор, координата середины поля допуска котс>рОГО равна Дод.
|
Аод (Дод, < Д' |
|
Лод, |
Нарис. 1.3.28, б показаны расширенные в 3 раза а разных направлениях поля допусков составляющих звеньев. Из схемы ^ледует, что с увеличением номера группы растет и координата середцны поля допуска
: Д0Дз), а, следовательно, будет раст^ и зазор, который
Должен быть неизменным.
|
S3 |
|
2 чЬЛ. ІЯ, |
|
, 3 И |
|
В) |
|
А) |
|
Г) |
Ff)
Рис. 1.3.28. Схемы расположения полей допуска при использовании метода групповой взаимозаменяемости:
А - заданное расположение; б - при расширенных допу^ках в рщных
Направлениях; в - при расширенных допусках в одном направлении -» <-
В условиях Y. T фЪТ \ г - при расширенных Д0ЦуСках в одном направлении в условиях ЪТ = LT*
На рис. 1.3.28, в показана схема с одинаковым направлением расширения полей допусков составляющих звеньев. Но и в этом случае с повышением номера группы растет величина Дод (хотя и в меньшей степени), так как не выполнено условие равенства допусков увеличивающих и уменьшающих звеньев.
На рис. 1.3.28, г приведена схема расположения полей допусков групп, где выполнены оба условия. В результате с увеличением номера группы координата середины поля допуска замыкающего звена остается постоянной.
При использовании метода групповой взаимозаменяемости следует помнить о дополнительных расходах на измерение, сортировку, клеймение и хранение деталей. С ростом числа групп эти расходы возрастают, поэтому при применении метода групповой взаимозаменяемости надо стремиться к тому, чтобы число групп было по возможности наименьшим.
Следует иметь в виду и то обстоятельство, что допуски на отклонения геометрической формы и поворота поверхностей в группах должны соответствовать не производственному допуску Гд, а заданному допуску 7д. Если это условие не будет соблюдено, то у изделий замыкающее звено может выйти за пределы заданного допуска.
Объясняется это тем, что сортировка деталей на группы производится только по размеру. Поэтому, если допустить, что отклонения формы и поворота составляют 50 % от погрешности размера, то при расширении допуска последнего, например в 3 раза, возрастут примерно в 3 раза и погрешности формы и поворота. В итоге погрешность формы и поворота превысит допуск на размер в группе.
Пример расчета зазора Ад (рис. 1.3.11) методом групповой взаимозаменяемости. Условия задачи: ТА = 0,2 мм; Д0А = +0,1 мм;
/4д = - А] + А2 - А3.
Установим производственный допуск замыкающего звена и число групп, на которые должны быть рассортированы детали после изготовления. Допустим, что расширение допуска ТАл в 3 раза в данном случае
Является экономически обоснованным, в связи с чем число групп примем п = 3. Таким образом, Т'А = 3 ТА = 3 • 0,2 = 0,6 мм.
При расчете полей допусков должно быть соблюдено условие
К m-1
I=l к+1
Согласно этому условию
Т'л2-гАх+гАі = 0,5
Отсюда Т'Аг = 0,5 Т'Ад = 0,3 мм и Т\ + = 0,5 ТА& = 0,3 мм.
Сообразно степени сложности изготовления деталей зададим ТА[ = 0,24 мм и Т'Аъ = 0,06 мм.
Установим значения полей допусков и координат их середин для деталей каждой группы (табл. 1.3.3). При расчете координат середин полей допусков первой группы было использовано уравнение для ҐА.
А0ал = "асм, +а0а2 - а0а2 ■
Координаты сердины полей допусков каждой следующей группы получены путем увеличения координат предшествующей группы на соответствующие поля допусков. Две последние колонки таблицы (Т'аа и
Д0/)д) показывают, что при соединении деталей в каждой группе точность замыкающего звена будет отвечать условиям задачи.
Предельные отклонения составляющих звеньев приведены в табл. 1.3.4.
|
Группа |
7" |
П2 |
Аоа2 |
ДоЛз |
Лсмд |
|||
|
I |
0,08 |
-0,04 |
0,1 |
+0,05 |
0,02 |
-0,01 |
0,2 |
+0,1 |
|
II |
0,08 |
+0,04 |
0,1 |
+0,15 |
0,02 |
+0,01 |
0,2 |
+0,1 |
|
III |
0,08 |
+0,12 |
0,1 |
+0,25 |
0,02 |
+0,03 |
0,2 |
+0,1 |
|
Таблица 1.3.4
|
|
Рис. 1.3.29. Влияние формы и расположения кривых рассеяния на собираемость изделий: А - при одинаковых кривых рассеяния и равенстве величины и знаков смещения середин полей рассеяния; б - при разных кривых рассеяния и неравенстве величины и знаков смещения координат середин полей рассеяния |
Одним их существенных условий экономичного использования метода групповой взаимозаменяемости является соблюдение у составляющих звеньев идентичности законов рассеяния и равенства величины и знаков смещения середин полей рассеяния относительно середин полей допусков. Только при соблюдении этих условий будет обеспечиваться комплектность изделий (рис. 1.3.29, а), не будет избытка одних и нехватки других деталей в группах, т. е. как в случае, показанном нарис. 1.3.29, б.
Расчет размерных цепей методом пригонки. При достижении точности замыкающего звена методом пригонки вначале на все составляющие звенья размерной цепи устанавливаются экономичные для данных производственных условий допуски Т{, Т{ ... Т'т_х. Затем рассчитывается величина компенсации 6К
5К= 7д - Гд,
Которая должна быть удалена с компенсирующего звена.
Далее должны быть назначены координаты середин полей допусков составляющих звеньев.
Произвольное назначение координат середин полей допусков составляющих звеньев может привести к тому, что у компенсатора не окажется нужного запаса материала для пригонки. Для того чтобы обеспечить на компенсаторе минимально необходимый слой материала (припуск) для пригонки, и в то же время достаточный для устранения максимального отклонения замыкающего звена, в координату середины поля допуска компенсирующего звена необходимо ввести поправку Дк.
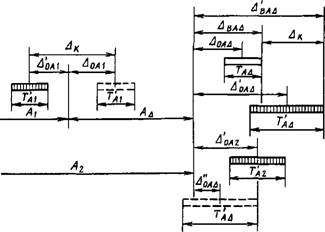
Пусть в трехзвенной размерной цепи А (рис. 1.3.30) требуемая точность замыкающего звена характеризуется величинами и Аоа& ; ТА]
И Т'г - поля допусков составляющих звеньев, экономически целесообразные для данных производственных условий; А'0Л) и A'0Al - координаты середин полей расширенных допусков.
При этих допусках отклонения замыкающего звена Ад возможны в пределах Т'А^ при координате середины полей допуска А'ол& . Наибольшее возможное отклонение Аа отстоит от верхней границы ТАа на величину Дк, значение которой может быть определено следующим путем:
|
Рис. 1.3.30. Схема определения направления Ак |
А(Мд +0,5 Т'Аь =А0Аа +0,5 ТА& + ЛК;
Отсюда Дк = 0,5 6К + - Аоа& .
Если в качестве компенсирующего выбрать уменьшающее составляющее звено А\, то для обеспечения необходимого припуска на пригонку надо в координату Л0А ввести поправку Дк, придав ТА] положение,
Показанное на рисунке штриховыми линиями и характеризуемое координатой AqAt. Новое значение координаты A'0Ai изменит положение Т'л,
Приведет к совмещению его верхней границы с верхней границей и
Обеспечит минимальный припуск на пригонку.
Обобщая рассмотренный случай и распространяя выводы на размерные цепи с любым числом составляющих звеньев, можно записать:
M-1
Дк = 0,55к+&Д'о,-Д0д.
1=1
Отметим, что для устранения недостатка или излишка припуска на компенсирующем звене, если оно уменьшающее, поправку Дк вносят в координату середины его поля допуска со своим знаком. Если компенсирующим является увеличивающее звено, то поправку Дк вносят в координату середины его поля допуска со знаком, обратным полученному при вычислении.
Пример расчета зазора Ал (рис. 1.3.11) методом пригонки. Примем в качестве компенсирующего звена толщину А3 проставочного кольца.
Установим на составляющие звенья экономически целесообразные поля допусков и зададим координаты, мм, середин полей допусков:
|
|
Звено............................................................................. - А і Аг -А3
0,3 0,4 0,1 -0,15 +0,20 +0,25
При этих значениях Т'А. допуск замыкающего звена будет равен
M-1
= XТ'А. = 0,3 + 0,4 + 0,1 = 0,8 мм.
I=i
8к=^4 ~ТАл =0,8-0,2 = 0,6 мм.
Для того чтобы компенсатор имел необходимую для пригонки толщину, в координату середины поля допуска звена А3 следует ввести по-
Правку
M-l
Дк=0,56к + Х^, А'см, ~аоал = 0,5 ■ 0,6 + (0,15 +• 0,2-0,25)-0,1 =0,3 мм.
(=1
Поскольку компенсирующим является уменьшающее составляющее звено, то поправка Дк должна быть введена в координату середины его поля допуска со своим знаком. Отсюда
TqA = 0,25 + 0,3 = 0,55 мм.
Расчет размерных цепей методом регулировки. Принципиально метод аналогичен методу пригонки, различие заключается лишь в способе изменения размера компенсирующего звена.
|
Z
|
|
|
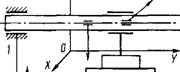
В отличие от метода пригонки методом регулировки достаточно просто можно решать задачи придания требуемого углового положения детали в машине. На рис. 1.3.31 приведена конструкция, позволяющая обеспечивать методом регулировки параллельность оси вала в горизонтальной и в одной из вертикальных координатных плоскостей. Вал устанавливают в средней опоре, а затем на его концах монтируют крайние опоры. Имея возможность перемещаться в направлении осей X и Z, крайние опоры 1 и 2 выполняют роль подвижных компенсаторов. Перемещая их, добиваются требуемой параллельности оси вала в
М///,
З-
|
|
Рис. 1.3.31. Схема достижения параллельности оси вала основанию с помощью подвижных компенсаторов:
|
Наибольшая возможная компенсация |
/ и 2 - опоры
Плоскостях ХО Y и YOZ, а затем положение опор фиксируется крепежными винтами и контрольными штифтами.
Допуски при методе регулирования назначают так же, как при методе пригонки: устанавливают экономически приемлемые для данных производственных условий поля допусков 7j', 'Г',, ..., Т'т_] и координаты
Л;л, До2, ..., До„-1 их середин.
При применении подвижного компенсатора определяют 5К, которую учитывают при разработке конструкции подвижного компенсатора и определении его размера.
При применении неподвижного компенсатора приходится считаться с тем, что неподвижный компенсатор не в состоянии скомпенсировать собственное отклонение. Поэтому в проводимых расчетах допуск, ограничивающий отклонения компенсирующего звена, учитывать нельзя:
|
|
|
Т-2 |
|
Т-2 |
Где т-2 означает, что при суммировании значения 7"к' и компенсатора не учтены. Следовательно,
Далее необходимо определить число ступеней компенсаторов и их размеры. Число ступеней компенсаторов
/V = Гд /(Гд - Гк'),
Где Т^ - поле допуска, ограничивающее отклонения размера компенсатора.
Дія пояснения подхода к определению размеров компенсаторов каждой ступени воспользуемся задачей, рассмотренной ранее (см. рис. 1.3.11).
В качестве неподвижного компенсатора выступает проставочное кольцо а ТАь и Д0<4д - соответственно поле допуска и координата середины поля допуска замыкающего звена Ал, где ТА = 0,2 мм, =0,1 мм.
Произвольный выбор координат Д^ середин полей допусков (т - 2) составляющих звеньев может привести к расположению допуска Т"
4 - II3N2
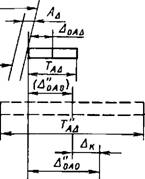
относительно допуска ТА, неудобному для определения размеров компенсаторов (например, к положению, показанному нарис. 1.3.32 штриховыми линиями). Значительно проше определять размеры компенсаторов, имея совмещенные верхние или нижние границы допусков ТА и ТА.
|
|
АА
|
3-я зона |
|
1-я зона |
|
Вязана |
2-я зона
|
Т'лз |
|
'A3 |
|
'a3 |
|
Таз |
Компенсатор ступени!
Jjl
Компенсатор ступени д
А3*0
Компенсатор стдпеШГШ
А3 + 2С
Компенсатор ступени ш
A3 + JC
J___ I___ I___ L
О 0,1 0,2 0,3 0,4 0,5 мм
Рис. 1.3.32. Схема определения размеров ступеней компенсатора
Для совмещения одноименных границ полей допусков необходимо: 1) либо (при установленных значениях Д^ ) ввести поправку А'к в координату середины поля допуска одного из составляющих звеньев, но не компенсирующего звена; 2) либо не устанавливать заранее значения Л'0Аі , а рассчитать их, исходя, например, из условия = Д,^ .
Следуя первым путем и желая совместить нижние границы полей допусков, в координату середины поля допуска одного из составляющих звеньев необходимо внести поправку
Т-2 (=1
Избрав второй путь и соблюдая условие Д^,д = Д1Ыд , будем иметь Отсюда величина An, = Д„ + 0,5 7і! оказывается известной, по-
ЛД а
Скольку значение Дн-4д задано условиями задачи, а значение было
Определено ранее. Далее обычным путем, составив уравнение координат полей допусков, на основании зависимости
К _ т-2_ / = 1 к + 1
Следует установить координаты середин полей допусков (т - 2) составляющих звеньев.
Координату середины поля допуска компенсирующего звена устанавливают независимо от координат других составляющих звеньев. Для упрощения расчета размеров ступеней компенсатора рекомендуется задавать координату середины поля допуска компенсирующего звена, равную половине его поля допуска со знаком минус, т. е. направлять допуск в «тело» компенсатора.
Упорядочив или рассчитав значения координат середин полей допусков и придав ТА удобное положение, можно установить размеры
Ступеней компенсатора.
Размер компенсатора первой ступени равен номинальному размеру компенсатора. Размер компенсаторов каждой следующей ступени будет
Отличаться от размера компенсатора предшествующей ступени на значение С ступени компенсации:
Допуск, ограничивающий отклонения компенсирующего звена, остается одним и тем же для компенсаторов всех ступеней.
На схеме, показанной на рис. 1.3.32, видно, как осуществляется компенсация отклонений, находящихся в четырех зонах ТА, компенсаторами четырех ступеней.
Пример. Зададим поля допусков, считающиеся экономичными в заданных условиях: Т'А = 0,2 мм, Т'А = 0,4 мм, Т'А = 0,05 мм (рис. 1.3.11).
Поскольку в размерной цепи А компенсирующим является звено А3, то компенсации подлежат отклонения звеньев А\ и Л2. В соответствии с этим
Т-2
^=11^-0,2-0,4-0.6-™;
Ы
5К = ГА"Л - ТАа = 0,6 - 0,2 = 0,4 мм.
Число ступеней компенсаторов
N = ТІ /(7д - 7'к') = 0,6/(0,2 - 0,05) = 4.
Рассчитаем координаты середин полей допусков, соблюдая условие
— ДнЛд 1
КА,= ЬІА, -0,5 Т'л.
Отсюда Д^ = ДнЛд + 0,5 ТА& = 0 + 0,5 ■ 0,6 = 0,3 мм.
Таким образом, Д^л = Д[м, = 0,3 мм. Установим Д^ =
= -0,1 мм и Д^, = 0,2 мм.
Независимо
От До,^ и До At координата середины поля допуска компенсирующего звена
\'0А} = - 0,5 ТАъ = 0,5 ■ 0,05 = -0,025 мм.
При ступени компенсации С = ТА - TAj = 0,2 - 0,05 = 0,15 мм поле ТА производственного допуска окажется разделенным на четыре зоны.
Отклонения, возникающие в пределах той или иной зоны, должны компенсироваться путем установки проставочного кольца соответствующей ступени.
Размер компенсаторов первой ступени равен номинальному размеру А3. Размеры компенсаторов каждой следующей ступени будут отличаться от предшествующей на величину С.
С учетом допуска на изготовление размеры компенсаторов будут следующими (в мм):
Ступень / - А-і _0>05;
Ступень II - Из + 0, 15)_о, п5;
Ступень III - (А3 + 0,30)_а 05;
Ступень IV - Из + 0,45)_о, о5;
Разницу в номиналах целесообразно учесть в предельных отконени - ях и установить такие размеры компенсаторов (в мм):
Ступень I - А3 _0 05 ; ступень II - А-, ;
,,, . +0,30 ,,, . +0,45
Ступень III - л, ' ; ступень IV - Л
* +0,25 * +0,40
|
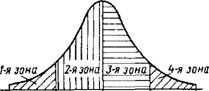
Рис. 1.3.33. Определение числа компенсаторов каждой ступени |
Число неподвижных компенсаторов в каждой ступени делают одинаковым, если нет данных о законе рассеяния отклонений звена в размерной цепи. Если же такие данные есть, то число компенсаторов каждой ступени должно быть пропорциональным соответствующим площадям участков кривой рассеяния, построенной относительно Т"А, как это показано на рис. 1.3.33 для закона нормального распределения.
|
|
|
|