ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ЖЕСТКОСТЬ НАПРЯЖЕННОГО СОСТОЯНИЯ ПРИ ОБОБЩЕННОЙ ПЛОСКОЙ ДЕФОРМАЦИИ
3.1.7.1.
ВЛИЯНИЕ ОТНОШЕНИЙ НАПРЯЖЕНИЙ Графики распределения жесткости напряженного состояния вблизи концентраторов при плоской деформации (sz = 0) были приведены на рис. 3.6, 3.8, 3.11, 3.12, 3.14, 3.16 и 3.20. Из них следует, что на поверхности дефекта жесткость ^ всегда близка к единице. Это объясняется тем, что на поверхности надреза действует
плоское напряженное состояние. По мере углубления в толщу материала жесткость напряженного состояния возрастает. Для внешней двусторонней выточки максимум жесткости ц достигается в центре сечения; для мелких внутренних дефектов и выступов — на расстоянии нескольких радиусов под вершиной надреза.
Чтобы упростить вычисления жесткости напряженного состояния, целесообразно ввести обозначения для соотношений между напряжениями:
Go n G3
а=^' <3.47> Тогда жесткость напряженного состояния можно вычислить как: 1
Л =
д/1 + а2 +Р2 - а-р-ар" (3.48)
При обобщенной плоской деформации, если пластина растягивается в бездефектном сечении напряжениями p0, то:
F =-V-^
Єг0 V E,
и с учетом формулы (3.43):
Ро =v-|^1 + | (3.49)
где индекс 0 поставлен у р, потому что это выражение не учитывает остаточных напряжений.
Если в направлении оси 2 до нагружения конструкции полезной нагрузкой действуют остаточные (например, сварочные) напряжения, то их удобно задать в долях от предела текучести материала:
®zw = m °Т, (3.50)
тогда ^ ^
p=vy+a_l:J+m 'ff=р0+m (3.51)
Последнее равенство написано с учетом того, что при наступлении текучести CTi = Ст.
Если подставить (3.51) в (3.48), то относительно неизвестной ц получится квадратное уравнение вида
A ~ + B • - + C = 0, (3.52)
Л2 Л
где Л 1 2
A = 1 - m2,
B = - m (2 p0 -1 - a),
C = -(1 + a2 +p2 - a-p-ap).
Если A, B и С вычислены, то жесткость напряженного состояния находится по известной формуле для квадратного уравнения:
2 • A
B + VB2 - 4AC • (353)
Но при m = 1 это выражение дает неопределенность, так как квадратное уравнение (3.52) превращается в уравнение первой степени. Поэтому при m = 1 жесткость напряженного состояния следует вычислять по формуле
B =_________ 1 + а - Ро________
C 1 + а2 +Р0-а-р0 - а-р0 . (3.54)
л = -

|
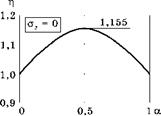
Рис. 3.22 Зависимость ц = oi/ot от соотношения напряжений при плоском напряженном состоянии |
|
= Л |
|
0, |
На свободной поверхности материала одно из главных напряжений всегда равно нулю. Если в формуле (3.54) положить рр = 0, то для плоского напряженного состояния получим
Л=:г-4--------- . (3.55)
1 + а2 - а 4 ’
Эта зависимость построена на рис. 3.22.
Видно, что жесткость напряженного состояния достигает мак симума (г| = 1,155) при а = а2/а1 = = 0,5. При одноосном растяжении (а = 0), так же как при двуосном растяжении (а = 1), жесткость напряженного состояния равна единице. Таким образом, на свободной поверхности любого концентратора максимальные напряжения не могут превосходить (1-1,155) сопротивления пластической деформации материала.
На рис. 3.23 показана зависимость жесткости напряженного состояния от а при плоской деформации (єг = 0) и различном уровне m — растягивающих остаточных напряжений, перпендикулярных нагрузке. Пунктиром на этом ри-
|
£г = |
0 |
5,00 |
||
|
л |
1=1 |
|||
|
т = |
0,5 , |
|||
|
т = С |
2,56 |
|||
|
= 0 |
||||
|
0,506 |
||||
|
0 0,2 0,4 0,' |
|
а |
|
Рис. 3.23 Зависимость жесткости напряженного состояния от соотношения главных напряжений а при плоской деформации |
сунке показана кривая для плоского напряженного состояния, перенесенная с рис. 3.22.
Видно, что при плоском напряженном состоянии максимальная жесткость получается при as 0,9. Если остаточные напряжения в направлении оси 2 отсутствуют (т = 0), то нормальные напряжения могут в упругой стадии нагружения в 2,566 раз превышать предел текучести материала. Однако эта величина сильно возрастает с увеличением остаточных напряжений. Когда они равны пределу текучести (т = 1), как в случае непровара в поперечном нагрузке сварном шве, то максимальные упругие напряжения теоретически могут в 5 раз превышать предел текучести материала.
Низкоуглеродистая сталь с пределом текучести 25 кг/мм2 в этих условиях может выдерживать без пластической деформации нормальные напряжения в 125 кг/мм2. Это очень опасная ситуация. Скорее всего, эта сталь уже при напряжениях менее 100 кг/ мм2 разрушится подобно стеклу. К счастью, такая высокая жесткость напряженного состояния на практике не реализуется.