ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТРЫВУ ОТ ПРЕДВАРИТЕЛЬНОЙ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
Эту зависимость на каменной соли установили A. Ф. Йоффе, М. В. Кирпичева и М. А. Левицкая в 1924 г. Предшествующая пластическая деформация размельчает структуру материала и уменьшает размер субмикротрещин, вызывающих хрупкое разрушение.
Формулу этой зависимости для стали мы составили из следующих соображений. Если круглый образец с диаметром d0 пластически удлиняется до деформации ep, и его диаметр сокращается до d, то, учитывая постоянство объема при пластической деформации, можно записать:
e(L )=(I J=2in (d
откуда
10 = eXP{-t). (6.102)
Если количество зерен в поперечном сечении образца при пластической деформации остается неизменным, то формула (6.102) останется справедливой и для изменения диаметра зерна в поперечном сечении при пластической деформации. Если ep положительна, то диаметр зерна в поперечном сечении будет уменьшаться, если отрицательна (сжатие), то он будет расти.
Но согласно формуле (6.99) сопротивление отрыву обратно пропорционально корню квадратному от диаметра зерна. Поэтому поправка на изменение сопротивления отрыву по этой причине должна иметь вид
d „I e1
|
^ _ л 4d |
|
(6.103) |
|
AS1( ep) = Ьл |
|
= bs1 ■ exp-±- I - 1 I. |
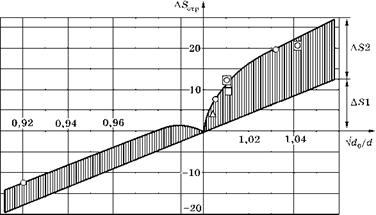
Поправка AS1 представлена прямой наклонной линией на рис. 6.39.
|
Рис. 6.39 Изменение сопротивления отрыва от предварительной пластической деформации круглых образцов |
|
0 |
По оси абсцисс отложено:
= exp
Однако эксперименты показывают, что величина коэффициента bs1 для сталей лежит в интервале 102-280 кГ/мм2. Чтобы сопоставить эти значения с коэффициентом bsd при d-1/2, в формуле
(6.99) были вычислены значения р = bs1 • d0-1/2. Тогда формула
(6.103) примет вид, _
AS1(ef) = _ Ь
4d
и угловой коэффициент р можно сравнивать по величине с угловым коэффициентом bsd формулы (6.99). Этот параметр лежит в интервале 26-90 кГ/мм2, что в 2-8 раз больше, чем коэффициент 11,5 в формуле (6.100). Данный факт говорит о том, что при пластической деформации длина линейных скоплений дислокаций Lp, образующих клиновые субмикротрещины, изменяется в 22-82 раза быстрее, чем диаметр образца. Происходит размельчение структуры.
Экспериментальные результаты показали, что если сталь предварительно деформировать пластически при температурах ниже -100°С, то приращения сопротивления отрыву очень хорошо укладываются на линию, построенную по формуле (6.103). Однако если сталь предварительно деформировать при комнатной температуре, то у сопротивления отрыву появляется еще одна поправка, которая всегда положительна, а скорость ее увеличения затухает с ростом пластической деформации. Мы описали ее формулой
|
|
(6.104)
Экспериментальные результаты, полученные на стали типа Ст3, дали следующие значения постоянных параметров этой фор-
|
|
bs2 = 15,5 кГ/мм2
— если был предварительный наклеп растяжением;
bs2 = 5,5 кг/мм2
— если был предварительный наклеп сжатием.
Эта зависимость выражается формулой
bS2(eip) = if(e1p >0, 15.5, 5.5).
Появление поправки AS2(ep) мы объяснили тем, что если пластическая деформация идет при комнатной температуре, то помимо размельчения структуры (уменьшения длины линейных скоплений Lp) происходит уменьшение неравномерности распределения напряжений второго рода и уменьшение действия других возможных концентраторов напряжений.
В итоге, сопротивление отрыву с учетом пластической деформации можно вычислять по формуле
|
(6.105) |
S,^ (eP) = S^. 0 + AS1(ep) + AS2(ep),
где S^. 0 — сопротивление отрыву, определенное без учета предварительной пластической деформации по формуле (6.99).
Обе поправки показаны на рис. 6.39.