ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ВЛИЯНИЕ КОЛИЧЕСТВА ЦИКЛОВ
Для конструкционных сталей и алюминиевых сплавов к разрушениям при малоцикловой усталости относят обычно такие, которые происходят при числе циклов Nf < 104...105 (индекс f от англ. fracture «разрушение, излом» или failure «разрыв, авария»). Максимальные напряжения в этой области обычно равны или превосходят предел текучести материала, поэтому петлю деформации (рис. 6.67) можно записывать на двухкоординатном самописце по показаниям датчика удлинения рабочей части образца и датчика усилия.
Механизм разрушения в этой области близок к механизму вязкого разрушения при статической нагрузке. Он определяется зарождением, ростом и слиянием пор. Но здесь поры тем мельче, чем больше число циклов Nf до разрушения. Так как раскрытие растущей трещины определяется максимальными нормальными напряжениями стг, усталостные трещины растут почти всегда перпендикулярно траекториям напряжений стг.
Эмпирическая степенная зависимость количества циклов Nf до возникновения трещины от ширины петли Aep при жестком нагружении носит название «зависимости Коффина-Менсона», которая имеет вид:
|
(6.155) |
(Nf )m ■Aep = C,
где m и С — постоянные материала.
Для сталей с пределом прочности ав ниже 70 кг/мм2 показатель степени m очень близок к 0,5. Для более прочных сталей Н. А. Махутов рекомендует вычислять показатель степени m по формуле
где аВ — предел прочности стали, кГ/мм2.
Постоянную С формулы (6.155) можно найти из условия разрушения материала при статической нагрузке. Материал разрушается за Nf = 1/4 цикла, при этом разрушающая пластическая деформация составляет:
|
|
Здесь у — относительное сужение образца при одноосном растяжении.
Подставив количество циклов Nf = 1/4 и деформацию Aep = ef в формулу (6.155), для обычных конструкционных сталей низкой и средней прочности (т = 0,5) получим
4
-) ■ ef = С,
откуда ef і
с=4-=1 • ln
1 - vf
и зависимость Коффина-Менсона для сталей с пределом текучести менее 70 кг/мм2 приобретает вид:
Aep = 2T/Nf • (6Л57)
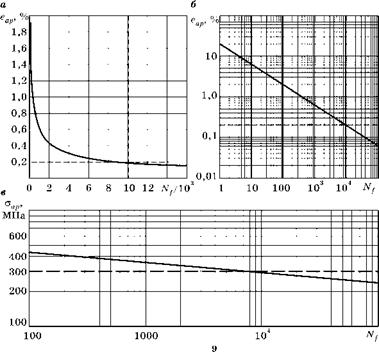
Вид зависимости амплитуды пластической деформации (eap = = Aep/2) от разрушающего числа циклов Nf для стали 22К (ef = 0,749) показан на рис. 6.69a.
|
Рис. 6.6 Зависимость амплитуды пластических деформаций (a, б) и амплитуды напряжений (в) от Nf — числа циклов до разрушения |
На рис. 6.69б та же зависимость построена в логарифмических координатах. Пунктирной прямой показан уровень пластических деформаций при условном пределе текучести (0,2%). Видно, что для этой стали разрушающая деформация становится примерно равной пластической деформации при пределе текучести (0,2%) при 10 000 циклов.
Кроме того, кривая (eap - Nf) в логарифмических координатах становится прямой, которая проще для анализа.
Для пересчета размаха пластических деформаций на амплитуду напряжений можно воспользоваться формулами (6.153) и (6.157), из которых следует
|
|
Эта зависимость построена на рис. 6.69в. Обратите внимание на очень малый наклон линии этого графика. Тангенс угла наклона здесь равен - n/2 = -0,176/2 = -1/11,4 вместо -1/2 у графика рис. 6.69б.
6.4.2.4.
ЛИНЕЙНОЕ СУММИРОВАНИЕ ПОВРЕЖДЕНИЙ
Если нагрузка изменяется во времени, то проще всего при оценке выносливости использовать гипотезу о линейном суммировании повреждений, согласно которой при постоянной нагрузке за каждый цикл в металле возникает одинаковое количество повреждений. Если степень поврежденности материала обозначить буквой d, то в момент разрушения при числе циклов Nf степень повреждения d =1. Nf можно вычислить по формуле (6.157). Тогда приращение повреждений на i-ой ступени нагружения, накопленное за AN; циклов при постоянной Aepi, составит:
|
|
Если ширина петли гистерезиса меняется во времени, то весь интервал изменений Aep разбивают на достаточно большое количество n ступеней нагрузки. По гистограмме нагрузки подсчитывают количество циклов AN; на каждой ступени нагрузки Aepi. Предельное состояние конструкции определяют по условию равенства единице суммы повреждений Adi, вычисленных по фор-
|
|
|
|
В качестве примера рассмотрим спектр нагрузок, приведенный в приложениях к СНиП для сосудов аэродинамических труб, а свойства материала возьмем из табл. 6.8. Исходные значения (из приложения к СНиП) запишем в виде векторов: s = [1; 0,85; 0,70; 0,54; 0,37; 0,28]; 5N = [2, 21, 299, 881, 997, 17 930]. Здесь: i = 0...5 — номер ступени нагружения; sl — уровень давления в сосуде на l-й ступени нагружения, при условии, что pmax = 1 и характеристика цикла r =0; ANl — число циклов, при котором обнаружено sl.
Так как напряжения а пропорциональны давлению p в сосуде, то размах номинальных напряжений Аа1 на l-й ступени нагружения можно вычислить по формуле: Aal = amax • sl. Здесь по условию прочности сосуда при r = 0 размах напряжений должен быть меньше предела текучести: а02 = 291 МПа.
Размах номинальных деформаций для упругой стадии нагружения:
Авн
l E,
где E = 2105 МПа — модуль упругости.
Малоцикловая усталость развивается у концентраторов. Круглое отверстие дает коэффициент концентрации в упругой области (теоретический) kT = 3. У патрубков в сосуде коэффициент концентрации обычно несколько больше. Примем kT = 4. Примем для простоты коэффициент концентрации напряжений йа = 1. Тогда коэффициент концентрации деформаций ks по формуле (3.58) равен:
k2
і. 16.
В результате размах пластических деформаций Aepl в опасной точке сосуда можно вычислить по формуле
|
Aepl — Aef. K—^-. h—^^. ke. (6.160) |
A°l k — ^max. sl
E ' e— E
Полное число циклов, полученное при экспериментальном определении векторов s и 5N, равно сумме всех членов вектора 8N — 20 130. Если в процессе нагружения будет другое суммарное число циклов, равное N, то число циклов на l-й ступени нужно будет вычислять по формуле
. (6.161)
Условие целостности конструкции получим, подставив выражения (6.161) и (6.160) в формулу (6.159):
|
liSN l I { E |
|
• 1 I ef l=1 V f |
|
350 |
|
300 |
|
250 |
|
Рис. 6.70 Зависимость допускаемых напряжений от числа циклов нагрузки |
|
ISN |
|
(6.162) |
|
VN' |
|
■SNi) |
|
Зависимость amax от суммарного Так как формула (6.162) была Очевидно линия amax(N) представ- ния ожидается с вероятностью в 50%. Чтобы из этого результата |
|
E ■ ef ' 2 • k„ |
|
I(s2 i=0 |
|
Это уравнение можно решить относительно amax: |
|
6.4.3. МНОГОЦИКЛОВАЯ УСТАЛОСТЬ 6.4.3.1. МЕХАНИЗМ РАЗРУШЕНИЯ И ВИД ИЗЛОМА Если число циклов нагрузки до разрушения конструкционной стали превышает 104...105, то такие разрушения относят к многоцикловым. Их зарождение (инициация) определяется накоплением дефектов в результате очень локальной знакопеременной пластической деформации. Как правило, напряжения при такой усталости ниже предела текучести. Поэтому суммировать нужно пластические деформации микротекучести в наиболее слабых зернах металла на наиболее слабых полосах скольжения (см. раздел 4.3). Пластические деформации микротекучести нельзя измерить непосредственно, их величину приходится оценивать через напря- |
жения. Поэтому мерой прочности металла при многоцикловой (обычной) усталости является размах напряжений, а не пластических деформаций — как при малоцикловой области разрушений.
Разрушение гладкого образца при обычной усталости проходит три стадии.
На первой стадии оно начинается с разрушения поверхностных зерен. Выше, в разделе 4.3, было показано, что для этих зерен эффективная длина участка дислокации между точками закрепления в два раза больше, чем для внутренних зерен. Поэтому источники дислокаций в этих зернах начинают работать при напряжениях в два раза меньших, чем нужно для внутренних зерен. За много циклов локальной деформации поверхностных зерен в них появляются стабильные полосы сдвига, которые не исчезают при отпуске и глубоком травлении. Это явление связывают с многочисленными микродефектами (порами), образовавшимися в такой полосе скольжения. Как только в зерне появилась стабильная полоса сдвигов, дальнейшая циклическая деформация зерна происходит только по ней.
Этот механизм объясняет существенное упрочнение, которое при циклической нагрузке вызывает нанесение тончайших твердых поверхностных слоев при цементации, напылении и т. п. способах обработки. Такие слои закрепляют свободные концы дислокаций и условия деформации поверхностных зерен становятся близкими к условиям деформации внутренних зерен.
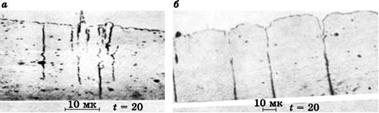
У выхода такой полосы на поверхность происходит микроскопическая «порча» поверхности. На косом шлифе подвергнутой циклической деформации меди (рис. 6.71а) видно, как одни плоскости «выползают» наружу, другие проваливаются внутрь зерна (такую картину может наблюдать каждый, если зажмет между
|
Рис. 6.71 Зарождение усталостного разрушения на поверхности зерна поликристаллической меди (косой шлиф): |
(a) появление выступов и впадин; (б) образование поверхностных трещин на стабильных полосах сдвига.
|
d Рис. 6.72 Разрушение модели патрубка при испытаниях на усталость (фото И. В. Кудрявцева): (а) траектория трещины по c-d; (б) вид поверхности излома. |
ладонями колоду игральных карт и начнет циклически сдвигать ее в одну и другую сторону).
Далее, у выхода стабильных полос сдвига на поверхность возникают поверхностные микротрещинки, видные на рис. 6.71б. По мере роста числа циклов они распространяются вглубь вдоль линий скольжения под углом 45° к поверхности металла и к направлению главных нормальных напряжений.
На первой стадии разрушение распространяется на глубину 12 диаметров зерна от поверхности. На макрошлифе эта зона практически не видна.
Далее наступает вторая стадия, при которой усталостная трещина в микромасштабе продолжает прорастать в направлении главных касательных напряжений под углом 45° к направлению растяжения-сжатия образца, однако часто меняет свое направление на 90°. Поэтому в макромасштабе трещина распространяется перпендикулярно направлению максимальных нормальных напряжений стг. В результате многократного раскрытия и закрытия макротрещины при циклической нагрузке с отрицательной характеристикой цикла r микровыступы, образовавшиеся при смене направления микроразрушения, истираются. Образуется черный металлический порошок, часто видный на поверхности усталостного излома.
Макроструктура такого излома показана на рис. 6.72б. Общий вид разрушения детали у вваренного штуцера показан на рис. 6.72а.
Макроскопически излом на второй стадии образует гладкую поверхность. Направление распространения трещин на рис. 6.72б показано черными стрелками. Видно, что на этом изломе усталостные
трещины распространялись не менее, чем от четырех различных источников.
|
Рис. 6.73 Бороздки на поверхности усталостного излома стали 45. Трещина распространялась снизу вверх. Растровый микроскоп, х10 500 |
При большом увеличении на поверхности усталостного разрушения зерна видны сглаженные при истирании микроскопические бороздки (рис. 6.73).
Вероятно, их появление связано с тем, что накопление повреждений идет по линиям скольжения, ориентированным под углом 45° к поверхности излома. Выход пересекающихся плоскостей с повреждениями на поверхность излома должен оставлять микроскопические бороздки, каждая из которых соответствует продвижению трещины на одном или нескольких циклах нагрузки.
Скорость распространения усталостной трещины возрастает с увеличением ее длины. Это происходит потому, что с длиной трещины возрастает размах коэффициента интенсивности напряжений AKI, определяющего скорость ее роста. Фронт трещины на поверхности излома оставляет макроскопические следы в виде дуг эллипсов, на которые указывают черные стрелки (рис. 6.726). Выпуклость дуг всегда направлена в сторону распространения трещины. Поэтому по этим дугам при анализе причин аварий можно найти дефект, послуживший причиной зарождения рассматриваемой трещины.
С ростом площади усталостных трещин возрастают средние напряжения в неразрушенном сечении. Когда они приближаются к пределу прочности материала, за один полуцикл нагрузки происходит долом оставшегося сечения по механизму вязкого разрушения. На рис. 6.72б на зону долома показывают белые стрелки.
Но иногда усталостное разрушение переходит в хрупкое разрушение. Тогда переход к долому часто описывают в терминах механики трещин критерием: К1 = К1С.
При математическом моделировании процесса усталостного разрушения обычно используют метод конечных элементов. Используя стандартные пакеты программ этого метода, при циклической нагрузке вычисляют приращения пластических деформаций при каждом цикле нагружения с учетом влияния концентрации напряжений и остаточных напряжений и повреждений материала в виде пор, возникающих на полосах скольжения.
Процесс моделирования разбивают на два периода. В первом вычисляется образование и рост малых трещин. Такие трещины некорректны в терминах механики разрушения. Поэтому накопление дефектов и рост малых трещин определяется накоплением средней по наиболее нагруженному зерну металла интенсивности деформации: Ає; = єг, max - єг, min. Вычисление похоже на вычисления при определении условий вязкого разрушения, но отличается от него тем, что процесс роста пор нарастает при каждом полуцик - ле нагружения.
Во втором периоде, когда длина трещин l превышает 2-3 мм, линейная механика разрушения обычно становится корректной. На этой стадии скорость роста трещины определяется размахом коэффициента интенсивности напряжений АКр
AKI = KI, max - KI, min = (°1, max - °1, min) ' 11/2 ' Y
В этой формуле CT1max и ст1, min — средние по достаточно большому объему материала с трещиной главные нормальные напряжения, а Y — коэффициент K-тарировки для этой трещины.
Математически моделировать задачу об образовании и росте малых трещин очень сложно, так как нужно знать механические свойства отдельных зерен с учетом их ориентировки, неизотропно - сти и уметь вычислять локальные напряжения и локальные деформации в них. Поэтому стадию образования и роста малых трещин при технических расчетах относят к стадии зарождения усталостного разрушения, завершение которой определяют экспериментально по появлению на образце или детали трещины с расчетной длиной 2-3 мм.
Дальнейшее распространение такой трещины рассчитывают с использованием линейной механики разрушения.
На третьей стадии, когда усталостная трещина достигает критического размера, выполняется условие статического разрушения, например, KI = KIC. Тогда происходит статический долом детали по механизму либо хрупкого, либо вязкого, либо смешанного «ква - зихрупкого» разрушения, когда отдельные участки хрупкого излома детали сменяются участками вязкого излома и наоборот.