ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
УПРОЧНЕНИЕ НА РАСТВОРЕННЫХ АТОМАХ
5.2.1.
ОСЕСИММЕТРИЧНАЯ СФЕРИЧЕСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
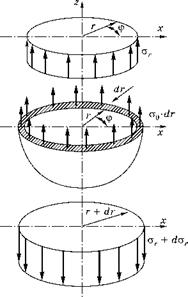
Рассмотрим равновесие половины малого симметричного сферического элемента, изображенного на рис. 5.16.
Сферические координаты: r — радиус; ф — угол азимута (долгота на глобусе); 0 — угол места (широта на глобусе).
Выделим сферический тонкостенный элемент с внутренним радиусом r и наружным радиусом r + dr. Рассечем этот элемент по
диаметру 0 = 0. Получим сферическую чашу, изображенную в средней по высоте части рис. 5.16. Для нее составим уравнение проекций всех сил на ось 2.
|
Рис. 5.16 Расчетная схема уравнения равновесия для половины малого сферического элемента |
Проекция напряжений ar, действующих на всей внутренней поверхности элемента, равна этим напряжениям, умноженным на площадь проекции внутренней поверхности на плоскость, перпендикулярную оси 2. Эта эпюра изображена в верхней части рисунка, и сила от нее составляет: N2 = ar - л - г2.
При увеличении радиуса r на малую величину dr напряжения ar получают приращение dar. Поэтому проекция на ось 2 равнодействующей радиальных напряжений, действующих на наружную поверхность элемента, равна:
(N2 + dN2) = (ar + dar) - л - (r + dr)2.
Эпюра, создающая эту силу, показана в нижней части рисунка. Напряжения сте, действующие в диаметральном сечении стенки элемента, создают погонную силу, равную aedr. Эпюра этой силы изображена в средней части рисунка. Ее равнодействующая:
N2e = сте - 2 -л - r - dr.
Суммируя все перечисленные силы, получим уравнение равновесия для половины сферического элемента:
£ Z = 0 = N - (N + dNz) + N2,=
= ar - n-r2 -(ar + dar)-n-(r + dr)2 +ct0 • 2n •r dr = 0.
Сокращая на л, раскрывая скобки, пренебрегая малыми величинами второго и третьего порядка и уничтожая члены (-стг - лг2 + + ar ■ лг2), получим:
ar - 2r - dr + dar - г2 - сте - 2r - dr =0.
После деления этого выражения на г2 - d, получим дифференциальное уравнение равновесия с двумя (ar и сте) неизвестными функциями от r:
dQr + 2(pr ~р8 ) = 0 dr r
|
(5.21) |
Чтобы получить из (5.21) обыкновенное дифференциальное уравнение, нужно выразить напряжения через радиальное перемещение uk. При записи закона Гука учтем, что в силу сферической симметрии
|
^8 ; ^8 r ; ^r |
dur dr '
Тогда уравнения закона Гука примут вид:
sr = E' [°r _V' (СТФ +СТе )] = E' [°r _ 2v-ct9 ] = dr;
|
ф |
|
ф |
|
E |
|
E |
|
єф = 1 -[СТф - V'(CT0 + CTr )] = — '[(1 - V) - СТф - V'CTr ] = ~r. |
Решим эту систему из двух уравнений относительно напряжений: d
°r -2v' СТФ = E' ~r;
-v' Or + (1 - v)' СТф = E' Ur;
|
откуда следует: |
|
стф = CTe = C ■ |
|
(5.22) |
|
стг = C |
|
(1 - v) .^- + 2v u dr r |
|
. dUr + u dr r du. |
|
где |
|
E |
C = -
1 - v-2v2
Подставим формулы (5.22) в уравнение (5.21):
|
d2ur |
|
C ■ |
|
(1 - v) |
|
dr 2 dur |
|
2C r |
|
(1 - v) |
|
= 0. |
|
dr |
|
Q I 1 d ur 1 -2v-|----------- - u ■ — r dr r2 -2v ■ u-v ^ - u r dr r |
Сократив на С ■ (1 - v), получим обыкновенное дифференциальное уравнение сферически симметричной задачи:
|
(5.23) |
d2ur + 2 dur _ 2u _ о dr2 r dr r2
Его решение будем искать в виде степенной функции: ur = A ■ rn, где: A, n — постоянные. Вычислим производные этого решения:
— = A ■ n ■ rn 1;
|
du dr d2u |
L = A ■ n ■ (n -1) ■ rn-2.
dr 2
После подстановки этих производных в уравнение (5.23) получим:
A ■ n ■ (n -1) • rn-2 + — • A ■ n ■ rn-1 - -—- ■ A ■ rn - 0, r r2
или после сокращения на A ■ rn-2:
n ■ (n -1) + 2 • n - 2 = 0; ^ n2 + n - 2 = 0; ^
ni,2 =-2±^(-1) -(-2) =-0,5±1,5;^
ni = 1,0; n2 = -2,0.
Двум решениям (n1 и n2) соответствуют два значения постоянной А. Общее решение уравнения (5.23) получается в виде суммы
|
A, |
|
г2 ’ |
этих решений:
(5.24)
где постоянные A1 и А2 определяются из граничных условий.