ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
СИЛА, ДЕЙСТВУЮЩАЯ НА ДИСЛОКАЦИЮ
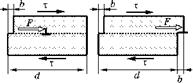
На рис. 4.8 показана часть кристалла единичной толщины, нагруженная напряжениями т с одной краевой дислокацией.
Дислокацию перемещает приложенная к ней погонная сила F. В момент появления дислокации на левой грани кристалла образуется уступ шириной b, показанный на левом рисунке. После перемещения дислокации на расстояние d на правой грани появляется соответствующий уступ, показанный на правом рисунке. В силу
|
Рис. 4.8 Схема работы силы F, действующей на краевую дислокацию |
закона сохранения энергии работа, совершенная силой F на перемещении дислокации d, должна быть равна работе напряжений т, действующих на площади d ■ 1, на перемещении b верхней части кристалла относительно нижней. Запишем это равенство:
F ■ d = (т - d) ■ b, откуда сила, действующая на дислокацию:
F = т-b. (4.22)
Винтовая дислокация будет перемещаться в перпендикулярном действию т направлении. Но результат для силы F сохранится. В этом читатель может самостоятельно убедиться, построив соответствующий рисунок.
4.2.6.
СИЛА ВЗАИМОДЕЙСТВИЯ ДИСЛОКАЦИЙ
Погонная сила взаимодействия между двумя дислокациями вычисляется как производная от упругой энергии суммарного поля напряжений по расстоянию между ними. С вычислениями можно ознакомиться в учебнике Ж. Фриделя «Дислокации». Здесь приведем лишь некоторые результаты.
Взаимодействие дислокаций похоже на взаимодействие электрических зарядов: одноименные отталкиваются, противоположные — притягиваются.
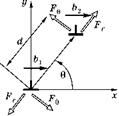
Две винтовые дислокации с параллельными векторами Бюргерса b1 и b2, расположенные на расстоянии d друг от друга (рис. 4.9), взаимодействуют с погонной силой:
G • b • b2
|
Fr =- |
(4.23)
2 •n^d
|
Рис. 4.9 Силы взаимодействия дислокаций |
|
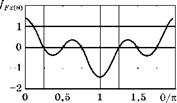
Рис. 4.10 Зависимость силы Fx от угла ( |
При выводе этой формулы первая дислокация помещена в начало координат. Вторая дислокация находится в точке с полярными координатами d, 0 (рис. 4.9). Для винтовых дислокаций векторы Бюргерса на рис. 4.9 должны изображаться точками, так как они ориентированы вдоль оси 2.
Для двух краевых дислокаций выражения для вычисления проекций силы взаимодействия имеют вид
G ■ h ■ Ъ2 ,
Fr =
|
(4.24) |
2 ■ (1 - v) ■%■ d’ G ■ Ъ ■ Ъ2
|
Ffl = |
sin(20).
2 ■ (1 - v) ■%■ d
Но краевая дислокация может двигаться только в плотноупа - кованной плоскости скольжения в направлении оси x (рис. 4.9). Силу Fx, вызывающую движение краевых дислокаций, можно вычислить, суммируя проекции сил Fr и F0 на ось х:
|
G ■ h ■ Ъ2 f cos(0) ■ cos(20) |
|
(4.25) |
|
1 - v |
|
Fx = Fr ■ cos(0) - F0 ■ sin(0) = - |
|
2n^d |
Функция от угла 0 имеет вид
cos(0) ■ cos(20)
|
(4.26) |
fFx (0) =-
(1 - v)
Ее график показан на рис. 4.10.
Из рисунка видно, что при 0<п/4 дислокации одинакового знака отталкиваются, разного знака — притягиваются. При углах 0 > п/4 все наоборот. Дислокации одинакового знака будут находиться в устойчивом равновесии при углах 0, равных п/2 и 3п/2. Для дислокаций разного знака устойчивое равновесие будет при углах п/4, 3п/4, 3п/2.
Силу взаимодействия дислокаций со свободной поверхностью можно описать формулами (4.24). Для того чтобы разгрузить
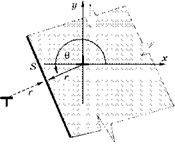
поверхность от напряжении, вызванных заданной дислокацией, достаточно зеркально к ней поместить такую же дислокацию противоположного знака (рис. 4.11).
|
Рис.4.11 Схема определения силы взаимодействия дислокации со свободной поверхностью S |
Видно, что сила взаимодействия дислокации с поверхностью равна силе взаимодействия между двумя дислокациями противоположных знаков, расположенными в направлении нормали к поверхности и на расстоянии г, равном удвоенному расстоянию до поверхности.
Винтовые дислокации всегда притягиваются к свободной поверхности. Краевые дислокации притягиваются к свободной поверхности не всегда (см. рис. 4.10).