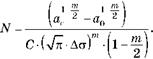ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
РАСЧЕТ РОСТА ТРЕЩИН УСТАЛОСТИ
Содержание разделов 6.4.1-6.4.3, строго говоря, относится только к анализу условий зарождения трещин усталости. Хотя в эти разделы попали экспериментальные результаты ранних работ, в которых две стадии усталостного разрушения: зарождение (инициация, initiation) трещины (число циклов — N;) и распространение (рост, propagation) усталостной трещины (число циклов — Np) — не различались. Испытания на выносливость в этих работах всегда доводились до полного разрушения. Поэтому в них сообщалось только число циклов до полного разрушения Nf = Nt + Np. Эту особенность нужно обязательно учитывать при использовании литературы.
Процесс роста усталостной трещины с приведенной длиной дефекта а обычно изображается в координатах:
■ ордината da/dN — величина подрастания трещины за 1 цикл нагрузки;
■ абсцисса AKI — размах коэффициента интенсивности напряжений для трещины нормального отрыва, который вычисляется на основании формулы (3.87):
|
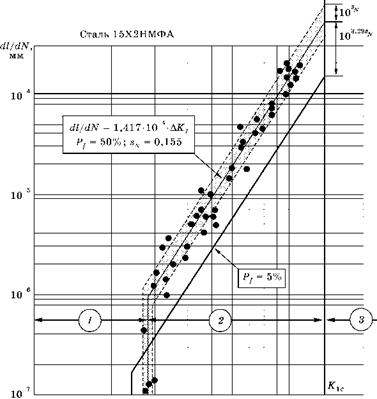
AKi = (ACT)-4кУа = (<7max “ ^ min) ' . Экспериментально установлено, что в двойных логарифмических координатах зависимость da/dN от размаха коэффициента интенсивности напряжений AK имеет вид, представленный на рис. 6.94.
юо дKth юоо &к Рис. 6.94 Зависимость скорости роста трещины от AK, Н/мм3/2 |
На этом рисунке три области. В первой при AKI < AKthтрещина не растет и da/dN = 0 (индекс th от threshold — анг. «порог»). Следовательно, AKth — пороговое значение размаха коэффициента интенсивности напряжений.
Во второй области зависимость скорости роста усталостной трещины от AKj в двойных логарифмических координатах практически линейна. Это значит, что она описывается степенным законом:
|
|
(6.190)
где С и m — постоянные материала.
Наконец, в третьей области происходит катастрофическое распространение хрупкой трещины, как при статической нагрузке,
|
|
|
max |
|
когда |
|
KI, max |
(6.191)
Среднеквадратичная полоса разброса экспериментальных точек на рисунке затемнена точками. Центральная наклонная линия этой полосы (при вероятности разрушения Pf = 50%) вычислена при линейной регрессии экспериментальных точек в логарифмических координатах. Полученное уравнение показано в выноске, там же указано среднеквадратичное (в логарифмических координатах) отклонение экспериментальных точек от этой линии: sN = 0,155. Жирной сплошной наклонной линией на рисунке показана граница с вероятностью разрушения Pf = 5%, которая в соответствии с рис. 6.77 получается из линии для Pf = 50% путем деления ее ординат на 103,29sN. В логарифмических координатах это деление сводится к сдвигу линии вниз на 3,29sN.
При приближенных расчетах подрастания усталостной трещины, если значение AKth неизвестно, в запас долговечности наличием зоны I можно пренебрегать, считая AKth = 0.
Эффективный размер дефекта а вычисляется по действительной длине дефекта l по формуле (3.86). В этой формуле Y — коэффициент K-тарировки, зависящий от формы трещины и отношения длины трещины l к характерному размеру опасного сечения детали b. Таким образом, Y изменяется по мере роста трещины. Учет этого обстоятельства приводит к необходимости при вычислении роста трещины переходить к численному интегрированию. Однако если ожидаемое приращение трещины Аа мало по сравнению с характерным размером сечения b, то изменением Y можно пренебречь. Тогда, используя формулу (6.190), можно записать:
|
(6.192) |
ddN = с • (Act)m.
После разделения переменных это уравнение примет вид
|
(6.193) |
a 2 • da = C • (л/л-Лст)т • dN.
Интегрируя обе части уравнения от а0 до ас и от 0 до N, при m Ф 2, получим
|
ac 2 _ a0 2 |
1_m 1_m
|
|
C-(V^-ЛстГ • N
или
|
|
При m = 2 решение уравнения (6.193) примет вид
lna = C-(V^-ЛстГ • N, a0
0
откуда для числа циклов получим выражение
N = ln(ac / ap) C -(Vn-A a)
Экспериментально определенные постоянные, входящие в формулу (6.190), взятые из монографии Г. П. Карзова, В. П. Леонова и Б. Т. Тимофеева «Сварные сосуды высокого давления», приведены в табл. 6.17.
Параметр С95%, приведенный в трех нижних строках этой таблицы, соответствует верхней границе полосы разброса экспериментальных точек при вероятности разрушения Pf = 95%. Для определения С50% и m использован метод линейной регрессии. Эти параметры дают линию посередине поля разброса экспериментальных точек при вероятности разрушения Pf = 50%. В частности, сплошная наклонная прямая на рис. 6.94 построена по С50% и m, взятым из третьей снизу строки этой таблицы, а пунктирная наклонная прямая соответствует С95% из этой же строки. Из таблицы видно, что С95% во всех случаях примерно в два раза превышает величину параметра С50%.
Параметр a0 (начальная длина трещины) обычно неизвестен. В этом случае его принимают равным минимальному размеру дефекта, который уверенно может обнаружить принятая для контроля качества швов аппаратура. Кроме этого в формулу (6.193) вводят коэффициенты запаса по критической длине трещины ас около 2, и по критическому числу циклов нагрузки Nc около 10.
|
Таблица 6.17 Параметры роста усталостных трещин (размерность С— кН/мм3/2)
|
Тогда, используя выражение для определения критического размера трещины
KIC - CTmax • Vп 'ac
или
1 Г Kic
^ V ^mj
можно формулу (6.193) представить в виде
-|1-т/2
|
1-m/2 0 |
- a,
2п [ а
|
(6.194) |
Nc =
10 • C ' [(amax - amin) 'V^] '(l -
Например, для сосуда из малоуглеродистой ферритно-перлитной стали (С = 4,17-10-5; m = 2,22) при Kic = 300 кгс/мм3/2 = 3 кН/мм3/2, при пульсирующем цикле нагружения CTmin = 0 и amax = 10 кгс/мм2 =
= 100 Н/мм2 = 0,1 кН/мм2, при начальном размере дефекта а0 = = 5 мм, получим, что допустимое число циклов нагрузки составляет
-|1—2,22/2
|
2л I, 0,1 |
51—2,22/2
Nc ------------- L~" — J —------------------------------------------ = 2,6 • 105.
Г і—п2,01
10• 4,17 10_5 {(0,1 _0)•лЫ • (1 _2,22/2)
Если убрать из этой формулы коэффициенты запаса, то при вероятности разрушения Pf = 50% число циклов до разрушения будет равно 3,06 106.
Замечание. Широко используемая в литературе формула (6.190) имеет существенный недостаток. Поскольку показатель степени т в этой формуле обычно не целое число, то постоянная С имеет размерность мм [кГ/мм3/2]-т и/или мм [Н/мм3/2]-т. И сила, и длина в этой размерности в абсурдной степени. Чтобы устранить этот недостаток, некоторые авторы справедливо предлагают записывать эту формулу в виде:
da 0_5 (ДКі
dN 10 ' ДК0 J, (6.190а)
в которой постоянная 10-5 имеет размерность длины, а постоянная материала АК0 входит с привычной для коэффициента интенсивности напряжений размерностью [кГ/м3/2].