ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ПОЛЯ НАПРЯЖЕНИЙ У ДИСЛОКАЦИЙ
Около винтовой дислокации (рис. 4.5а) единственные перемещения uz образуют винтовую линию:
А • r
u=b • • (4Л2>
Координаты r и 0 показаны на рис. 4.5в.
Обходя вокруг винтовой дислокации по кристаллографической плоскости, можно подниматься, как по винтовой лестнице, на b за каждый оборот.
Сдвиговая деформация хорошо видна, если начертить развертку цилиндра с произвольным радиусом г. Она равна высоте подъема линии перемещений за один оборот к длине окружности:
|
(4.13) |
|
Y ze = |
b
2-n-r'
|
|
|
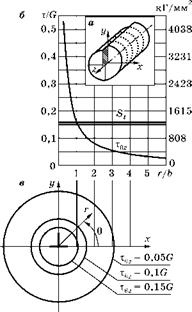
Рис. 4.5 Распределение напряжений у винтовой дислокации |
|
Единственные не равные нулю напряжения TQz распределены осесимметрично: |
|
G ■ b 2■n^r' |
|
= G-Iz0 = |
|
(4.14) |
|
Z0 |
|
Радиальное распределение этих напряжений представлено в виде графика на рис. 4.56. На правой шкале напряжения отнесены к модулю сдвига G. На левой указаны численные значения напряжений для железа. Шкала радиусов дана в межатомных расстояниях b. На этот график нанесена горизонтальная прямая теоретической прочности при сдвиге, определенной выше по формуле (4.9). Видно, что теоретическая прочность на сдвиг у дислокации достигается уже на расстоянии одного межатомного промежутка от линии дислокации. В этой зоне, где превышена теоретическая прочность, расчеты напряжений по обычным методикам не имеют смысла. Эта зона называется ядром дислокации или областью «плохого кристалла». На рис. 4.5в показана система декартовых и цилиндрических (r, 0, z) координат и проведены три изолинии поля напряжений с привязкой масштаба по оси x к рис. 4.56. Касательные напряжения, равные пределу текучести (для стали тТ = 12 кГ/мм2), достигаются на расстоянии от линии дислокации: |
|
2,1 -104 |
|
G - b |
|
E - b |
|
-Ъ —107 - b. |
|
Гг — |
|
2 - л-тт 2 - л-2 -(1 + v) - тт 4 - л-1,3 -12 |
|
Это достаточно большое расстояние по сравнению с аналогичным расстоянием поля от внедренного атома или вакансии. Поэтому поля напряжений от дислокаций называют дальнодействующими. При расчетах взаимодействия дислокаций удобнее поле напряжений (4.14) записать в декартовых координатах: |
|
G ■ b |
|
G ■ b |
|
У |
|
(4.15) |
|
■л X2 + У2 |
|
■л X2 + У2 |
Поля напряжений у краевой дислокации в полярных координатах вычисляются по более сложным формулам:
|
sin(0) (T-V) |
|
G - b 2-n-r |
|
G - b 2-n-r |
|
fr (0); |
|
аг — Ста — |
|
G - b |
|
(1 - v) G - b |
|
(4.16) |
|
G - b 2-n-r |
|
fzz (0). |
|
2-n-r |
|
12-n-r az — v-(^ +^0) — |
|
cos(0) |
|
Tr0 — |
|
G - b 2-n-r, 2 - v-sin(0) (1 - v) |
|
fr0 (0); |
Первый сомножитель в фигурных скобках этих формул повторяет правую часть формулы (4.16) для винтовой дислокации и задает форму кривой распределения напряжений по радиусу. Ее график дан на рис. 4.56. Вторые сомножители представляют функции от угла 0, различные для различных напряжений.
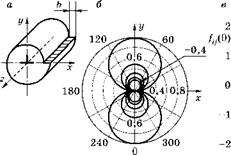
На рис. 4.6 показана схема задачи о напряжениях у краевой дислокации (а), изолинии гидростатических напряжений ат, от
|
для расчета |
|
Рис. 4.6 Схема краевой дислокации (а); изолинии om/(G ■ b) (б) и функции угла 0 для напряжений ау (в) |
|
|
несенных к G ■ b с шагом 0,2 (6), и функции от угла ( напряжений (в).
|
У |
Мй |
) = / |
»(У) |
|||||
|
' |
/ / |
й(0> |
||||||
|
_ |
/ |
п |
||||||
|
" |
/V |
|||||||
|
N |
ч fгб( |
|||||||
|
0 1/4 1/2 3/4 1 5/4 3/2 7/4 2 0/71 |
Из рисунка видно, что при положительных значениях координаты у гидростатические напряжения отрицательны, а при отрицательных у они положительны. Изолинии этих напряжений представляют собой окружности, касающиеся оси х в точке расположения дислокации (х = 0; у = 0).
Для справки ниже приведены формулы для вычисления напряжений у краевой дислокации в декартовых координатах.
СТ* = (2 G/ ) !• [■ sin(0)• (2 + cos(20))]- 2 G(l> ) • • 23х2^22);
(2 л(1 - v) r 2 л(1 - v) (х2 + у2)2
°у - ( — ) !• [sin(0) • cos(20)] - 2 G:> ) • у (2х2 ~?2;
у (2 л(1 -v) r 2 л(1 - v) (х2 + у2)2
f G • b ) г, OQV1 G • b X • (х2 - у2)
тху - —----- (r[cos(0)• cos(20)]------------- ------- -• —^----- ^ji.
у (2 л(1 - v) r 2 л(1 - v) (х2 + у2)2
(4.17)