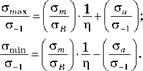ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ПОЛНАЯ ДИАГРАММА ГУДМАНА
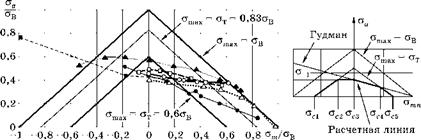
Диаграмма рис. 6.78а построена только для области cm > 0. При построении полной диаграммы нужно учесть и область средних сжимающих напряжений. Экспериментальные результаты по влиянию средних напряжений c m на амплитудные напряжения предела усталости c а для трех сталей низкой и средней прочности и трех сталей высокой прочности приведены на рис. 6.79[6].
Внешний треугольник, очерченный двумя жирными прямыми, соответствует условиям - c min = c B и c max = c B. При положительном среднем напряжении экспериментальных точек за преде-
|
|
|
Обозначение |
Химический состав |
Автор |
Год |
|
|
о----------- |
41,5 |
0.1С |
Гаф |
1939 |
|
Д.......... |
46,4 |
0.13С; 0.6Мп |
Тейлор |
1941 |
|
□--- |
49,2 |
0.16С; 1Мп |
Тейлор |
1952 |
|
•----- |
80,8 |
3.6Ni; 0.6Сг |
Ли |
1924 |
|
А..................... |
87,9 |
2.5Ni; 0.6Сг |
О’Коннор |
1956 |
|
■--- |
90,0 |
SAE4640 |
Финдли |
1954 |
|
Рис. 6.79 Зависимость предельных амплитудных напряжений от средних напряжений для различных сталей (слева) и схема построения расчетной ломаной линии для амплитудных напряжений (справа) |
лами этого треугольника быть не должно вследствие разрушения образцов при статической нагрузке. Поэтому две экспериментальные точки в виде черных треугольников, вышедших за пределы этой прямой, можно объяснить только небольшим отклонением действительного предела прочности образцов от марочного значения. При отрицательном среднем напряжении потери устойчивости пластических деформаций при cmin = - aB не происходит. Поэтому появление двух черных экспериментальных точек (квадрат и треугольник) левее данного условия вызывает удивление только с точки зрения методики испытаний на усталость при столь больших амплитудах пластических деформаций.
Внутри этого внешнего треугольника построены еще два треугольника, приближенно характеризующие условие текучести (°min = -°т и amax = стт). Пунктирными линиями нанесен треугольник для с0,2 = 0,83сВ, что похоже на сталь HT80 с пределом прочности 80 кг/мм2 и относится к черным экспериментальным точкам. Внутренний треугольник отображает условие текучести при °0,2 = 0,6аВ, что похоже на стали с низкой и средней прочностью (светлые точки).
Из рисунка видно, что около половины всех экспериментальных точек лежат за ориентировочными границами текучести. Вероятно, они относятся к области малоцикловой усталости. Кроме того, экспериментальные точки только одной высокопрочной стали, представленные черными кружками, достаточно хорошо ложатся на диаграмму Гудмана. Линии для остальных сталей лежат выше. В области отрицательных средних напряжений у некоторых сталей наклон линии весьма невелик.
Обычно в расчетных нормах для всех сталей используется единая зависимость расчетных амплитудных напряжений от средних напряжений. Такую зависимость нужно построить по нижней границе экспериментальных точек рис. 6.79 — ее схема показана в правой части рисунка жирной ломаной линией. При положительных ат расчетная зависимость соответствует диаграмме Гудмана, но ограничивается условием текучести в виде более крутого отрезка прямой справа. При отрицательных ат расчетная линия горизонтальна (оа = ст_!) и ограничивается слева более крутым отрезком прямой по условию CTmin = - стт.
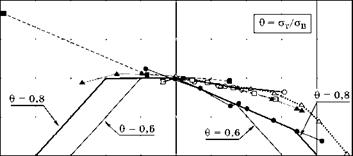
Более подробно такое построение выполнено на рис. 6.80, где амплитудные напряжения по оси ординат отнесены не к пределу прочности, а к пределу усталости при симметричном цикле.
Поэтому все экспериментальные точки рис. 6.79, полученные при ат = 0, здесь слились в одну точку. Кроме линий схемы из левой части предыдущего рисунка с ограничениями по пределу текучести при 0 = ст-1/ств = 0,6 и 0 = 0,8 также нанесены все экспериментальные точки. Видно, что диаграмма предельных амплитудных напряжений достаточно хорошо описывает нижнюю гра-
|
|
|
°-i |
|
1,5 1,0 |
|
0,5 |
|
0 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 оп/ав |
|
Рис. 6.80 Приведенная диаграмма предельных амплитудных напряжений и экспериментальные точки рис. 6.79 |
ницу разброса экспериментальных точек и состоит из четырех прямолинейных участков:
1. °min = - Стт или ат - <за = - Стт, откуда стд/ст_1 = (0 + ат/ав)/ц.
2. а а = СТ_1 или Ста/ст_1= 1.
3. а а = а_1 - (ст_1/СТв) • От или Оа/О-1 = 1 - (СТт/СТв).
4. Omax = От или От + а а = СТ^ откуда Оа/О-1 = (0 _ От/Ов)/Л.
Диаграмма содержит пять критических значений средних напряжений, которые показаны на правой схеме рис. 6.79 и обозначены ас. Величины этих напряжений можно получить на основании следующих соображений:
■ амплитудные напряжения не могут быть меньше 0, поэтому по первой формуле получим ас1 = - и • ав;
■ во второй точке аа по первой и второй формулам равны: (0 + + аС2/ов)/л = 1, откуда следует аС2 = (1/л - 0) • а в;
■ в третьей точке средние напряжения равны нулю: ас3 = 0;
■ в четвертой точке амплитудные напряжения по третьей и четвертой формулам составляют 1 - ас4/ав = (0 - ас4/ав)/л; откуда ас4 = (л - 0) • ав/(1 • л);
■ в четвертой формуле амплитудные напряжения не могут быть меньше 0; откуда ас5 = и • ав.
|
|
|
Зная амплитудные напряжения, нетрудно определить максимальные и минимальные напряжения по формулам: |
|
(6.174) |
|
|
|
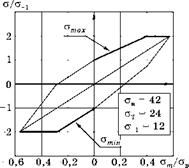
Используя формулу (6.163) и выражения из табл. 6.10, можно вычислить полную диаграмму Гудмана (рис. 6.81). При этом приняли значения механических свойств стали, указанные на поле рисунка, близкие к свойствам стали ВСт3. ЭЛЕКТРОННАЯ БИБЛИОТЕКА |
В итоге, диаграмма предельных амплитудных напряжений описывается формулами табл. 6.10.
|
Таблица 6.10 Формулы диаграммы предельных амплитудных напряжений
|
При положительных средних напряжениях расчетным напряжением является amax, а характеристика цикла вычисляется по формуле: r = CTmax/amin. При отрицательных — расчетным напряжением является - amin, а характеристика цикла вычисляется по формуле: r = - CTmin/amax. Расчетные напряжения показаны на рис. 6.81 жирными отрезками прямых линий.
|
Рис. 6.81 Полная диаграмма Гудмана |
В нормах расчета (например, СНиП) влияние средних напряжений учитывается коэффициентом у. Используя приведенные выше формулы (6.174) для (сттах/ст-1) и (-сттіп/ст-1), а также выражения из табл. 6.10, нетрудно получить выражения для коэффициента у:
|
У |
(6.175)
1
Они приведены в табл. 6.11, где для сравнения даны формулы для расчета коэффициента у, рекомендуемые СНиП, который задается как функция от характеристики цикла r отдельно для области сжимающих средних напряжений и отдельно для области растяжения.
|
Таблица 6.11 Формулы для расчета коэффициента у
|
Результаты расчета коэффициента у по формулам табл. 6.11 графически представлены на рис. 6.82.
|
СНиП; |
°т>0 |
1 1 1 |
/ / |
|
СНиП; |
°т< 0 |
У/ |
/ |
|
°П |
.<0 |
у/А |
/г| = 2 |
|
™>о |
|
-1 -0,5 0 0,5 Рис. 6.82 Графическое представление формул табл. 6.11 |
Двумя жирными сплошными кривыми линиями показаны результаты, вычисленные по полной диаграмме Гудмана (для ат > 0 и ат < 0) c ограничением коэффициента у (по условию текучести) значением 0/г| = ат/а_! = 24/12 = 2. Прерывистыми линиями показаны аналогичные результаты вычислений по формулам, рекомендуемым СНиП.
Эти формулы не имеют ограничений по пределу текучести, так как условие недопущения текучести металла в СНиП устанавливается отдельным расчетом конструкции на статическую нагрузку.
Из рисунка видно, что без учета ограничений по текучести при ат <0 расчет у по обобщенной диаграмме Гудмана совпадает с расчетом по СНиП. Однако при ат >0 расчетная прерывистая кривая по СНиП располагается выше, чем сплошная кривая, рассчитанная по Гудману. Это связано с тем, что формулы СНиП при вычислении коэффициента у предполагают, что амплитудные напряжения и при ат >0 остаются постоянными и не зависят от средних напряжений цикла.