ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ПОДХОД, ОСНОВАННЫЙ НА НОМИНАЛЬНЫХ НАПРЯЖЕНИЯХ
Подход, основанный на номинальных напряжениях, включен в следующие нормативные документы:
• британские стандарты: BS7608, BS5400, BS5500, BS8118,
BSPD6493 (1980-1991 гг.);
• американский стандарт по расчету котлов и сосудов ASME 1968 г.;
• руководство по расчету сварных соединений Международного института сварки (IIW) 1990 г.;
• европейские стандарты ECCS/SECM/TKS 1985 и 1992 гг.;
• стандарт Eurocode 3 по расчету стальных конструкций 1992 г. На этом подходе также основан расчет металлоконструкций
на усталость, рекомендованный в СНиП 1990 г.
Расчетные амплитудные номинальные напряжения ona должны быть меньше допускаемых напряжений [ana]:
°na * Ka], (6.195)
которые находятся путем деления экспериментального значения предела выносливости ana50 при вероятности разрушения Pf = 50% на коэффициент запаса по напряжениям:
Ka ] = J-. (6.196)
Jg
|
■ J Ne 'na50 I n |
Экспериментальное значение предела выносливости ana50 как функции от числа циклов N определяется на основании линейной регрессии экспериментальных точек в координатах log(ana50) - log(N) по формуле
■OnE. (6.197)
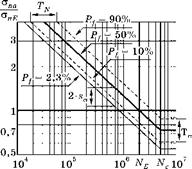
Здесь ja — коэффициент безопасности, определенный по рис. 6.77 для европейских норм при Pf = 2,3% по формуле:
ja= 102sn,
где sN — среднеквадратичное отклонение экспериментальных точек от линейной (в логарифмических координатах) зависимости (6.197); Ne — число циклов, при определении предела усталости (обычно Ne = 2106 циклов); стпЕ — экспериментальный предел усталости материала по формуле (6.197) при числе циклов NE и вероятности разрушения Pf = 50%.
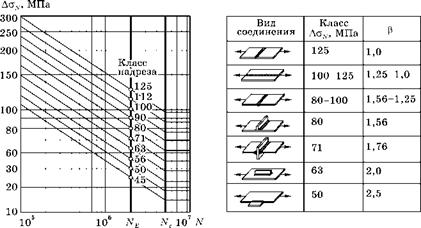
В качестве примера на рис. 6.95 приведены некоторые данные из рекомендаций Международного института сварки (IIW) для соединений, выполненных сваркой плавлением.
Все соединения в зависимости только от формы, разбиты на 10 классов. Класс характеризуется значением допустимого размаха номинальных напряжений Аст. На рис. 6.95 классы показаны малыми светлыми кружочками и цифрами на соответствующих каждому классу наклонных линиях. Цифра класса определяется как Асткласса = 2[СТпе] = 2anE/Ja, где j = 102sN определен с учетом
|
Рис. 6.95 Классы надреза сварных соединений конструкционных сталей по рекомендациям МИС 1982 г. Ne = 2106; Nc = 5106; k = 3,5. |
допустимой вероятности разрушения Pf = 2,3% (рис. 6.77), а стпЕ определено при числе циклов N = Ne = 2106 и Pf = 50%.
Все наклонные линии имеют тангенс угла, равный (-1/k), где k = 3,5. Все наклонные линии продолжаются до критического числа циклов Nc, при котором достигается нормативный физический предел усталости, и Аст перестает зависеть от числа циклов.
В правой части рис. 6.95 дана таблица, в которой приведены схемы некоторых сварных соединений, цифрами указаны значения классов. В последней колонке этой таблицы приведены значения эффективных коэффициентов концентрации р. Они в стандарт не входят и вычислены мной путем деления значения Асткласса на 125 (Р = 1).
По рекомендациям IIW сопротивление усталости Аст не зависит от прочности стали, от средних напряжений стт и характеристики цикла r = сттіп/сттах.
На рис. 6.96 приведена нормализованная диаграмма по европейским нормам Eurocode 3 (1992).
|
ь ПАШ? |
Здесь ординаты графика рис. 6.95 поделены на экспериментальный предел усталости стпЕ для каждого класса, поэтому все линии графика слились в одну. По сравнению с рекомендациями IIW в Eurocode 3 изменен наклон линий: k = 3,0. Кроме того, в качестве основной линии дана зависимость для вероятности разрушения Pf = 50%, а требуемую вероятность разрушения при расчетах поль-
ЭЛЕКТРОННАЯ БИБЛИОТЕКА
|
|
|
Рис. 6.96 Нормализованная кривая для расчета сварных соединений конструкционных сталей на усталость по Eurocode 3: к = 3,0; Та =1:145; Tn =1:3; anE = = (1 - r) ■ а„2/2; ana = °nE ■ (NE/N)1/k. |
|
зователь норм может устанавливать самостоятельно по заданной нормами ширине полосы разброса экспериментальных точек T: |
|
1 3, |
|
jg10 |
|
Tn = (T )к = |
|
Т„=- |
|
1,45’ |
|
где ста10 — нижняя граница полосы разброса экспериментальных точек при вероятности разрушения Pf = 10%; ста90 — верхняя граница полосы разброса экспериментальных точек при вероятности разрушения Pf = 90%. Как и в рекомендациях IIW экспериментальный предел усталости onE определяется по классу формы сварного соединения, но для Pf = 50%. Чтобы воспользоваться рис. 6.77 для определения запаса прочности j по величине нормального среднеквадратичного отклонения по напряжениям sa и по числу циклов sN, приведенные здесь значения ширины полосы разброса Та и TN следует пересчитать на среднеквадратичные отклонения: |
|
2,56 'l0gITc |; |
|
log І7^|. |
|
s„ - |
|
Sn — ■ |
|
2,56 |
Кроме этого в Eurocode 3 предусмотрено ограничение максимальных напряжений цикла пределом текучести:
_ < (1 - r) _
ana < 2 'СТ0,2,
но считается, что допускаемые номинальные амплитудные напряжения от средних напряжений цикла не зависят. В результате при допуске на вероятность разрушения Pf = 2,3% запас прочности по рис.6.77 составит
2
j = 102s = Ю256'log(1,45) = 1,337, и допускаемые номинальные амплитудные напряжения по формулам (6.196) и (6.197):
|
1/k |
|
Ne N |
|
Jna50 |
|
1,337 |
|
JnE |
|
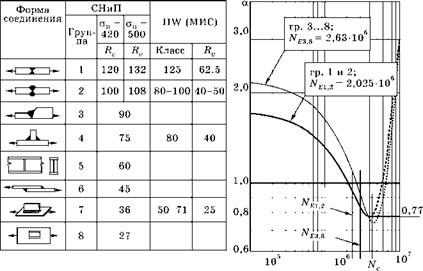
Рис. 6.97 Группы сварных соединений по СНиП, расчетные сопротивления и их зависимость а от числа циклов нагружения N: |
°max Sa-У Rv'; Nc = 3,9106
На рис. 6.96 граница допускаемых напряжений показана сплошной ломаной линией со сноской Pf = 2,3%, которая сдвинута на 2sa вниз относительно средней линии c Pf = 50%.
В CНиПах вместо 10 классов IIW (рис. 6.95) сварные соединения сварки плавлением разбиты на 8 групп, схемы представителей которых показаны в первой колонке таблицы рис. 6.97.
В этой таблице приведены номера группы и расчетное сопротивление при усталости Rv, МПа. Rv — допускаемые номинальные амплитудные напряжения при знакопеременном цикле (г = -1) и числе циклов до разрушения N = NE.
В общем случае максимальное номинальное допускаемое напряжение цикла по СНиП вычисляется согласно формуле
[°max] = а'У'
где а — коэффициент, учитывающий влияние числа циклов, вычисляется по формулам (6.168); его зависимость от числа циклов N показана на графике рис. 6.97; у — коэффициент, учитывающий влияние средних напряжений ат или характеристики цикла г.
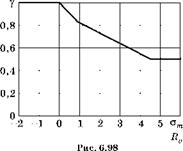
Зависимость у от ат показана на рис. 6.98.
Сопоставляя этот график с зависимостью амплитудных напряжений цикла от средних напряжений по диаграмме Гудмана, видно, что зависимость на рис. 6.98 существенно слабее при растяжении и такая же при сжатии средними напряжениями. В рекомендациях IIW и в Eurocode 3 аналогичная зависимость отсутствует. Но в СНиП не указана зависимость допускаемых напряжений от ширины полосы разброса экспериментальных точек и от допуска на вероятность разрушения Pf.
|
Зависимость коэффициента у от средних напряжений |
|
No jN |
Расчет долговечности по европейским нормам основан на вероятности
|
(6.198) |
N < [N]; [N] =
где N — расчетное число циклов; [N] — допускаемое число циклов при вероятности разрушения Pf = 2,3%; N50 — число циклов по формуле (6.197) при заданном значении опа50; jN — коэффициент безопасности по числу циклов, который может быть вычислен по j с учетом наклона полосы разброса экспериментальных точек в логарифмических координатах:
|
(6.199) |
jN = 0a)A.
|
°Та |
|
°Па |
|
тПа |
|
- + 3 |
|
г 1 і I г II г 1 г 1 - I г 11=!, (6.200) ч[°Та]) V [°Па ]) [°Та ] ' [°Па] V [тПа ]) где индексы: Т — поперечные шву напряжения; П — продольные шву напряжения; а — номинальные амплитудные напряжения от внешней нагрузки; в [ ] указаны допускаемые напряжения в указанном направлении. Расчет повреждаемости D в соответствии с гипотезой о линейном суммировании повреждений производят по формулам: D < [D]; [D] = 0,5 -1,0; (6.201) n AND = £ ANj |
|
При двуосном нагружении сварного соединения предельные номинальные амплитудные напряжения от внешней нагрузки по европейским нормам определяются по формуле 2 / 2 / 2 |
|
N j=1Nf, і |
|
°Та • °Па |
Здесь D — полная поврежденность; [D] — допускаемая (permissible) полная поврежденность; ANj — количество циклов с j-м уровнем напряжений; Nf, j — разрушающее количество циклов при j-м уровне напряжений по кривой допускаемых напряжений; n — полное количество уровней напряжений.