ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ОБЩАЯ ТЕКУЧЕСТЬ У КОНЦЕНТРАТОРА
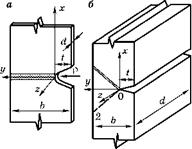
На рис. 6.7 показаны схемы общего течения у концентраторов.
Если толщина пластины d ^ b, и d мало по сравнению с радиусом надреза р (рис. 6.7а), то при растяжении пластины в направлении оси х общее течение происходит в направлении толщины листа в двух плоскостях, наклоненных к оси 2 под углом 45°. Пластическое укорочение в направлении оси у прекращается и возникает состояние плоской деформации с Аву = 0. При этом в минимальном сечении сту = ст2 = стх/2. Напряженное состояние аналогично напряженному состоянию стенки цилиндрического сосуда.
В соответствии с формулой (6.16) максимальную нагрузку можно приближенно оценить как:
|
(6.17) |
Р*,кр = Кв -°В ■ (b - t) ■ d.
|
Рис. 6.7 Зоны пластической деформации у концентратора при общем течении |
На рис. 6.7 б показан концентратор, аналогичный непровару в корне стыкового шва, с размером d » b. В этом случае при общем течении возникают две плоскости сдвига (0-1 и 0-2), наклоненные под 45° к оси у. Однако после потери устойчивости пластических деформаций сдвиг обычно развивается только в одной из этих плоскостей. В среднем по полосе сдвига е2 = 0 и а2 = ст2 = 0,5стж. Металл находит-
ся в состоянии плоской деформации. Поэтому критическая нагрузка, аналогично случаю на рис. 6.7а, может быть приближенно вычислена по формуле (6.17).
Если критическая нагрузка вычисляется по формуле (6.17), то удлинение материала вне пределов концентратора, который находится при одноосном растяжении, связано с нагрузкой Р формулой (6.1). Подставив в эту формулу критическое значение P из формулы (6.17), получим
|
|
где выполнено сокращение на F0 = b ■ d.
Раскрыв в этом уравнении аВ по формуле (6.3) и kaB по формуле (6.16), получим
|
(6.18) |
|
exp(e;) |
|
V3(1+n) |
Для того чтобы решать это уравнение на MathCad, его нужно записать в виде функции. Например:
|
■sl3(1+n) |
|
n n I • exp(n -5), |
|
F(n, tb, 5) = (1 - tb) - |
|
(6.19) |
|
2 |
|
где обозначение деформации растяжения et = e1 = ex в момент раз- Результаты вычислений корней функции (6.19) представлены на рис. 6.8. Так как предельная равномер- |
|
l Ь/п о, |
|
і і і |
^0,20 |
|||
|
m ■ 11 ' ^ |
. 0, |
15 |
||
|
/* |
= 0,1 |
0 |
||
|
L |
ч'А •aKv |
|||
|
~V,: ... |
|
0,4 |
|
о |
|
о |
|
0,2 0,3 0,4 г/6 |
|
Рис. 6.8 Влияние глубины надреза t на относительное удлинение полосы |
|
шкала оси ординат поделена на n. Отложенные по оси ординат отно- Независимо от пластичности фекта. Поэтому в нормах на проектирование допустимую глубину |
|
0,6 |
|
0,2 |
|
0,1 |
|
ной 20% при n = 0,1 снижает относительное удлинение в 10 раз. |